La forza centripeta

Quando un corpo si muove lungo una traiettoria curva, su di esso agiscono delle forze che possono essere scomposte in due componenti principali:

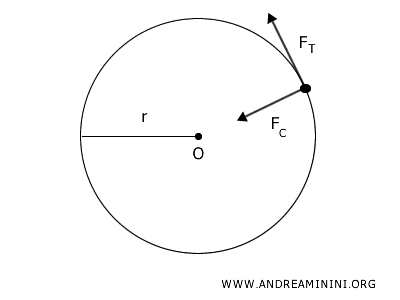
• Forza centripeta \( F_c \)
  La forza che è responsabile del cambiamento di direzione del moto e che mantiene il corpo sulla traiettoria curva è la forza centripeta. La forza centripeta è data da: $$ F_c = m a_c = m v^2 / r $$ dove \( m \) è la massa del corpo, \( v \) è la velocità del corpo, \( r \) è il raggio di curvatura della traiettoria. L'accelerazione $ a = \frac{v^2}{r} $ deriva dal moto circolare.
• Forza tangenziale \( F_T \)
  È tangente alla traiettoria del corpo ed è responsabile della variazione del modulo della velocità del corpo (cioè dell'accelerazione tangenziale). Se \( F_T = 0 \), il modulo della velocità rimane costante e il moto lungo la traiettoria è uniforme, con l'unica accelerazione presente che è quella centripeta \( a_N \).
  

Le forze centripete possono derivare da diverse cause.

Ad esempio, forze di contatto come quelle prodotte da rotaie, pneumatici o fili che collegano il corpo a un punto fisso, oppure forze a distanza come quelle gravitazionali, che agiscono tra corpi senza che ci sia contatto fisico diretto.

Queste forze sono essenziali per mantenere un corpo in movimento lungo una traiettoria curva, contrastando la tendenza del corpo a muoversi in linea retta (secondo la prima legge del moto di Newton).

Un esempio pratico

Un'automobile deve affrontare una curva semicircolare (semicirconferenza).

A quale velocità massima costante può affrontarla senza slittare e uscire di strada?

Analizzo quali forze sono in gioco:

Forza tangenziale \( F_T \)

Quando l'auto sta accelerando o decelerando lungo la curva, si presenta una forza tangenziale \( F_T \) che è responsabile del cambiamento del modulo della velocità.

Ad esempio, se l'auto accelera mentre percorre la curva, il motore dell'auto fornisce una forza tangenziale che aumenta la velocità dell'auto.

In questo caso l'auto mantiene una velocità costante mentre percorre la curva, quindi  \( F_T = 0 \) e l'unica forza in gioco è la forza centripeta.

Forza Normale \( F_N \)

La forza normale \( F_N \) è la forza perpendicolare alla superficie della strada che agisce sull'automobile.

È il risultato della reazione del terreno al peso dell'auto e agisce verticalmente verso l'alto, bilanciando la forza di gravità che agisce verso il basso.

Su una strada piana, questa forza è uguale al peso dell'auto:

$$ F_N = mg $$

Dove \( m \) è la massa dell'auto, mentre \( g \) è l'accelerazione di gravità (circa \( 9.81 \, \text{m/s}^2 \) sulla Terra).

Nota. La forza normale è una forza che agisce perpendicolarmente alla superficie di contatto, come il terreno su cui si muove un oggetto. E' una reazione vincolare. Non è responsabile del cambiamento di direzione del moto, ma piuttosto bilancia la forza di gravità quando il corpo è su una superficie.

Forza di attrito e forza centripeta \( F_C \)

Quando l'auto percorre la curva, le ruote dell'auto esercitano una forza laterale verso l'interno della curva. Questa è la forza centripeta \( F_C \), che mantiene l'auto sulla traiettoria circolare.

Questa forza agisce in orizzontale è dovuta all'attrito tra le gomme dell'auto e la strada.

Per la seconda legge di Newton la forza è F=ma

$$ F_C = m \cdot a $$

Dove $ m $ è la massa del veicolo e $ a $ è l'accelerazione.

Nel caso di un moto circolare uniforme l'accelerazione è $ a = \frac{v^2}{r} $

$$ F_C = m \cdot \frac{v^2}{r} $$

Quindi, la relazione tra la forza centripeta, la massa dell'auto \( m \), la velocità \( v \) e il raggio della curva \( r \) è \( F_C = m \cdot v^2 / r \).

Per non uscire di stada, deve esserci una forza centripeta almeno pari o superiore a $  m \cdot \frac{v^2}{r} $

Ad esempio per un'automobile che affronta una curva su una strada piana, la forza di attrito tra i pneumatici e la strada è quella che genera la forza centripeta necessaria per mantenere il veicolo sulla traiettoria curva.

La forza di attrito dipende dalla forza normale $ F_N $ e dal coefficiente di attrito statico \( \mu_s \):

$$ F_{attrito} = \mu_s F_N $$

Quindi, deve essere soddisfatta la condizione

$$ F_{attrito} \ge F_C $$

$$ \mu_s F_N \geq m \cdot \frac{v^2}{r} $$

Dove $ F_N = mg $

$$ \mu_s m g \geq m \cdot \frac{v^2}{r} $$

$$ \require{cancel} \mu_s \cancel{m} g \geq \cancel{m} \cdot \frac{v^2}{r} $$

$$  \mu_s  g \geq  \frac{v^2}{r} $$

Da questa equazione ricavo la velocità:

$$  v^2 \leq \mu_s  g r  $$

$$ v \leq \sqrt{\mu_s g r} $$

Questa è la velocità massima con cui l'auto può affrontare la curva senza slittare. 

Dalla formula $  v^2 \leq \mu_s  g r  $ che descrive la velocità massima in relazione alla forza di attrito e alla forza centripeta, deduco anche che la velocità massima con cui un oggetto (come un'automobile) può affrontare una curva senza slittare non dipende dalla massa dell'oggetto.

Nota. La forza che fa sembrare che l'auto venga spinta verso l'esterno della curva è la forza centrifuga, che però è una forza apparente percepita all'interno del veicolo. In realtà, quando un'auto esce di strada verso l'esterno della curva, è perché manca una forza centripeta sufficiente a mantenere l'auto nella traiettoria curva. Questa mancanza è dovuta a un'insufficiente attrito tra i pneumatici e la strada.

Esempio di calcolo

Supponiamo che un'automobile abbia una massa di 1000 kg, stia percorrendo la curva a una velocità di 20 m/s e il raggio della curva sia di 50 metri. Il coefficiente di attrito statico tra le gomme e la strada è \( \mu_s = 0.4 \).

Calcolo la forza normale \( F_N \)

$$ F_N = mg = 1000 \text{ kg} \cdot 9.81 \, \text{m/s}^2 = 9810 \, \text{N} $$

Calcolo la forza centripeta \( F_C \) ricordando che $ N = kg \cdot m / s^2 = kg \cdot m \cdot s^{-2} $

$$ F_C = \frac{m \cdot v^2}{r} = \frac{1000 \text{ kg} \cdot 20^2 \ m^2s^{-2}}{50 \ m} \ kg \ m s^{-2}= \frac{1000 \cdot 400}{50} \text{N} = 8000 \, \text{N} $$

Verifico la condizione per evitare slittamento

$$ F_{attrito} = \mu_s F_N = 0.4 \cdot 9810 = 3924 \, \text{N} $$

In questo caso, la forza di attrito (3924 N) non è sufficiente a fornire la forza centripeta necessaria (8000 N), quindi l'auto slitterebbe se affrontasse la curva a 20 m/s.

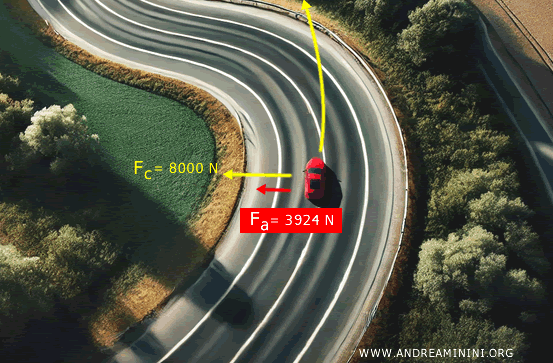
Per evitare lo slittamento, l'auto dovrebbe ridurre la velocità.

Calcolo la velocità massima per affrontare la curva:

$$ v = \sqrt{\mu_s g r} $$

$$ v = \sqrt{0.4 \cdot 9.81 \cdot 50} $$

$$ v = \sqrt{196.2} $$

$$ v = 14 m/s $$

Quindi, la velocità massima a cui l'auto può affrontare la curva senza slittare è circa 14 m/s.

Se la velocità fosse $ v = 14 m/s $ la forza centripeta necessaria per affrontare la curva si ridurrebbe a 3920 N.

$$ F_C = \frac{m \cdot v^2}{r} = \frac{1000 \cdot 14^2}{50} = \frac{1000 \cdot 196}{50} = 3920 \, \text{N} $$

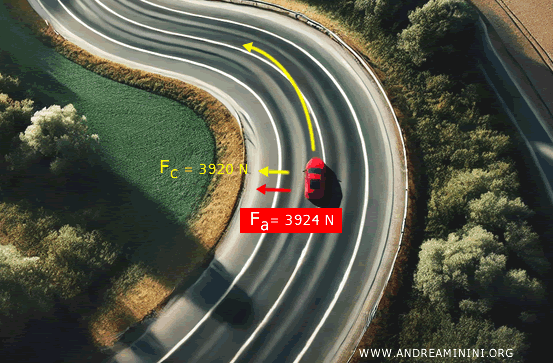
La forza di attrito genererebbe una forza centripeta sufficiente per affrontare la curva.

$$ F_{attrito} = \mu_s F_N = 0.4 \cdot 9810 = 3924 \, \text{N} $$

In questo caso l'autmobile non uscirebbe di strada.

E così via.