Il piano inclinato
La forza di gravità agisce su un corpo posto in un piano inclinato senza attrito facendolo accelerare lungo il piano.
Per semplicità, immagino un corpo simile a un punto materiale di massa m, senza tenere conto di altri aspetti come la forma, le dimensioni, il volume, ecc.
Il piano ha un angolo di inclinazione $ α $.
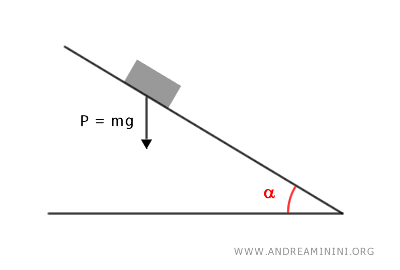
Secondo la legge di Newton $ \vec{F} = m \vec{a} $ che nel caso di un piano inclinato diventa
$$ \vec{P} = \vec{R} + m \vec{a} $$
Dove $ \vec{P} $ è la forza peso mentre $ \vec{R} $ è la reazione vincolare del piano che agisce in direzione opposta.
Questa equazione vettoriale collega il peso del corpo (P), la reazione vincolare del piano (R), la massa (m) e l'accelerazione (a) del corpo.
Scompongo le forze presenti nell'equazione nelle due direzioni: ortogonale (x) e parallela (y) al piano inclinato, sapendo che il peso P=mg è il prodotto per la massa e la gravità.
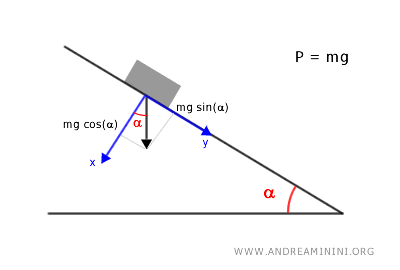
Nella direzione ortogonale (x) la componente del peso è Px=mg·cos(α) mentre la reazione vincolare R del piano inclinato agisce in direzione opposta.
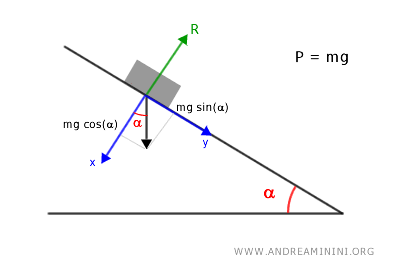
Nella direzione parallela al piano inclinato (y) la componente del peso è Py=mg·sin(α).
$$ \begin{cases} x: \ \ mg \cdot \cos ( \alpha ) = R \\ \\ y: \ \ mg \cdot \sin ( \alpha ) = ma \end{cases} $$
Da notare che l'angolo dell'inclinazione tra le direzioni x e y è congruente con l'angolo di inclinazione del piano perché entrambi gli angoli sono complementari.
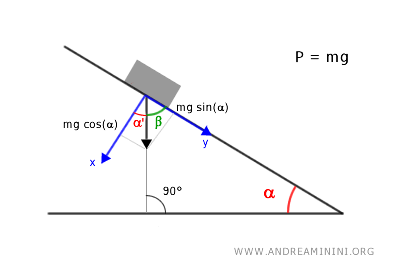
Per semplicità indico momentaneamente l'angolo tra i lati x e y come α'. Gli angoli α'+β=90° sono complementari perché formano un angolo retto tra i lati x e y. $$ \alpha' + \beta = 90° $$ Anche gli angoli interni al triangolo rettangolo α e β sono complementari, perché in un triangolo la somma degli angoli interni è sempre 180° $$ \alpha + \beta +90° = 180° $$ $$ \alpha + \beta = 180°-90° $$ $$ \alpha + \beta = 90° $$ Questo prova che gli angoli α'≅α sono congruenti.
Semplifico il sistema di equazioni
$$ \require{cancel} \begin{cases} x: \ \ mg \cdot \cos ( \alpha ) = R \\ \\ y: \ \ \cancel{m}g \cdot \sin ( \alpha ) = \cancel{m} a \end{cases} $$
La prima equazione mi permette di ottenere la reazione vincolare R=mg·cos(α) del piano inclinato.
La seconda equazione, invece, calcola l'accelerazione a=g·sin(α).
$$ \begin{cases} x: \ \ mg \cdot \cos ( \alpha ) = R \\ \\ y: \ \ g \cdot \sin ( \alpha ) = a \end{cases} $$
Se non c'è attrito, l'accelerazione del corpo è \( g \sin(\alpha) \), dove \( g \) è l'accelerazione di gravità e \( \alpha \) è l'angolo di inclinazione del piano.
$$ a = g \cdot \sin( \alpha ) $$
Questo mi fa capire che il corpo scende lungo il piano inclinato con un moto uniformemente accelerato e che l'accelerazione è minore della gravità (a<g).
Spiegazione. Sapendo che sin(α) è un valore minore o uguale a 1, deduco l'accelerazione del corpo è inferiore alla forza di gravita (a<g) poiché a=g·sin(α)≤g. $$ a = g \cdot \sin( \alpha ) \le g $$
In presenza di attrito statico (\( \mu_s \)) il corpo non si muove a meno che la componente della forza di gravità lungo il piano non superi la forza di attrito.
Quindi, il corpo si muove solo se
$$ mg \cdot \sin( \alpha ) > \mu_s R $$
Dove $ R = mg \cdot \cos ( \alpha ) $
$$ mg \cdot \sin( \alpha ) > \mu_s \cdot mg \cdot \cos ( \alpha ) $$
Pertanto, il corpo si muove solo se l'attrico statico è minore della tangente dell'angolo α.
$$ \frac{ mg \cdot \sin( \alpha ) }{ mg \cdot \cos ( \alpha ) } > \mu_s $$
$$ \frac{ \sin( \alpha ) }{ \cos ( \alpha ) } > \mu_s $$
$$ \tan( \alpha ) > \mu_s $$
Quindi finché $ \tan( \alpha ) < \mu_s $ un corpo fermo resta fermo. Comincia a muoversi solo quando l'angolo $ \alpha $ è sufficientemente ampio da consentire $ \tan( \alpha ) > \mu_s $.
Una volta in movimento la forza di coesione dell'attrito è minore, quindi l'attrito dinamico è inferiore all'attrito statico
$$ \mu_d < \mu_s $$
Questo vuol dire che il moto di un corpo in movimento sul piano inclinato può continuare anche per angolazioni inferiori purché $ \tan( \alpha ) \ge \mu_d $.
Nota. Il moto del corpo è un moto uniformemente accelerato se $ \tan( \alpha ) > \mu_d $. In questo caso la velocità aumenta. Viceversa, il moto è un moto a velocità costante se $ \tan ( \alpha ) = \mu_d $. Quando $ \tan( \alpha ) < \mu_d $ il moto diventa uniformemente decelerato perché il corpo in movimento continua a muoversi ma la velocità si riduce.
Il corpo in moto si ferma solo quando $ \tan( \alpha ) \le \mu_d $
$$ \tan( \alpha ) \lt \mu_d $$
$$ \frac{ mg \cdot \sin( \alpha ) }{ mg \cdot \cos ( \alpha ) } \lt \mu_d $$
$$ mg \cdot \sin( \alpha ) \lt \mu_d \cdot mg \cdot \cos ( \alpha ) $$
Quindi, a differenza del caso di un corpo fermo, un corpo in movimento può continuare a muoversi anche quando l'angolo $ tan( \alpha ) < \mu_d $ perché bisogna considerare la velocità corrente.
In generale, quando il corpo è in movimento è necessario considerare un sistema di equazioni che includa l'effetto frenante $ - \mu_d \cdot R $ dell'attrito dinamico lungo l'asse y.
$$ \require{cancel} \begin{cases} x: \ \ mg \cdot \cos ( \alpha ) = R \\ \\ y: \ \ mg \cdot \sin ( \alpha ) - \mu_d \cdot R = m a \end{cases} $$
Dove $ R = mg \cdot \cos ( \alpha ) $
$$ \begin{cases} x: \ \ mg \cdot \cos ( \alpha ) = R \\ \\ y: \ \ mg \cdot \sin ( \alpha ) - \mu_d \cdot mg \cos(\alpha) = m a \end{cases} $$
$$ \begin{cases} x: \ \ mg \cdot \cos ( \alpha ) = R \\ \\ y: \ \ g \cdot \sin ( \alpha ) - \mu_d \cdot g \cos(\alpha) = a \end{cases} $$
$$ \begin{cases} x: \ \ mg \cdot \cos ( \alpha ) = R \\ \\ y: \ \ g \cdot \left( \sin ( \alpha ) - \mu_d \cdot \cos(\alpha) \right)= a \end{cases} $$
Quindi, l'equazione dell'accelerazione di un corpo in movimento sul piano inclinato considerando l'attrito dinamico è:
$$ a = g \cdot \left( \sin ( \alpha ) - \mu_d \cdot \cos{\alpha} \right) $$
Riassumendo, se l'inclinazione del piano è abbastanza ripida o se l'attrito è sufficientemente basso, il corpo scivolerà lungo il piano. Se invece l'inclinazione non è abbastanza ripida o l'attrito è alto, il corpo resterà fermo.
Un esempio pratico
Considero un corpo di massa \( m = 5 \, \text{kg} \) su un piano inclinato con angolo \( \alpha = 30^\circ \):
L'accelerazione del corpo in assenza di attrito è
$$ a = 9.8 \sin(30^\circ) = 4.9 \, \text{m/s}^2 $$
Introduco l'ipotesi di un attrito statico \(\mu_s = 0.6\)
In questo caso, il corpo resta fermo
$$ \tan(30^\circ) = 0.577 < 0.6 \quad $$
Quando l'attrito statico è elevato, il corpo potrebbe non iniziare a muoversi se l'inclinazione non è sufficiente.
Ora introduco l'ipotesi di un attrito statico a \(\mu_s = 0.5 \) e un attrito dinamico a \( mu_d = 0.4 \)
In questo caso il corpo inizia a muoversi perché $ tan(\alpha) > \mu_s $.
$$ \tan(30^\circ) = 0.577 > 0.5 \quad $$
Una volta superato l'attrito statico, l'attrito dinamico $ \mu_d = 0.4 $ determina l'accelerazione del corpo sul piano inclinato.
$$ a = 9.8 (\sin(30^\circ) - 0.4 \cos(30^\circ)) $$
$$ a = 9.8 (0.5 - 0.4 \cdot 0.866) $$
$$ a = 9.8 (0.5 - 0.3464) $$
$$ a= 9.8 \cdot 0.1536 $$
$$ a = 1.5 \, \text{m/s}^2 $$
In conclusione, la presenza di attrito influenza notevolmente il movimento del corpo.
Questa analisi fornisce un esempio pratico di come un corpo si comporta su un piano inclinato, considerando diversi fattori di attrito e inclinazione.
E così via.
