Pressione
La pressione (p) è una grandezza fisica che misura quanto intensamente una forza agisce su una superficie. E' il rapporto tra la componente perpendicolare della forza $ F_⊥$ e l'area $ A $ della superficie su cui agisce la forza. $$ p = \frac{F_{\perp}}{A} $$
La forza deve essere perpendicolare alla superficie, altrimenti solo la componente normale contribuisce alla pressione.
Se la forza è già perpendicolare, la formula diventa:
$$ p = \frac{F}{A} $$
Osservando la formula si capisce subito che la pressione è direttamente proporzionale alla forza ( F ) e inversamente proporzionale all’area ( A ).
In altre parole, a parità di forza, la pressione aumenta se l’area diminuisce, e diminuisce se l’area aumenta.
Questo vuol dire che per raddoppiare la pressione posso raddoppiare la forza oppure dimezzare l'area. Il risultato finale è lo stesso.
$$ 2p = \frac{2F}{A} = \frac{F}{\frac{A}{2}} $$
Quindi, la stessa forza, applicata su una superficie più piccola, genera una pressione maggiore.
Ad esempio, se tocco un palloncino con un dito la pressione è bassa, perché la forza si distribuisce su una superficie. Il palloncino si deforma ma non si rompe. Se lo tocco con uno spillo con la stessa forza, invece, la pressione diventa elevata, perché la forza è distribuita su una superficie molto più piccola... e il palloncino scoppia.

In altre parole, quando esercito una forza su una superficie, l’effetto dipende non solo dall’intensità della forza, ma anche dall’area su cui è distribuita. Questo spiega perché un palloncino non scoppia se lo premo con un dito, ma scoppia facilmente se lo tocco con uno spillo.
L'unità di misura della pressione
La pressione è una grandezza scalare poiché è rappresentata da un numero che ne indica l'intensità e un'unità di misura.
Nel Sistema Internazionale (SI), l'unità di misura della pressione è il pascal (Pa).
Un pascal equivale a una forza di un newton distribuita su un metro quadrato:
$$ 1 \ \text{Pa} = 1 \ \frac{\text{N}}{\text{m}^2} $$
Questo significa che una pressione di 1 pascal corrisponde all’effetto di una forza di 1 newton esercitata su una superficie di 1 metro quadrato.L'unità di misura della pressione
Il nome "pascal" è in onore del fisico francese Blaise Pascal (1623-1662), che studiò le leggi della pressione nei fluidi.
Nota. Dal punto di vista dimensionale la pressione è il rapporto tra una forza e un'area, ossia una lunghezza (L) al quadrato: \[ p = \frac{[F]}{[L^2]} \] La forza \( F \) ha dimensioni \([M \cdot L \cdot T^{-2}] \), cioè massa × accelerazione. L’area ha dimensioni \([L^2] \). Sostituendo nella formula: \[ [p] = \frac{[M \cdot L \cdot T^{-2}]}{[L^2]} = [M \cdot L^{-1} \cdot T^{-2}] \]
Questa è la dimensione fisica del pascal, che riflette il significato concreto della pressione.
Poiché il pascal è un’unità molto piccola, in pratica si usano spesso multipli come il kilopascal (kPa) o il megapascal (MPa).
La pressione si misura con dispositivi chiamati manometri. Ne esistono di diversi tipi, a seconda del tipo di fluido e del campo di pressione da misurare (aria, gas, liquidi, alta o bassa pressione).
Un esempio di calcolo
Devo determinare la pressione esercitata sulla superficie di un palloncino, se premo con una forza di \( 2.6 \ \text{N} \), utilizzando:
- a) un dito, sapendo che l’area di contatto è \( 1.1 \cdot 10^{-4} \ \text{m}^2 \)
- b) uno spillo, sapendo che l’area della punta è \( 2.1 \cdot 10^{-7} \ \text{m}^2 \)
Inoltre, sapendo che il palloncino scoppia a una pressione di \( 4.1 \cdot 10^{5} \ \text{Pa} \), qual è la forza minima necessaria per far scoppiare il palloncino con uno spillo? Qual è la forza minima con un dito?
a] La pressione esercitata dal dito
Sto esercitando una forza \( F = 2.6 \ \text{N} \) in un'area \( A = 1.1 \cdot 10^{-4} \ \text{m}^2 \) che corrisponde alla superficie del dito.
Quindi, la pressione esercitata con un dito è
\[ p = \frac{F}{A} = \frac{2.6 \ N}{1.1 \cdot 10^{-4} \ m^2} \]
Sapendo che un pascal è $ Pa = \frac{\text{N}}{\text{m}^2} $ e svolgendo i calcoli, ottengo:
\[ p \approx 2.36 \cdot 10^{4} \ \text{Pa} \]
La pressione esercitata con il dito è relativamente bassa perché la forza è distribuita su un’area abbastanza grande.
b] Pressione esercitata con uno spillo
In questo caso sto esercitando una forza \( F = 2.6 \ \text{N} \) in un'area in un'area \( A = 2.1 \cdot 10^{-7} \ \text{m}^2 \) che corrisponde alla punta dello spillo.
Quindi, la pressione esercitata con uno spillo è
\[ p = \frac{F}{A} = \frac{2.6 \ N}{2.1 \cdot 10^{-7} \ m^2 }\]
Sapendo che un pascal è $ Pa = \frac{\text{N}}{\text{m}^2} $ e svolgendo i calcoli, ottengo:
\[ p \approx 1.24 \cdot 10^{7} \ \text{Pa} \]
In questo caso la pressione è enormemente maggiore, perché la stessa forza è concentrata su un’area piccolissima.
c] Qual è la forza minima per far scoppiare il palloncino con lo spillo?
Sapendo che la pressione di rottura del palloncino è \( p = 4.1 \cdot 10^{5} \ \text{Pa} \), uso la definizione di pressione \( p = \frac{F}{A} \) per ricavare la forza:
\[ F = pA \]
Sostituisco il valore della pressione di rottura nella formula e l'area della punta dello spillo \( A = 2.1 \cdot 10^{-7} \ \text{m}^2 \)
\[ F = (4.1 \cdot 10^{5} \ \text{Pa} ) \cdot (2.1 \cdot 10^{-7} \ \text{m}^2 ) \]
Sapendo che un pascal è $ Pa = \frac{\text{N}}{\text{m}^2} $
\[ F = (4.1 \cdot 10^{5} \ \frac{\text{N}}{\text{m}^2} ) \cdot (2.1 \cdot 10^{-7} \ \text{m}^2 ) \]
\[ F = (4.1 \cdot 10^{5} \ \text{N} ) \cdot (2.1 \cdot 10^{-7} ) \]
\[ F = 8.61 \cdot 10^{-2} \ \text{N} \]
Quindi, la forza minima necessaria è:
\( F_{\min} \approx 0.086 \ \text{N} \)
Questa è la forza minima per far scoppiare il palloncino con uno spillo.
d] Qual è la forza minima per far scoppiare il palloncino con un dito?
Il procedimento è sempre lo stesso, dalla definizione della pressione \( p = \frac{F}{A} \) ricavo la forza:
\[ F = pA \]
La pressione di rottura è \( p = 4.1 \cdot 10^{5} \ \text{Pa} \) e l'area premuta dal dito è \( A = 1.1 \cdot 10^{-4} \ \text{m}^2 \)
\[ F = (4.1 \cdot 10^{5} \ \text{Pa}) \cdot (1.1 \cdot 10^{-4} \ \text{m}^2 ) \]
Sapendo che un pascal è $ Pa = \frac{\text{N}}{\text{m}^2} $
\[ F = (4.1 \cdot 10^{5} \ \frac{\text{N}}{\text{m}^2}) \cdot (1.1 \cdot 10^{-4} \ \text{m}^2 ) \]
\[ F = (4.1 \cdot 10^{5} \ \text{N}) \cdot (1.1 \cdot 10^{-4} ) \]
Sommo gli esponenti di 10 \( 10^{5}\cdot 10^{-4} = 10^{1} \) e moltiplico i coefficienti \( 4.1 \cdot 1.1 = 4.51 \)
\[ F = 4.51 \cdot 10^{1} \ \text{N} \]
Quindi, la forza minima necessaria è:
\[ F_{\min} \approx 45 \ \text{N} \]
Questo esempio mostra chiaramente che la pressione non dipende solo dalla forza, ma soprattutto da come è distribuita sulla superficie.
La pressione nei fluidi
La pressione in un fluido è la forza per unità di superficie /data/andreamininiorg/pressione-nei-fluidi-esempio-am-2026-4.gifche il fluido esercita sulle pareti del recipiente che lo contiene, sugli oggetti immersi e sulle altre parti del fluido stesso.
La pressione agisce sempre perpendicolarmente alle superfici su cui è applicata, siano queste le pareti del recipiente, i corpi immersi o superfici ideali all’interno del fluido.
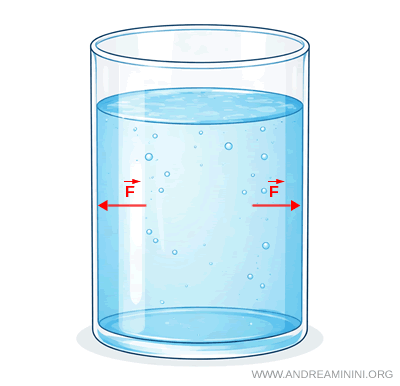
Quando il fluido è in equilibrio, cioè in quiete, la pressione possiede una proprietà fondamentale: in ogni punto del fluido ha lo stesso valore in tutte le direzioni.
Ad esempio, considero un punto qualsiasi all'interno di un fluido in equilibrio e una superficie immaginaria che passa per quel punto. Su ciascun lato della superficie immaginaria agiscono due forze di pressione perpendicolari al piano, uguali in intensità e opposte in verso, che si compensano tra loro.

Se cambio l’orientazione della superficie immaginaria, cambia la direzione della forza esercitata dal fluido, ma il valore della pressione resta invariato. Quindi, la pressione non dipende dall’orientazione della superficie e agisce allo stesso modo in tutte le direzioni.
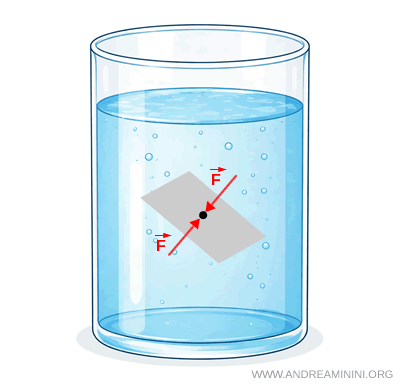
Nota. Poiché la pressione non è associata a una direzione privilegiata, non è una grandezza vettoriale. La pressione è una grandezza scalare.
Di conseguenza, in ogni punto di un fluido in equilibrio agiscono pressioni uguali e opposte in tutte le direzioni.
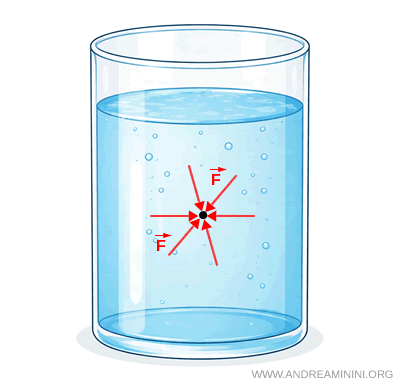
Se questa condizione non fosse soddisfatta, le forze non si compenserebbero, comparirebbe una forza risultante e il fluido inizierebbe a muoversi.
Per questo motivo, l’uguaglianza della pressione in tutte le direzioni è una condizione necessaria per l’equilibrio dei fluidi.
La differenza tra la pressione nei solidi e nei liquidi
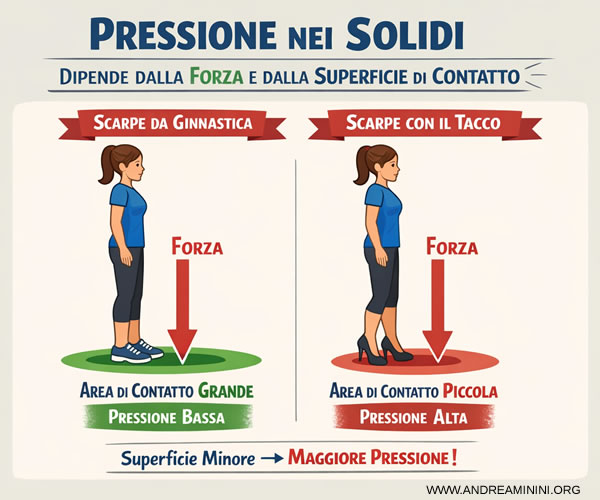
Nei solidi la pressione dipende dalla forza esercitata e dalla superficie di contatto.
Ad esempio, una persona con le scarpe da ginnastica esercita sul terreno una pressione minore rispetto alla stessa persona che indossa scarpe con il tacco, perché l’area di contatto è molto più piccola.
Nei liquidi, invece, la pressione è legata alla profondità. Più si scende in profondità, maggiore è la pressione esercitata dal liquido. Questo avviene perché aumenta il peso della colonna di liquido sovrastante.
Quindi, la pressione in un liquido cresce con la profondità ed è la stessa in tutte le direzioni.

La pressione atmosferica
La pressione atmosferica è la pressione esercitata dall’aria su tutte le superfici a causa del peso della colonna d’aria sovrastante.
L’aria ha una massa e quindi peso. Al livello del mare, la pressione atmosferica normale vale circa:
\[ p_{at} = 1{,}013 \cdot 10^5 \ \text{Pa} \]
Anche se non ce ne accorgiamo, l’atmosfera esercita una forza molto grande su ogni oggetto e su ogni parte del nostro corpo.

Altri esempi
Esempio 1
Una palla con una pressione interna di \( p = 8.0 \times 10^4 \ Pa \) viene lanciata sul pavimento con una forza \( F = 40 \ N \)e rimbalza sul pavimento. Qual è l'area di contatto fra la palla e il pavimento?
Sapendo che la formula della pressione è
$$ p = \dfrac{F}{A} $$
Da questa ricavo la formula inversa dell'area quando è nota la forza e la pressione
$$ A = \dfrac{F}{p} $$
Sostituisco i valori della forza \( F = 40 \ N \) e della pressione \( p = 8.0 \times 10^4 \ Pa \)
$$ A = \dfrac{40}{8.0 \times 10^4} = 5.0 \times 10^{-4} \ m^2 = 5.0 \ cm^2 $$
Pertanto, l'area di contatto è 5 cm2
Qual è il diametro dell’area di contatto?
In questo caso l'areaa è circolare, quindi considero l'area del cerchio
$$ A = \pi \left(\dfrac{d}{2}\right)^2 $$
Da questa ricavo il diametro $ d $
$$ \left(\dfrac{d}{2}\right)^2 = \dfrac{A}{\pi} $$
$$ d = 2 \sqrt{\dfrac{A}{\pi}} $$
Poi sostituisco l'area di contatto
$$ d = 2 \sqrt{\dfrac{5.0 \times 10^{-4}}{\pi}} $$
$$ d = \dfrac{5.0 \times 10^{-4}}{\pi} \approx 1.59 \times 10^{-4} $$
$$ d = \sqrt{1.59 \times 10^{-4}} \approx 0.0126 \ m $$
$$ d \approx 2 \times 0.0126 = 0.0252 \ m = 2.5 \ cm $$
Quindi, il diametro di contatto è circa $ d \approx 2.5 \ cm $
Qual è la pressione totale interna della palla?
La formula della pressione totale è data dalla somma della pressione relativa e di quella atmosferica
$$ p_{tot} = p_r + p_{atm} $$
La pressione della palla \( p = 8.0 \times 10^4 \ Pa \) è quella relativa $ p_r $ (pressione manometrica):
Sapendo che la pressione atmosferica è \( p_{atm} \approx 1.0 \times 10^5 \ Pa \), ottengo la pressione totale.
$$ p_{tot} = 8.0 \times 10^4 \ Pa + 1.0 \times 10^5 \ Pa $$
$$ p_{tot} = 0.8 \times 10^5 \ Pa + 1.0 \times 10^5 \ Pa $$
$$ p_{tot} = 1.8 \times 10^5 \ Pa $$
Quindi, la pressione totale interna è circa 1.8 atm.
E così via.
