Tre vettori linearmente dipendenti sul piano
Dati tre o più vettori sul piano, i vettori sono sempre vettori linearmente dipendenti.
Questo è dovuto al fatto che ogni vettore potrebbe essere calcolato come combinazione lineare degli altri due vettori.
Un esempio pratico
Nel piano R2 ho tre vettori:
$$ v_1 = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \\ v_2 = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ v_3 = \begin{pmatrix} 1 \\ 1 \end{pmatrix} $$
Il vettore v3 è una combinazione lineare di v1 e v2.
$$ v_3 = a_1 v_1 + a_2 v_2 $$
Esistono degli scalari che confermano l'equazione:
$$ a_1 = 1 \\ a_2 = 1 $$
$$ v_3 = 1 \cdot v_1 + 1 \cdot v_2 $$
$$ v_3 = 1 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 1 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$
$$ v_3 = \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix} $$
La rappresentazione cartesiana della combinazione lineare è la seguente:
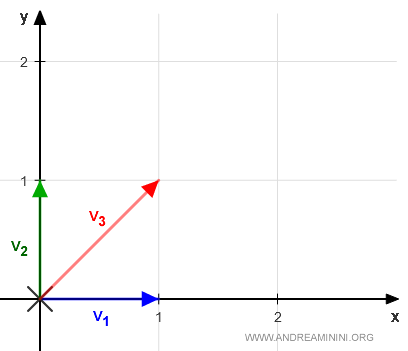
E così via.
