Il punto medio del vettore
Due punti distinti A e B del piano individuano gli estremi del segmento AB. Dato un numero reale alfa compreso tra 0 e 1, esiste un punto C del segmento che lo suddivide in due parti proporzionali α e (1-α).
Questa proprietà è applicabile anche ai vettori.
Dati due punti A e B
$$ A = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} \\ B = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} $$
Questi punti individuano un vettore AB
$$ \overrightarrow{AB} = \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \end{pmatrix} $$
Dato un numero scalare reale alfa, allora esiste un punto C che individua due vettori AC e CB che suddividono il vettore AB in modo proporzionale
$$ \overrightarrow{AC} = α \cdot AB $$ $$ \overrightarrow{CB} = (1-α) \cdot AB $$
Le coordinate del punto C sono le seguenti:
$$ \begin{pmatrix} x_1 - x_c \\ y_1-y_c \end{pmatrix} = α \cdot \begin{pmatrix} x_1 - x_2 \\ y_1-y_2 \end{pmatrix} $$
$$ \begin{pmatrix} x_c - x_2 \\ y_c-y_2 \end{pmatrix} = (1-α) \cdot \begin{pmatrix} x_1 - x_2 \\ y_1-y_2 \end{pmatrix} $$
ossia
$$ \begin{pmatrix} - x_c \\ -y_c \end{pmatrix} = α \cdot \begin{pmatrix} x_1 - x_2 \\ y_1-y_2 \end{pmatrix} - \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} $$
$$ \begin{pmatrix} x_c \\ y_c \end{pmatrix} = (1-α) \cdot \begin{pmatrix} x_1 - x_2 \\ y_1-y_2 \end{pmatrix} + \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} $$
quindi
$$ \begin{pmatrix} x_c \\ y_c \end{pmatrix} = \begin{pmatrix} - α \cdot x_1 + α \cdot x_2 + x_1 \\ - α \cdot y_1 + α \cdot y_2 + y_1 \end{pmatrix} $$
$$ \begin{pmatrix} x_c \\ y_c \end{pmatrix} = \begin{pmatrix} x_1 - x_2 - α \cdot x_1 + α \cdot x_2 + x_2 \\ y_1-y_2 - α \cdot y_1 + α \cdot y_2 + y_2 \end{pmatrix}$$
infine
$$ \begin{pmatrix} x_c \\ y_c \end{pmatrix} = \begin{pmatrix} α x_2 + x_1 (1 - α ) \\ α y_2 + y_1 (1 - α) \end{pmatrix} $$
$$ \begin{pmatrix} x_c \\ y_c \end{pmatrix} = \begin{pmatrix} α x_2 + x_1 (1 - α ) \\ α y_2 + y_1 (1 - α) \end{pmatrix} $$
Un esempio pratico
Dati due punti dello spazio vettoriale R2
$$ A = \begin{pmatrix} 5 \\ 7 \end{pmatrix} \\ B = \begin{pmatrix} 4 \\ 3 \end{pmatrix} $$
Questi punti individuano un vettore AB
$$ \overrightarrow{AB} = \begin{pmatrix} 5 - 4 \\ 7 - 3 \end{pmatrix} = \begin{pmatrix} 1 \\ 4 \end{pmatrix} $$
La rappresentazione grafica del vettore AB è la seguente:
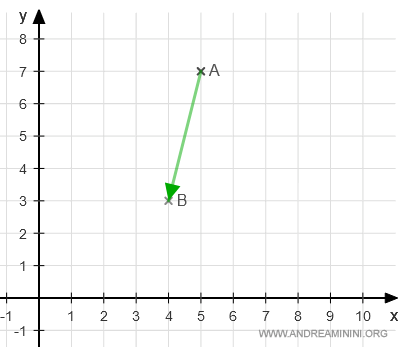
Scelgo uno scalare α compreso tra 0 e 1. Ad esempio, α=0.25.
Esiste un punto intermedio C che individua due vettori AC e CB
$$ \begin{cases} \overrightarrow{AC} = α \cdot AB \\ \overrightarrow{CB} = (1-α) \cdot AB \end{cases} $$
$$ \begin{cases} \overrightarrow{AC} = 0.25 \cdot \begin{pmatrix} 1 \\ 4 \end{pmatrix} \\ \overrightarrow{CB} = (1-0.25) \cdot \begin{pmatrix} 1 \\ 4 \end{pmatrix} \end{cases} $$
$$ \begin{cases} \overrightarrow{AC} = \begin{pmatrix} 0.25 \\ 1 \end{pmatrix} \\ \overrightarrow{CB} = \begin{pmatrix} 0.75 \\ 3 \end{pmatrix} \end{cases} $$
Per trovare il punto intermedio sostituisco i vettori AC e CB con le loro coordinate
$$ \begin{cases} \begin{pmatrix} 5 - x_1 \\ 7 -y_1 \end{pmatrix} = \begin{pmatrix} 0.25 \\ 1 \end{pmatrix} \\ \begin{pmatrix} x_2 - 4 \\ y_2 - 3 \end{pmatrix} = \begin{pmatrix} 0.75 \\ 3 \end{pmatrix} \end{cases} $$
$$ \begin{cases} \begin{pmatrix} - x_1 \\ -y_1 \end{pmatrix} = \begin{pmatrix} 0.25 - 5 \\ 1 - 7 \end{pmatrix} \\ \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} 0.75 +4 \\ 3 + 3 \end{pmatrix} \end{cases} $$
$$ \begin{cases} \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = \begin{pmatrix} 4.75 \\ 6 \end{pmatrix} \\ \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} 4.75 \\ 6 \end{pmatrix} \end{cases} $$
Le coordinate del punto C sono (4.75,6).
La rappresentazione grafica del punto C e dei due vettori AC e CB è la seguente:
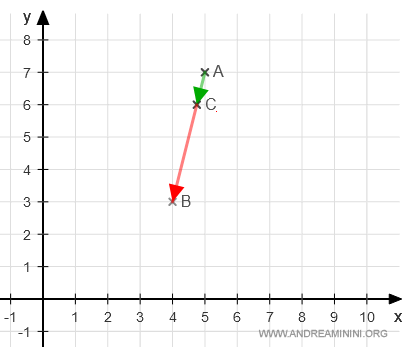
Il punto C suddivide il vettore AB in due vettori proporzionali AC e CB.
E così via.
