La somma di due numeri complessi
La somma di due numeri complessi è molto semplice, basta sommare le parti reali e immaginarie tra loro. $$ (a+bi)+(c+di)=(a+c)+(b+d)i $$
La somma è un numero complesso che ha per parte reale la somma delle parti reali e per parte immaginaria la somma dei coefficienti delle parti immaginarie.
Un esempio pratico
Ho due numeri complessi
$$ z_1 = 2 + 3i $$
$$ z_2 = 5 + 2i $$
Per sommarli associo tra loro le parti reali e immaginarie
$$ z_1 + z_2 = (2 + 3i) + (5 + 2i) $$
$$ z_1 + z_2 = (2 + 5) + (3i + 2i) $$
$$ z_1 + z_2 = 7 + 5i $$
Ho così ottenuto la somma dei due numeri complessi.
Il metodo del parallelogramma
Ogni numero complesso è anche un vettore sul piano di Gauss.
Pertanto, dal punto di vista geometrico posso sommare i due numeri complessi anche sommando i relativi vettori con la regola del parallelogramma.
Un esempio pratico
Rappresento sul piano di Gauss i due numeri complessi z1=2+3i e z2=5+2i.
Al primo numero corrisponde il punto (2,3) mentre al secondo il punto (5,2).
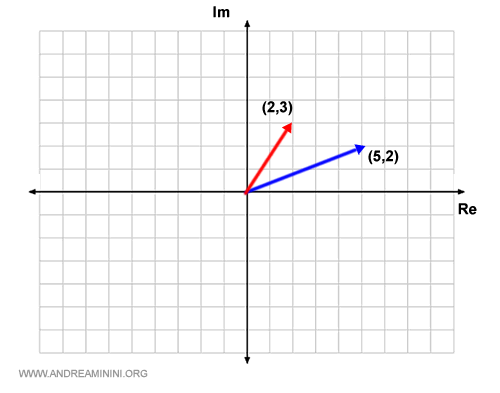
Congiungo l'origine (0,0) con i due punti per rappresentare i due vettori.
Poi sommo i due vettori tra loro con la regola del parallelogramma.
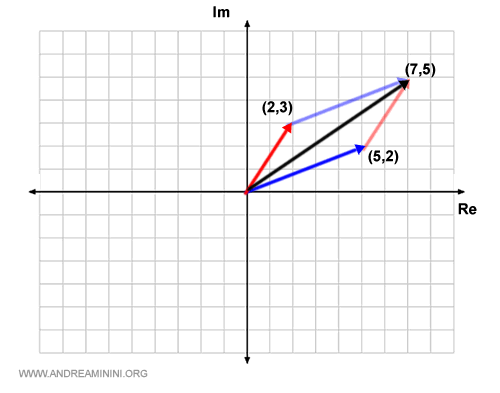
Il vettore somma collega l'origine con il punto del piano (7,5).
Al punto (7,5) del piano di Gauss è associato il numero complesso 7+5i.
E' lo stesso risultato della somma algebrica z1+z2.
E così via.
