Le rette tangenti a una parabola

Data una parabola e un punto qualsiasi P del piano, possono esistere due, una o nessuna retta tangente alla parabola che passa per il punto P.

• Se il punto P è un punto esterno alla parabola, esistono due rette tangenti alla parabola passanti per P.
  
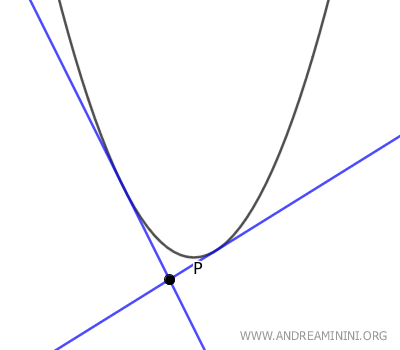
• Se il punto P è un punto della parabola, esiste una sola retta tangente alla parabola che passa anche per P.
  
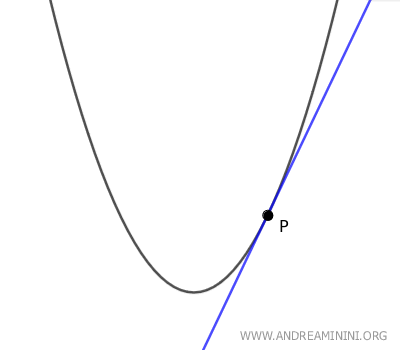
• Se il punto P è un punto interno alla parabola, non esistono rette tangenti alla parabola passanti anche per P.
  

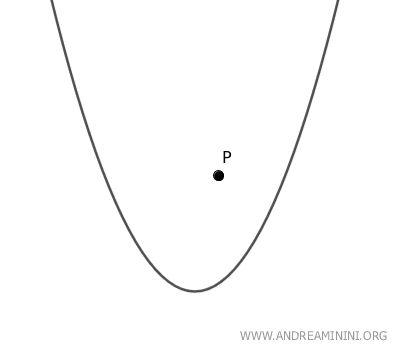
Come trovare le rette tangenti alla parabola

Per determinare quante e quali sono le rette tangenti alla parabola che passano per un punto P, scrivo l'equazione del fascio di rette che passa per il punto \( P(x_0, y_0) \):

$$ y - y_0 = m (x - x_0) $$

Ora devo trovare quali di queste rette hanno punti in comune con la parabola data da:

$$ y = ax^2 + bx + c $$

Quindi, costruisco un sistema di equazioni utilizzando l'equazione del fascio di rette e l'equazione della parabola:

$$ \begin{cases} y - y_0 = m (x - x_0) \\  \\ y = ax^2 + bx + c \end{cases} $$

Le soluzioni di questo sistema rappresentano i punti in comune tra le rette del fascio e la parabola, ovvero le rette tangenti e le rette secanti. 

Per identificare solo le rette tangenti alla parabola, devo imporre anche la condizione di tangenza.

Una retta è tangente a una curva se l'equazione di secondo grado derivante dall'intersezione ha una sola soluzione, cioè due soluzioni coincidenti, il che si verifica quando il discriminante è nullo:

$$ \Delta = b^2 - 4ac = 0 $$

Questa condizione mi permette di determinare il coefficiente angolare \( m \) delle rette tangenti alla parabola.

Una volta trovato il coefficiente angolare \( m \), lo sostituisco nell'equazione del fascio di rette per identificare le rette tangenti.

Un esempio pratico

Considero la parabola con la seguente equazione

$$ y=x^2+2x+3 $$

Devo trovare le rette tangenti alla parabola che passano per il punto P(-1,1).

L'equazione del fascio di rette che passa nel punto P è:

$$ (y-y_0) = m(x-x_0) $$

In questo caso le coordinate del punto P(-1,1) sono x0=-1 e y0=1

$$ (y-1) = m(x-(-1)) $$

$$ (y-1) = m(x+1) $$

Trovo le rette del fascio che hanno punti in comune con la parabola

$$ \begin{cases} y=x^2+2x+3 \\ \\ (y-1) = m(x+1) \end{cases} $$

$$ \begin{cases} y=x^2+2x+3 \\ \\ y = m(x+1) +1 \end{cases} $$

Quindi, l'equazione di 2° grado risolvente del sistema è

$$ x^2+2x+3 = m(x+1)+1 $$

$$ x^2+2x+3 = mx+ m +1 $$

$$ x^2+2x+3 - mx- m -1 $$

$$ x^2+2x- mx- m +2 $$

$$ x^2+x(2-m) +2- m $$

Il discriminante dell'equazione di 2° grado è:

$$ \Delta = b^2-4ac $$

In questo caso i coefficienti sono a=1, b=(2-m) e c=2-m

$$ \Delta = (2-m)^2-4 \cdot 1 \cdot (2-m) $$

$$ \Delta = 4-4m+m^2-8+4m $$

$$ \Delta = m^2-4 $$

Ora impongo la condizione di tangenza $ \Delta = 0 $$

$$ \Delta = m^2-4 = 0 $$

Per trovare i coefficienti angolari (m) delle rette tangenti devo risolvere l'equazione di 2° grado

$$ m^2-4 = 0 $$

Calcolo le soluzioni dell'equazione risolvente:

$$ m = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$

I coefficienti dell'equazione $ m^2-4 = 0 $ sono a=1, b=0 e c=-4

$$ m = \frac{-(0) \pm \sqrt{(0)^2-4 \cdot 1 \cdot (-4)}}{2 \cdot (1)} $$

$$ m = \frac{0 \pm \sqrt{16}}{2} $$

$$ m = \frac{0 \pm 4}{2} $$

$$ m = \begin{cases}  \frac{0 - 4}{2}  = -2 \\ \\  \frac{0+4}{2} = 2 \end{cases} $$

Il sistema ha due soluzioni, quindi ci sono due rette tangenti alla parabola.

I coefficienti angolari delle rette tangenti sono m=-2 e m=2

Li sostituisco nell'equazione del fascio di rette e ottengo le equazioni delle rette tangenti

• Se m=-2 $$ (y-1) = m(x+1) $$ $$ (y-1) = -2(x+1) $$ $$ y = -2x-2+1 $$ $$ y = -2x-1 $$
• Se m=2 $$ (y-1) = m(x+1) $$ $$ (y-1) = 2(x+1) $$ $$ y = 2x+2+1 $$ $$ y = 2x+3 $$

Pertanto, le rette tangenti alla parabola che passano per il punto P(-1;1) sono:

• $ y = -2x-1 $
• $ y = 2x+3 $

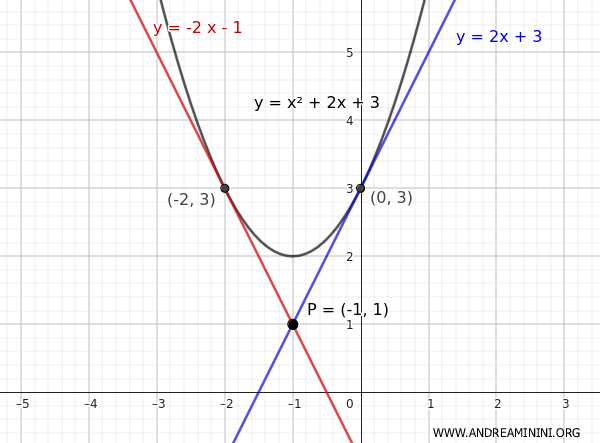
Ecco la rappresentazione grafica della soluzione:

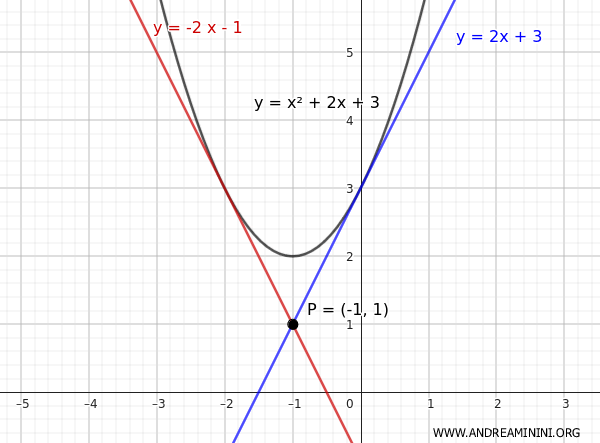
Per trovare le coordinate dei punti di tangenza basta risolvere i sistemi di equazioni composti dall'equazione della retta e della parabola. In questo caso il primo sistema è

$$ \begin{cases} y=x^2+2x+3 \\ \\ y = -2x-1 \end{cases} $$

$$ \begin{cases} -2x-1 =x^2+2x+3 \\ \\ y = -2x-1 \end{cases} $$

$$ \begin{cases}  x^2+4x+4=0 \\ \\ y = -2x-1 \end{cases} $$

L'equazione $ x^2+4x+4=0 $ ha un'unica soluzione $ x = -2 $ perché $ \Delta = 0 $

$$ \begin{cases}  x=-2 \\ \\ y = -2x-1 \end{cases} $$

$$ \begin{cases}  x=-2 \\ \\ y = -2 \cdot (-2) -1 \end{cases} $$

$$ \begin{cases}  x=-2 \\ \\ y = 3 \end{cases} $$

Quindi, un punto di tangenza si trova alle coordinate (-2;3)

Il secondo sistema è:

$$ \begin{cases} y=x^2+2x+3 \\ \\  y = 2x+3 \end{cases} $$

$$ \begin{cases} 2x+3 =x^2+2x+3 \\ \\  y = 2x+3 \end{cases} $$

$$ \begin{cases} x^2=0 \\ \\  y = 2x+3 \end{cases} $$

$$ \begin{cases} x=0 \\ \\  y = 2 \cdot 0+3 \end{cases} $$

$$ \begin{cases} x=0 \\ \\  y = 3 \end{cases} $$

L'altro punto di tangenza si trova alle coordinate (0;3)

E così via.