L'equazione della parabola che passa per due punti ed è tangente a una retta

Per determinare l'equazione di una parabola che passa per due punti dati (x₁, y₁) e (x₂, y₂) e che è tangente a una retta r, posso seguire questi passaggi:

1. Scrivo l'equazione generale della parabola: $$ y = ax^2 + bx + c $$
2. Uso le coordinate dei punti noti (x₁, y₁) e (x₂, y₂) per formare due equazioni:
3. Aggiungo al sistema la condizione di tangenza tra la parabola e la retta r
4. Risolvo il sistema di equazioni per trovare i coefficienti a, b, c dell'equazione della parabola

Un esempio pratico

Una parabola passa per i punti A(2,0) e B(0,1) ed è tangente alla retta 4x+8y-7=0

Devo determinare l'equazione della parabola

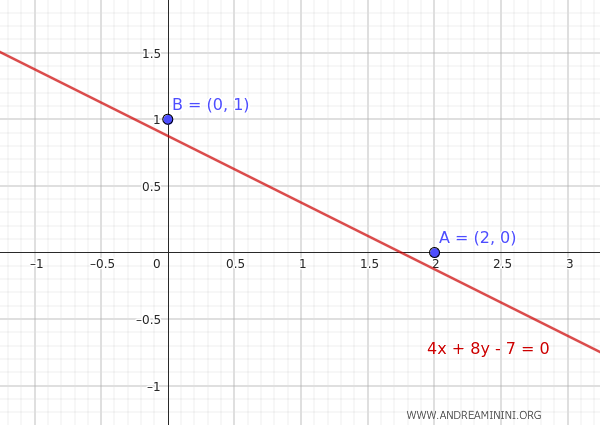
Tuttavia,questi dati iniziali non mi forniscono informazioni sufficienti per capire se la parabola è verticale o orizzontale.

Quindi, devo analizzare entrambe le ipotesi.

1] La parabola è parallela all'asse y

L'equazione di una parabola parallela all'asse y è la seguente:

$$ y = ax^2 + bx + c $$

Come primo passo sostituisco le coordinate dei due punti A(2,0) e B(0,1) per scrivere due equazioni

Per il punto A(2,0) con x₁=2 e y₁=0

$$ y_1 = ax_1^2 + bx_1 + c $$

$$ 0 = a(2)^2 + b(2) + c $$

$$  4a + 2b + c = 0 $$

Per il punto B(0,1) con x₂=0 e y₂=1

$$ y_2 = ax_2^2 + bx_2 + c $$

$$ 1 = a(0)^2 + b(0) + c $$

$$ c = 1 $$

Scrivo un sistema di equazioni

$$ \begin{cases} 4a + 2b + c = 0 \\ \\ c=1 \end{cases} $$

Al sistema devo aggiungere anche la condizione che la parabola sia tangente alla retta 4x+8y-7=0

Scrivo l'equazione della retta in forma esplicita

$$ y = -\frac{4x}{8}+ \frac{7}{8} $$

$$ y = -\frac{x}{2}+ \frac{7}{8} $$

Poi eguaglio l'equazione della retta e l'equazione della parabola per trovare i punti in comune

$$ ax^2 + bx + c = -\frac{x}{2}+ \frac{7}{8} $$

$$ ax^2 + bx + c  + \frac{x}{2}- \frac{7}{8} = 0 $$

$$ ax^2 + (b+\frac{1}{2}) x + c - \frac{7}{8} = 0 $$

Questa equazione di secondo grado individua i punti secanti o tangenti tra la retta e la parabola.

Per trovare solo quelli tangenti devo aggiungere la condizione di tangenza, ovvero il discriminante dell'equazione deve essere nullo $ \Delta = 0 $.

$$ \Delta =(b+\frac{1}{2})^2 - 4 \cdot a \cdot (c- \frac{7}{8}) = 0 $$

$$ \Delta =b^2 + 2 \cdot \frac{1}{2} b + \frac{1}{4} - 4ac + \frac{7a}{2} = 0 $$

$$ \Delta =b^2 + b + \frac{1}{4} - 4ac + \frac{7a}{2} = 0 $$

Aggiungo la condizione di tangenza nel sistema di equazioni.

$$ \begin{cases} 4a + 2b + c = 0 \\ \\ c=1 \\ \\ b^2 + b + \frac{1}{4} - 4ac + \frac{7a}{2} = 0 \end{cases} $$

Quindi, risolvo il sistema per trovare i coefficienti a, b, c della parabola

$$ \begin{cases} 4a + 2b + 1 = 0 \\ \\ c=1 \\ \\  b^2 + b + \frac{1}{4} - 4a + \frac{7a}{2} = 0 \end{cases} $$

$$ \begin{cases} 4a + 2b + 1 = 0 \\ \\ c=1 \\ \\ b^2 + b + \frac{1}{4} - \frac{1}{2}a) = 0 \end{cases} $$

$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c=1 \\ \\ b^2 + b + \frac{1}{4} - \frac{1}{2}a = 0 \end{cases} $$

$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c=1 \\ \\ b^2 + b + \frac{1}{4} - \frac{1}{2} \cdot \frac{-2b - 1}{4} = 0 \end{cases} $$

$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c=1 \\ \\ b^2 + b + \frac{1}{4} + \frac{2b + 1}{8} = 0 \end{cases} $$

$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c=1 \\ \\ b^2 + b + \frac{1}{4} + \frac{b}{4} + \frac{1}{8} = 0 \end{cases} $$

$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c=1 \\ \\ b^2 + \frac{4b+b}{4} + \frac{2+1}{8} = 0 \end{cases} $$

$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c=1 \\ \\ b^2 + \frac{5b}{4} + \frac{3}{8} = 0 \end{cases} $$

$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c=1 \\ \\ b^2 + \frac{5}{4}b + \frac{3}{8} = 0 \end{cases} $$

La terza equazione è di secondo grado è ha come discriminante

$$ \Delta =( \frac{5}{4})^2 - 4 \cdot 1 \cdot \frac{3}{8} $$

$$ \Delta =\frac{25}{16} -  \frac{12}{8} $$

$$ \Delta =\frac{25-24}{16} $$

$$ \Delta =\frac{1}{16} $$

Quindi le soluziono sono

$$ b = \frac{ - \frac{5}{4} \pm \sqrt{ \frac{1}{16} } }{2} $$

$$ b = \frac{ - \frac{5}{4} \pm \frac{1}{4}  }{2} = \begin{cases}  \frac{-1}{2} = - \frac{1}{2} \\ \\  \frac{- \frac{6}{4}}{2} = - \frac{6}{8} = - \frac{3}{4}  \end{cases}   $$

Pertanto le equazioni del sistema sono:

$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c=1 \\ \\  b =  \begin{cases}  - \frac{1}{2} \\ \\    - \frac{3}{4}  \end{cases}   \end{cases} $$

Quindi ci sono due possibili soluzioni:

• Se $ b = - \frac{1}{2}  $  allora $ a = \frac{-2 \cdot (- \frac{1}{2} ) - 1}{4} = \frac{+1 - 1}{4} = 0 $ In questo caso i coefficienti della parabola sono $ a=0 $ . $b = - \frac{1}{2} $ , $ c = 1 $. Tuttavia, questa soluzione va però esclusa perché il coefficiente $ a=0$ non può essere nullo in una parabola.
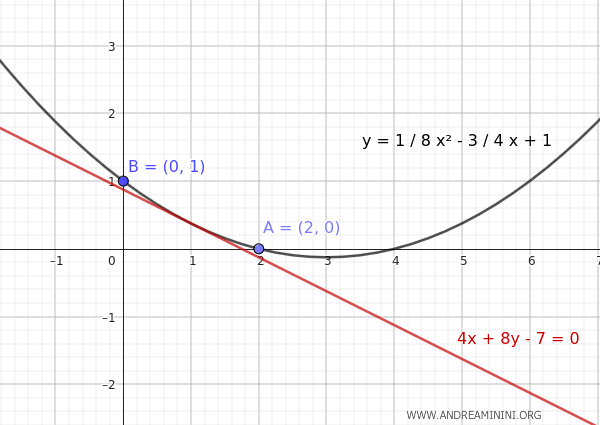
• Se $ b = - \frac{3}{4} $ allora $ a = \frac{-2 \cdot (- \frac{3}{4}) - 1}{4} = \frac{  \frac{3}{2} - 1 }{4} =  \frac{1}{8}  $ In questo caso i coefficienti della parabola sono $ a= \frac{1}{8} $ , $ b = - \frac{3}{4} $, $ c = 1 $. Quindi, l'equazione della parabola è $$ y = ax^2 + bx + c $$ $$ y = \frac{1}{8}x^2 - \frac{3}{4} x + 1 $$ Ecco la rappresentazione grafica. La parabola è tangente alla retta 4x+8y-7=0 e passa per i punti dati A(2,0) e B(0,1).
  

Nota. In alternativa, per trovare la condizione di tangenza potrei scrivere l'equazione della retta in forma esplicita è  $$ y = -\frac{x}{2}+ \frac{7}{8} $$ Quindi, il coefficiente angolare della retta è $ - \frac{1}{2} $. Sapendo che in un punto di tangenza la pendenza tra una curva e una retta è la stessa, potrei calcolare la derivata della parabola che rappresenta la sua pendenza e trovare i valori che la rendono uguale a quella della retta.  La derivata della parabola \(y = ax^2 + bx + c\) è: $$ y' = 2ax + b $$ Pertanto, la condizione di tangenza \(y' = 2\) per punto di tangenza è $$ 2ax + b = 2 $$ $$ b = 2 - 2ax $$ In questo caso il sistema da risolvere è  $$ \begin{cases} 4a + 2b + c = 0 \\ \\ c=1 \\ \\ b = 2 - 2ax \end{cases} $$ La soluzione finale è sempre la stessa. In questo caso però appare anche la variabile x e i calcoli potrebbero essere più lunghi.

2] La parabola è parallela all'asse x

L'equazione di una parabola parallela all'asse x è la seguente:

$$ x = ay^2 + by + c $$

Sostituisco le coordinate dei due punti A(2,0) e B(0,1) nell'equazione:

Per il punto A(2,0) con x₁=2 e y₁=0

$$ x_1 = ay_1^2 + by_1 + c $$

$$ 2 = a(0)^2 + b(0) + c $$

$$  c=2 $$

Per il punto B(0,1) con x₂=0 e y₂=1

$$ x_2 = ay_2^2 + by_2 + c $$

$$ 0 = a(1)^2 + b(1) + c $$

$$ a+b+c = 0 $$

Scrivo le due equazioni in un sistema di equazioni

$$ \begin{cases} c = 2 \\ \\ a+b+c=0 \end{cases} $$

Ora devo aggiungere al sistema la condizione di tangenza tra la parabola e la retta 4x+8y-7=0

Riscrivo l'equazione della retta in questa forma

$$ x = \frac{ 7 - 8y}{4} $$

$$ x = \frac{ 7}{4} - 2y $$

L'equazione della retta e l'equazione della parabola hanno punti in comune (secanti o tangenti) quando:

$$ ay^2 + by + c = \frac{ 7}{4} - 2y $$

$$ ay^2 + by + c - \frac{ 7}{4} + 2y = 0 $$

$$ ay^2 + (b+2)y + c - \frac{ 7}{4} = 0 $$

Questa equazione individua anche i punti secanti ma in questo caso a me interessano solo i punti di tangenza.

Nei punti di tangenza il discriminante dell'equazione di 2° grado $ ay^2 + (b+2)y + c - \frac{ 7}{4} = 0 $ è nullo $ \Delta = 0 $

$$ \Delta = (b+2)^2- 4 \cdot a \cdot ( c - \frac{ 7}{4} ) = 0 $$

Quindi, aggiungo quest'ultima al sistema di equazioni

$$ \begin{cases} c = 2 \\ \\ a+b+c=0 \\ \\  (b+2)^2- 4 \cdot a \cdot ( c - \frac{ 7}{4} ) = 0 \end{cases} $$

A questo punto risolvo il sistema per trovare i coefficienti a, b, c.

$$ \begin{cases} c = 2 \\ \\ a+b+2=0 \\ \\  (b+2)^2- 4 \cdot a \cdot ( 2 - \frac{ 7}{4} ) = 0 \end{cases} $$

$$ \begin{cases} c = 2 \\ \\ a+b+2=0 \\ \\  b^2+4b+4- 4 \cdot a \cdot ( \frac{ 8-7}{4} ) = 0 \end{cases} $$

$$ \begin{cases} c = 2 \\ \\ a=-2-b \\ \\  b^2+4b+4- a = 0 \end{cases} $$

$$ \begin{cases} c = 2 \\ \\ a=-2-b \\ \\  b^2+4b+4- (-2-b) = 0 \end{cases} $$

$$ \begin{cases} c = 2 \\ \\ a=-2-b \\ \\  b^2+4b+4+2+b = 0 \end{cases} $$

$$ \begin{cases} c = 2 \\ \\ a=-2-b \\ \\  b^2+5b+6 = 0 \end{cases} $$

L'equazione di 2° grado $  b^2 +5b+ 6 = 0 $ ha il seguente discriminante

$$ \Delta =(5)^2- 4 \cdot 1 \cdot 6 = 25 - 24 = 1 $$

Quindi, l'equazione ha due soluzioni

$$ b = \frac{ - 5 \pm \sqrt{ 1} }{2}  $$

$$ b = \frac{ - 5 \pm 1 }{2} = \begin{cases}    \frac{-5-1}{2} = -3  \\ \\  \frac{-5+1}{2} = - 2  \end{cases}   $$

Quindi ci sono due possibili soluzioni:

• Se $ b = - 3  $  allora $ a = -2-b = .2- (-3)  = 1  $ In questo caso i coefficienti della parabola sono $ a=1 $ . $ b = -3 $ , $ c = 2 $. Quindi, l'equazione della parabola è $$ x = ay^2 + by + c $$ $$ x = y^2 -3y + 2 $$
• Se $ b = - 2  $  allora $ a = -2-b = -2- (-2)  = 0  $ In questo caso i coefficienti della parabola sono $ a=0 $ . $b = -2 $ , $ c = 2 $. Questa soluzione va però scartata perché una parabola non può avere il coefficiente a=0.

Ecco il grafico della parabola.

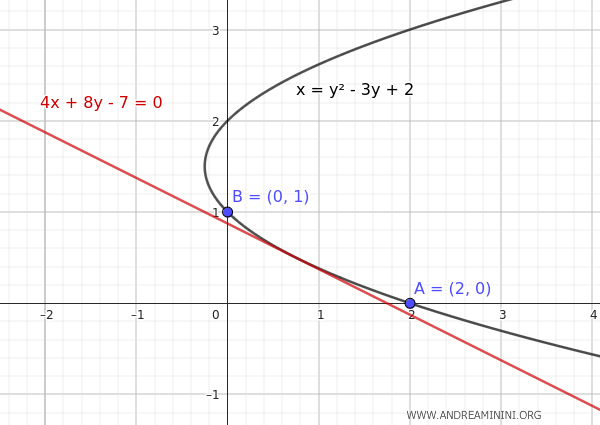
In questo caso la parabola è orizzontale, passa per i punti A(2,0) e B(0,1) ed è tangente alla retta 4x+8y-7=0.

E così via.