La traslazione
La traslazione è una trasformazione geometrica (isometria) che sposta tutti i punti di una figura di una distanza uniforme, nella stessa direzione e verso, lungo la stessa retta specifica.
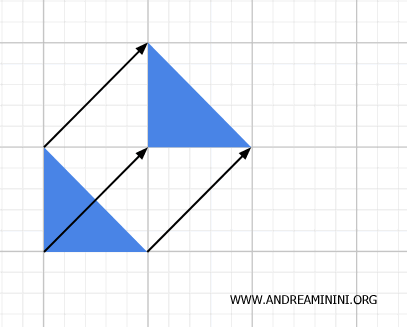
Lo spostamento è rappresentato da vettori noti come "vettori di traslazione". La loro lunghezza, o modulo, corrisponde alla distanza percorsa durante la traslazione.
La direzione del vettore indica la direzione dello spostamento, mentre la punta della freccia ne determina il verso.
La direzione e il verso sono due concetti distinti. Mentre la direzione indica la retta in cui avviene il movimento (es. orizzontale, verticale, obliquo, ecc. ), il verso ne specifica l'orientamento. Ad esempio, un oggetto che si muove orizzontalmente può andare sia a destra sia a sinistra. La direzione è la retta orizzontale. Il verso, invece, indica se si sposta a destra o a sinistra.
In geometria, una traslazione sul piano è rappresentata da una coppia di numeri (x;y):
- Il primo valore "x" denota lo spostamento orizzontale. Per convenzione, verso destra se è positivo, e verso sinistra se è negativo.
- Il secondo valore "y" specifica lo spostamento verticale. Per convenzione, verso l'alto se è positivo e verso il basso se è negativo.
In altre parole, i due numeri della coppia rappresentano la scomposizione dello spostamento di un oggetto sul piano lungo l'asse orizzontale (x) e verticale (y).
I termini x e y sono i componenti dello spostamento.
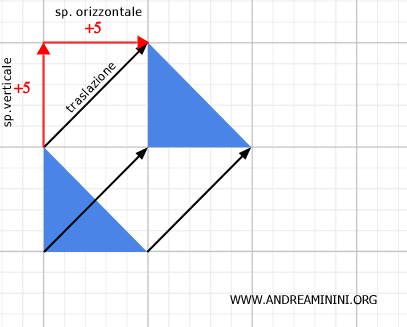
Una figura geometrica, una volta traslata, resta comunque congruente all'originale, perché mantiene inalternata la sua forma e le sue dimensioni.
Dopo la traslazione la distanza tra due punti qualsiasi della figura è sempre la stessa.
Pertanto, la traslazione è un particolare tipo di isometria.
Nota. La traslazione può essere definita anche come la trasformazione geometrica che fa corrispondere a ogni punto $ P $ del piano un punto $ P' $ del piano, tale che il vettore $ \vec{PP'} $ è uguale allo stesso vettore di traslazione $ \vec{v} $. $ \vec{PP'} = \vec{v} $
Le equazioni della traslazione
Le equazioni che descrivono una traslazione sono formulate in termini delle componenti x e y dello spostamento.
$$ \begin{cases} x' = x_0 + x \\ \\ y' = y_0 + y \end{cases} $$
Dove x′ e y′ rappresentano le nuove coordinate, mentre x e y indicano lo spostamento rispetto alle coordinate originali x0 e y0.
Esempio
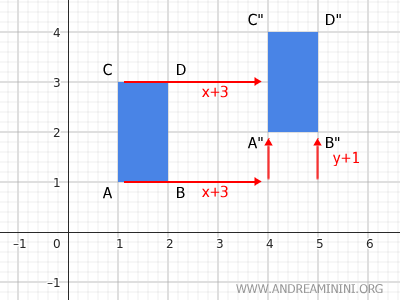
Il rettangolo ABCD ha i suoi vertici alle coordinate A(1;1), B(2;1), C(1;3) e D(2;3) del piano.
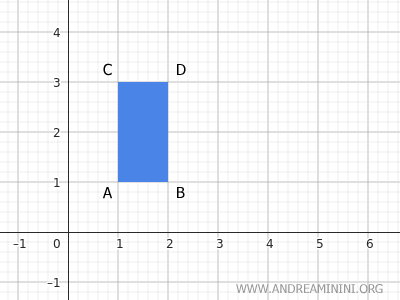
Considero una traslazione (3;1) composta da x=3 passi in orizzontale verso destra e y=1 passi in verticale verso l'alto.
Applico la traslazione in orizzontale +3 alla componente x di ogni punto della figura:
$$ \begin{cases} A'(1+3;1) \\ B'(2+3;3) \\ C'(1+3;3) \\ D'(2+3;3) \end{cases} $$
$$ \begin{cases} A'(4;1) \\ B'(5;2) \\ C'(4;1) \\ D(5;2) \end{cases} $$
In questo modo la figura si sposta verso destra.
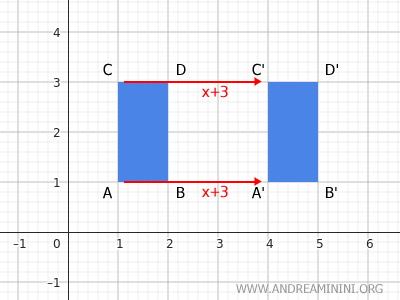
Le frecce di colore rosso sono i vettori dello spostamento per la componente x (orizzontale).
Ogni punto della figura viene spostato in orizzontale della stessa misura. In questo caso, ogni punti viene spostato di 3 posizioni verso destra.
Cos'è un vettore? Un vettore è una grandezza caratterizzata da una lunghezza/intensità, detta modulo, una direzione e un verso. La coda del vettore indica il punto di origine mentre la freccia quello di destinazione.

Ad esempio, il vettore che ha origine dal punto A al punto A' si dice "vettore applicato al punto A". Nel caso della traslazione lo stesso vettore è applicato a tutti i punti della figura geometrica.
Poi eseguo la traslazione +1 della componente verticale, spostando verso l'alto i punti A', B', C', D' della figura.
$$ \begin{cases} A'(4;1+1) \\ B'(5;2+1) \\ C'(4;1+1) \\ D(5;2+1) \end{cases} $$
$$ \begin{cases} A'(4;2) \\ B'(5;3) \\ C'(4;2) \\ D(5;3) \end{cases} $$
Queste ultime sono le coordinate finali della figura dopo la traslazione.
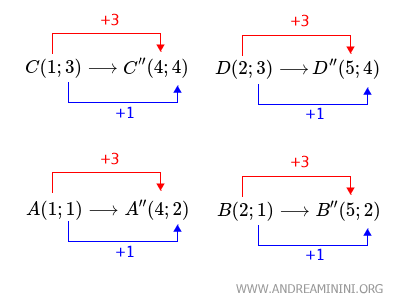
In altre parole, alle coordinate (x;y) di ciascun punto della figura ho sommato algebricamente le componenti (x;y) dello stesso vettore v(3;1).
La traslazione di una funzione
La traslazione di una funzione $ y=f(x) $ consiste nello spostare ogni punto della curva, secondo un vettore $ \vec{v}=(a,b) $ mantenendo invariata la sua forma. $$ y' = f(x' - a) + b $$
Se la funzione di partenza è $y = f(x)$ traslare significa modificare le coordinate di tutti i punti secondo un vettore $ \vec{v}=(a,b) $, ovvero: $$ \begin{cases} x' = x + a \\ y' = y + b \end{cases} $$
Per ottenere la nuova espressione della funzione traslata, ricavo le coordinate originali in funzione di quelle nuove:
$$ \begin{cases} x = x' - a \\ y = y' - b \end{cases} $$
Sostituisco ora queste espressioni nella funzione originale $y = f(x)$:
$$ y' - b = f(x' - a) $$
$$ y' = f(x' - a) + b $$
Questa è la forma generale della funzione traslata.
La curva viene spostata di $ a $ unità lungo l’asse x e di $ b $ unità lungo l’asse y.
Casi particolari
Ci sono due casi particolari
- Traslazione verticale (solo sull’asse y)
Se voglio traslare la funzione solo in verticale, pongo $a = 0$: $$ y' = f(x) + b $$ - Traslazione orizzontale (solo sull’asse x)
Se invece la traslazione è solo orizzontale, imposto $b = 0$: $$ y' = f(x - a) $$
Esempio
Considero la funzione quadratica:
$$ y = 3x^2 $$
Voglio traslarla secondo il vettore $\vec{4, 5}$, cioè 4 unità verso destra e 5 verso l’alto.
Sostituisco i valori nella formula generale:
$$ y = 3(x - 4)^2 + 5 $$
Questa nuova equazione rappresenta la stessa parabola spostata nel piano cartesiano.
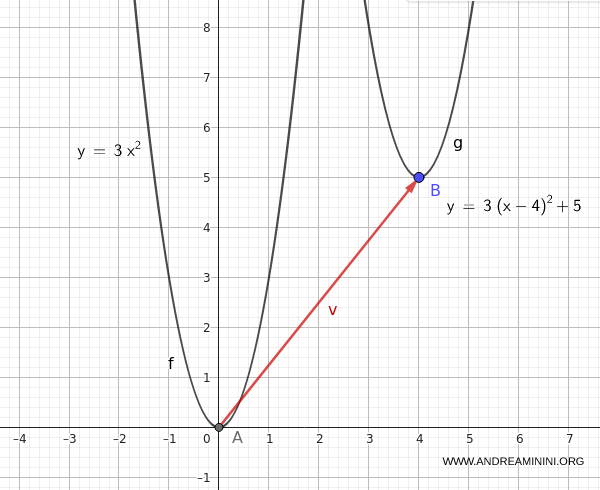
Nota. Questa trasformazione è utile quando si vuole studiare come cambia la posizione di una curva senza alterarne la forma. In altre parole, la funzione non cambia la sua "natura", cambia solo dove si trova.
La traslazione è una isometria
La traslazione è una isometria perché la distanza relativa tra i punti non cambia dopo la trasformazione geometrica.
Dimostrazione
Per dimostrare che una traslazione è una isometria, considero due punti qualsiasi A e B di una figura.
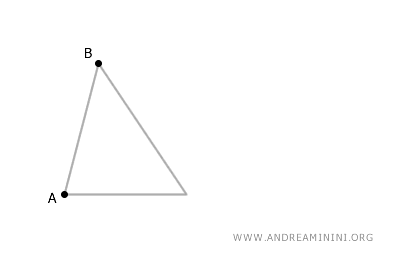
A questi due punti applico lo stesso vettore di traslazione $ \vec{v} $$ e individuo le immagini dei punti A' e B' dopo la trasformazione geometrica.
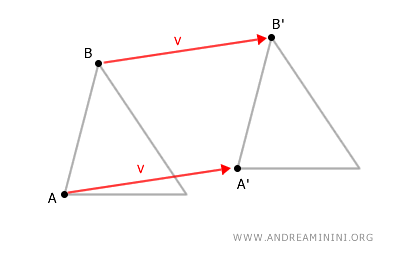
In un'isometria non cambia la distanza tra i punti.
Quindi, devo dimostrare che la distanza tra i punti A' e B' è la stessa tra i punti A e B.
I segmenti AA' e BB' sono congruenti e paralleli, perché ho utilizzato lo stesso vettore di traslazione.
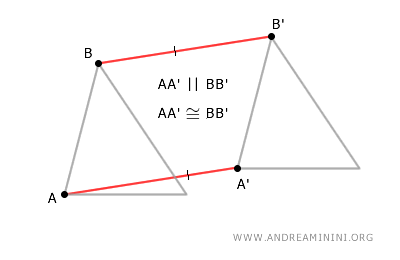
Pertanto, unendo tutti i punti, la figura AA'B'B è un parallelogramma.
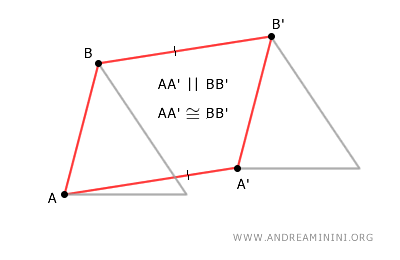
In un parallelogramma tutti i lati opposti sono congruenti e paralleli.
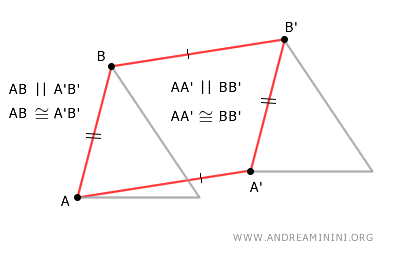
Di conseguenza, anche i segmenti AB e A'B' sono congruenti, ovvero hanno la stessa lunghezza.
$$ \overline{AB} \cong \overline{A'B'} $$
Questo dimostra che la distanza tra i punti A e B e quella tra i punti A' e B' è la stessa.
Pertanto, la traslazione è un'isometria.
La traslazione nello spazio
Una traslazione nello spazio è una trasformazione geometrica che sposta ogni punto di un solido di un vettore \(\vec{v}\), mantenendo inalterate le distanze e gli angoli tra i punti del solido.
Se un punto \( P(x, y, z) \) viene traslato secondo un vettore \( \vec{v} = (a, b, c) \), le sue coordinate dopo la trasformazione diventano:
\[ P'(x', y', z') = (x + a, y + b, z + c). \]
Questo mostra come la traslazione sia una somma vettoriale nelle tre dimensioni.
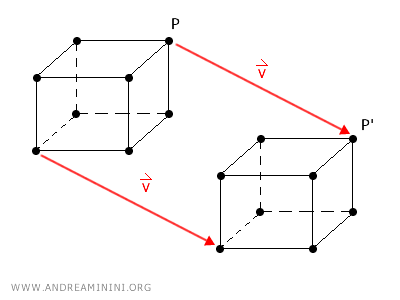
Quindi, la traslazione nello spazio tridimensionale segue esattamente le stesse regole della traslazione nel piano, ma con l'aggiunta della terza dimensione.
Le proprietà della traslazione nello spazio
La traslazione conserva tutte le proprietà metriche della figura solida. Questo garantisce che la figura traslata sia perfettamente congruente a quella originale.
In particolare sono congruenti le lunghezze dei segmenti che rimangono invariate, gli angoli, le relazioni di parallelismo e di allineamento.
Pertanto, anche nello spazio la traslazione è una isometria, ovvero preserva la distanza tra i punti.
Inoltre, è una trasformazione affine, perché mantiene il parallelismo, la collinearità e i rapporti tra segmenti allineati.
Osservazioni
Alcune osservazioni e note a margine sulla traslazione
- La composizione di più traslazioni è ancora una traslazione
La composizione sequenziale di due o più traslazioni è equivalente a un'unica traslazione, il cui vettore è la somma vettoriale dei vettori delle traslazioni originarie. Pertanto, eseguire due o più traslazioni in successione su una figura equivale all'applicazione di una singola traslazione definita dalla combinazione lineare dei vettori di traslazione iniziali.
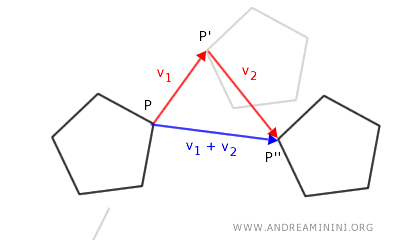
Nella geometria analitica la composizione di due traslazioni di vettori $ \vec{v}_1 $ e $ \vec{v}_2 $ è ancora una traslazione di vettore $ \vec{v}_1 + \vec{v}_2 $
- La proprietà commutativa
La composizione di due traslazioni di vettori $ \vec{v}_1 $ e $ \vec{v}_2 $ soddisfa la proprietà commutativa $ \vec{v}_1 \circ \vec{v}_2 = \vec{v}_2 \circ \vec{v}_1 $ - La traslazione di una retta è sempre una retta parallela oppure coincidente.
Se il vettore di traslazione ha la stessa direzione della retta, in un verso o nell'altro è indifferente, il risultato della traslazione è una retta coincidente.
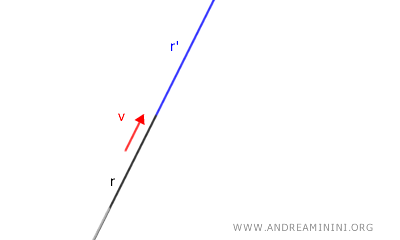
Se, invece, ha una direzione diversa, il risultato è una retta parallela.
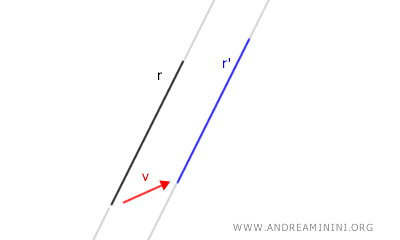
- La traslazione nulla coincide con l'identità
Una traslazione è detta nulla se il vettore di traslazione è un vettore nullo, ovvero un vettore con modulo uguale a zero, direzione e verso indeterminati.$$ \vec{v} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$ Se sommo il vettore nullo a un punto qualsiasi, il risultato è il punto stesso. Le sue coordinate cartesiane non cambiano. $$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$ Pertanto, la traslazione nulla di una figura coincide con la figura stessa. Il risultato è una figura unita. In altre parole è una identità.Cos'è una figura unita? Una figura è detta figura unita se la sua trasformata coincide con la figura stessa. Ad esempio, la traslazione nulla genera una figura unita.
- Traslazione orizzontale o verticale
Le traslazioni orizzontali o verticali sono due casi particolari di traslazione. Se il vettore di traslazione è $ vec{v}(a,0) $ si ha una traslazione orizzontale dei punti, mentre se è è $ vec{v}(0,b) $ si ha una traslazione verticale. - Punti uniti
In una traslazione diversa dall'identità non ci sono punti uniti.Nota. Una traslazione genera una identità se entrambi le componenti del vettore di traslazione sono nulle $ \vec{v}(0,0) $. Se almeno una delle componenti $ \vec{v}(a,b) $ è diversa da zero, ogni punto cambia le proprie coordinate $$ \begin{cases} x' = x+a \\ \\ y' = y+b \end{cases} $$ Quindi, è impossibile che si verifichi un punto fisso nella traslazione.
- Le rette parallele alla traslazione sono globalmente unite
In una traslazione, ogni retta parallela al vettore di traslazione è globalmente unita: l’isometria la trasforma in se stessa, senza però lasciare invariati i singoli punti.

E così via.
