L'equazione di una parabola ruotata con l'asse obliquo
Per ottenere una parabola con vertice \( (h, k) \) e asse di simmetria inclinato di un angolo \(\alpha\) basta ricordare che una parabola con asse inclinato è il risultato di un'operazione isometrica di rotazione.
Ad esempio, se ruoto di un angolo \(-\alpha\) le coordinate di un punto (x,y), ottengo delle nuove coordinate (x',y'):
$$ x' = (x - h) \cos(\alpha) + (y - k) \sin(\alpha) $$
$$ y' = -(x - h) \sin(\alpha) + (y - k) \cos(\alpha) $$
Quindi, se l'equazione della parabola iniziale con asse parallelo all'asse y è:
$$ y = ax^2 $$
La parabola nella nuova coordinate \( (x', y') \) ha l'equazione standard:
$$ y' = a (x')^2 $$
Sostituisco \( x' \) e \( y' \) nell'equazione della parabola $ y' = a (x')^2 $ e ottengo l'equazione ruotata:
$$ -(x - h) \sin(\alpha) + (y - k) \cos(\alpha) = a \left[ (x - h) \cos(\alpha) + (y - k) \sin(\alpha) \right]^2 $$
Se la parabola iniziale è data nella forma canonica con asse verticale, \( (x - h)^2 = 4p(y - k) \), dopo la rotazione di \(\alpha\) l'equazione diventa:
$$ (x' - h)^2 = 4p(y' - k) $$
Sostituisco le coordinate ruotate $ x' $ e $ y' $ e ottengo
$$ \left[(x - h) \cos(\alpha) + (y - k) \sin(\alpha)\right]^2 = 4p \left[-(x - h) \sin(\alpha) + (y - k) \cos(\alpha)\right] $$
Queste sono le equazioni della parabola ruotata.
Nota. Nell'equazione canonica della parabola $ (x' - h)^2 = 4p(y' - k) $ il termine $ p $ è la distanza dal vertice al fuoco. Il coefficiente 4p definisce l'apertura della parabola, dove 4 è una costante che deriva dalle proprietà geometriche della parabola. Per un approfondimento rimando alla dimostrazione dell'equazione canonica della parabola.
Un esempio pratico
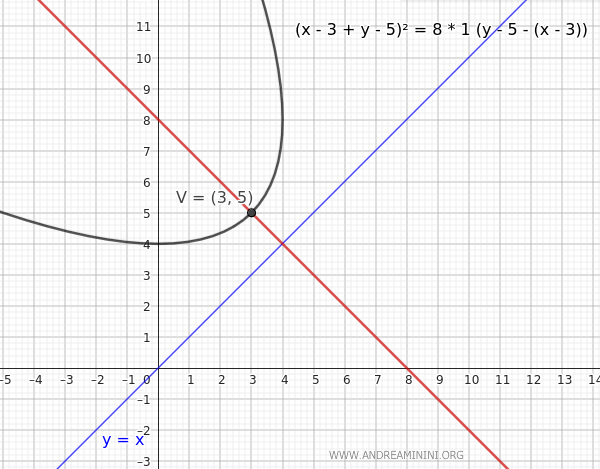
Considero una parabola con vertice in $ V(h,k)=(3,5) $ inclinata con un angolo di 45°, cioè \(\alpha = 45^\circ\) o \(\alpha = \frac{\pi}{4}\):
L'equazione della parabola ruotata è
$$ \left[(x - h) \cos(\alpha) + (y - k) \sin(\alpha)\right]^2 = 4p \left[-(x - h) \sin(\alpha) + (y - k) \cos(\alpha)\right] $$
Sostituisco $ h=3 $ , $ k=5 $ e $ \alpha=45° $
$$ \left[(x - 3) \cos(45°) + (y - 5) \sin(45°)\right]^2 = 4p \left[-(x - 3) \sin(45°) + (y - 5) \cos(45°)\right] $$
Sapendo che $ \cos(45^\circ) = \sin(45^\circ) = \frac{1}{\sqrt{2}} $ l'equazione diventa:
$$ \left[(x - 3) \frac{1}{\sqrt{2}} + (y - 5) \frac{1}{\sqrt{2}}\right]^2 = 4p \left[-(x - 3) \frac{1}{\sqrt{2}} + (y - 5) \frac{1}{\sqrt{2}}\right] $$
Simplifico i termini e ottengo:
$$ \left[(x - 3) + (y - 5)\right]^2 = 8p \left[(y - 5) - (x - 3)\right] $$
Espandendo e semplificando ulteriormente, ottengo l'equazione corretta della parabola ruotata.
E così via.
