Fascio di parabole
Un fascio di parabole è la combinazione lineare di due parabole base dette parabole generatrici del fascio.
Ad esempio, data una parabola generatrice con $ a_1 \ne 0 $ scritta in forma implicita
$$y + a_1 x^2 + b_1 x + c_1 = 0 $$
e una seconda parabola generatrice con $ a_2 \ne 0 $
$$ y + a_2 x^2 + b_2 x + c_2 = 0 $$
un fascio di parabole può essere descritto come:
$$ (y + a_1 x^2 + b_1 x + c_1) + \lambda \cdot (y + a_2 x^2 + b_2 x + c_2) = 0 $$
Dove \(\lambda \in \mathbb{R} \) è un parametro reale.
Al variare di \(\lambda\) si ottengono tutte le parabole del fascio.
Le parabole di un fascio di parabole possono intersecarsi in uno, nessuno o due punti del piano detti punti base del fascio.
Nota. In altre parole, un fascio di parabole è una famiglia di parabole che dipendono da un parametro variabile, e la forma specifica del fascio dipende da come variano i coefficienti dell'equazione quadratica che definisce le parabole. Con $ \lambda = 0 $ ottengo la prima parabola. $$ (y + a_1 x^2 + b_1 x + c_1) + 0 \cdot (y + a_2 x^2 + b_2 x + c_2) = 0 $$ $$ y + a_1 x^2 + b_1 x + c_1 = 0 $$ Non c'è però alcun valore di $ \lambda $ in grado di rappresentare la seconda parabola. Quindi, la combinazione lineare precedente rappresenta tutte le combinazioni fra le due parabole tranne una (la seconda parabola). Per rappresentare anche la seconda parabola dovrei scrivere il fascio di parabole usando due parametri reali anziché uno $$ \lambda_1 \cdot (y + a_1 x^2 + b_1 x + c_1) + \lambda_2 \cdot (y + a_2 x^2 + b_2 x + c_2) = 0 $$ Dove $ \lambda_1 , \lambda_2 \in \mathbb{R} $
In alternativa, il fascio di parabole può anche essere rappresentato in questa forma generale equivalente
$$ (a_1 + \lambda a_2 ) x^2 + (b_1 + \lambda b_2) x + (1 + \lambda ) y + c_1 + \lambda c_2 = 0 $$
Quest'ultima forma è molto utile perché può essere scritta come:
\[ A x^2 + B x + C y + D = 0 \]
Dove nel nostro caso:
$$ A = a_1 + \lambda a_2 $$
$$ B = b_1 + \lambda b_2 $$
$$ C = 1 + \lambda $$
$$ D = c_1 + \lambda c_2 $$
Questo mi permette di trovare le equazioni del vertice e del fuoco usando le formule di una parabola qualsiasi.
- Fuoco
$$ F \begin{pmatrix} - \frac{B}{2A} \ , \ \frac{1-Δ}{4A} \end{pmatrix} $$ - Vertice
$$ V \begin{pmatrix} - \frac{B}{2A} \ , \ - \frac{Δ}{4A} \end{pmatrix} $$ - Direttrice
$$ y= - \frac{1+Δ}{4A} $$ - Asse di simmetria
$$ x= - \frac{B}{2A} $$
Dove A,B,C sono i coefficienti dell'equazione del fascio di parabole y=Ax2+Bx+C e il discriminante è Δ=B2-4AC
Nota. Per essere un fascio di rette, nell'equazione deve esserci sempre la componente quadratica come in qualsiasi parabola. In altre parole, il coefficiente A deve essere non nullo (A≠0).
Un esempio pratico
Considero due parabole generatrici:
$$ p_1: y=x^2−3x+2 $$
$$ p_2: y=−x^2+5x−4 $$
Scrivo entrambe le parabole nella forma implicita
$$ p_1: y-x^2+3x-2=0 $$
$$ p_2: y+x^2-5x+4=0 $$
In questo caso le due parabole generatrici sono secanti perché si intersecano in due punti A(1;0) e B(3;2).
Questi due punti sono anche i punti base del fascio delle parabole.
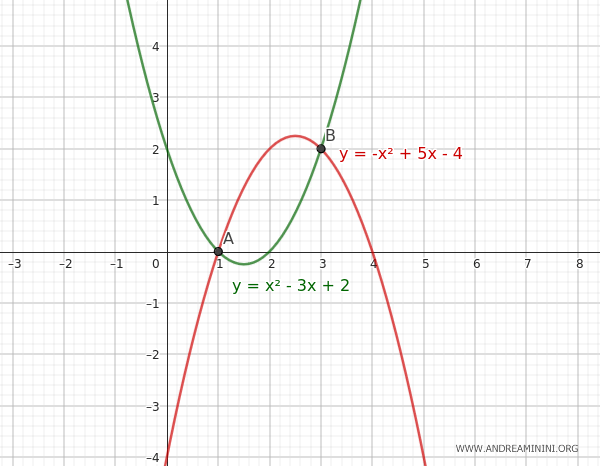
Il fascio di parabole ottenuto dalla combinazione lineare delle due parabole generatrici è
$$ p_1 + \lambda \cdot p_2 = 0 $$
$$ (y-x^2+3x-2) + \lambda \cdot (y+x^2-5x+4) = 0 $$
$$ (\lambda - 1) x^2 + (3-5 \lambda) x + (1+ \lambda) y-2 + 4 \lambda = 0 $$
Al variare del parametro λ ottengo tutte le parabole del fascio di parabole che passano per i punti di intersezione delle parabole.
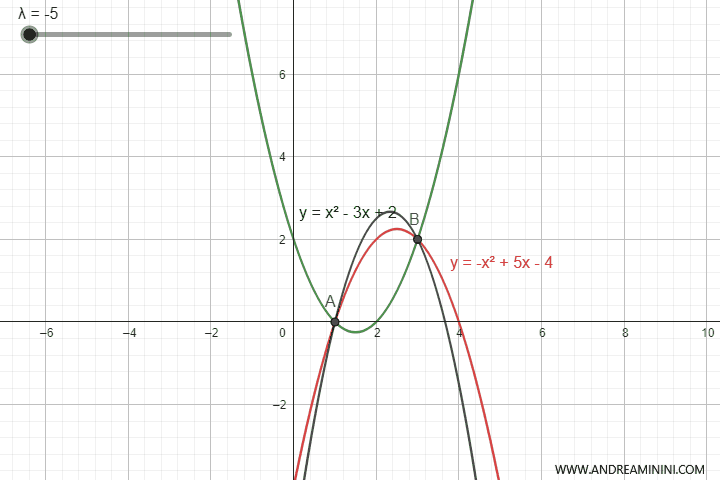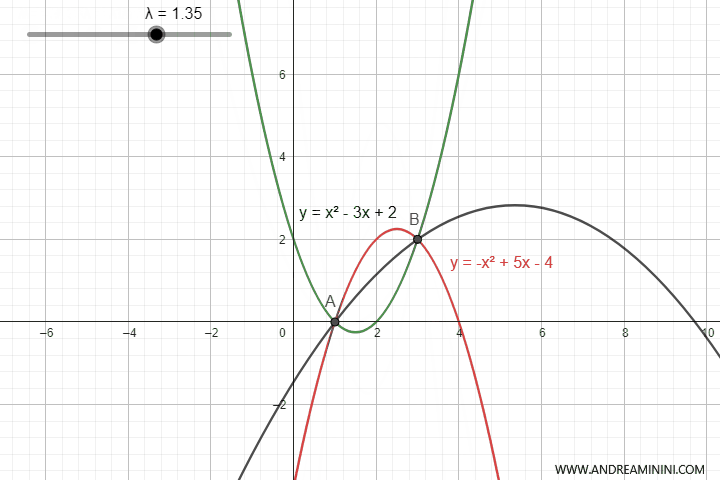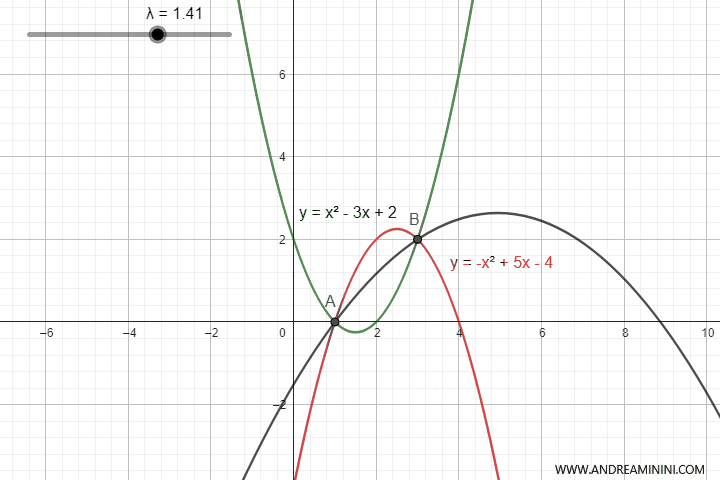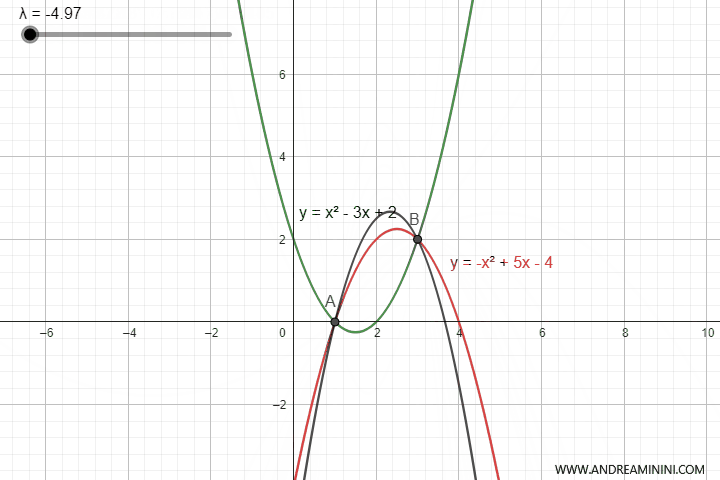
Per ottenere l'equazione del fascio di parabole avrei potuto prendere qualsiasi coppia di parabole del fascio. Anche le parabole degeneri ovvero quelle che in alcuni valori del parametro λ si trasformano in rette.
Esempio. Per trovare le equazioni del fascio di parabole dati posso usare anche le parabole degeneri del fascio. Ad esempio, voglio trovare l'equazione del fascio di due parabole secanti che hanno come punti base A(1,0) e B(3,2). Quando le generatrici sono secanti, due parabole degenerano in due rette. Una parabola degenera in una retta che passa per entrambi i punti base A e B, un'altra parabola degenera in due rette parallele all'asse di simmetria che passano ciascuna in un punto base.
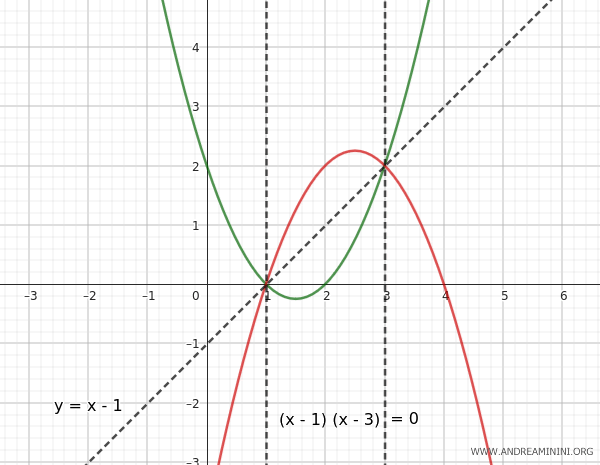
Per trovare il fascio di parabole prendo in considerazione le parabole degeneri. L'equazione della retta che passa per entrambi i punti A(x1,y1)=(1,0) e B(x2,y2)=(3,2) è la seguente
$$ \frac{y-y_1}{y_2-y_1}= \frac{x-x_1}{x_2-x_1} $$
$$ \frac{y-0}{2-0}= \frac{x-1}{3-1} $$
$$ \frac{y}{2}= \frac{x-1}{2} $$
$$ y = x-1 $$
$$ y -x + 1= 0 $$
La seconda parabola ha come radici 1 e 3, quindi è il prodotto delle rette (x-1) e (x-3)
$$ (x-1)(x-3)=0 $$
Quindi, l'equazione del fascio di parabole è la combinazione lineare delle due parabole degeneri
$$ y - x+ 1 + \lambda [ (x-1)(x-3) ]=0 $$
Il risultato finale è sempre lo stesso.Tipi di parabole generatrici
Il fascio di parabole può essere generato da parabole secanti, tangenti, esterne o congruenti con un punto in comune o meno. Per semplicità considero solo il caso delle parabole verticali ossia parallele all'asse y.
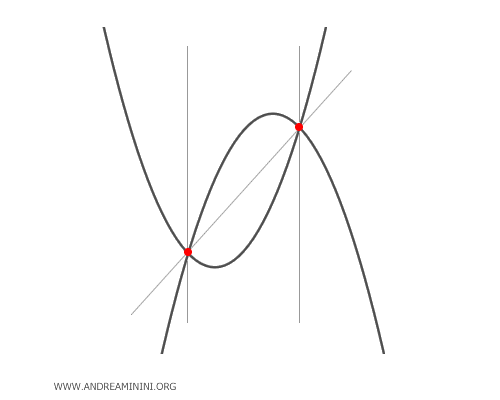
- Le parabole secanti
Le parabole secanti hanno due punti di intersezione che coincidono con i due punti base del fascio di parabole. In alcuni valori del parametro λ la parabola del fascio si trasforma in una retta che passa i punti base ed è detta "parabola degenere".
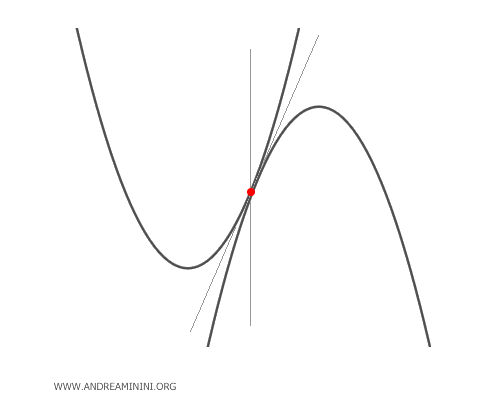
- Le parabole tangenti
Le parabole tangenti hanno un unico punto di intersezione che coincide con il solo punto base del fascio. In alcuni valori del parametro λ la parabola del fascio degenera in una retta che passa per il punto base. In paricolar modo in una retta tangente e in una retta parallela all'asse di simmetria.
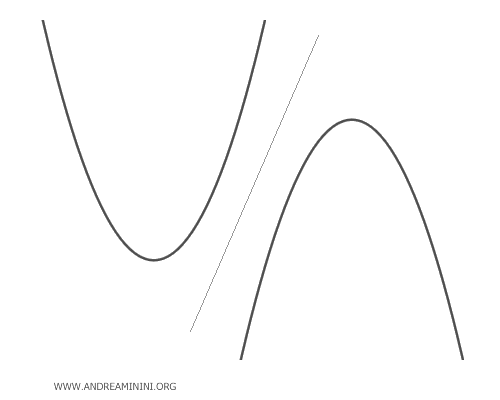
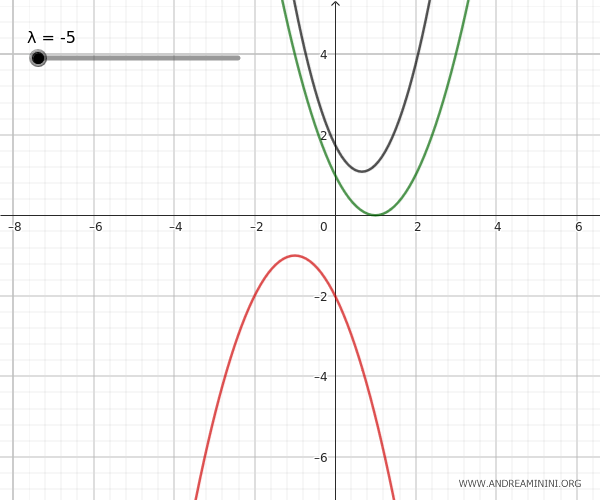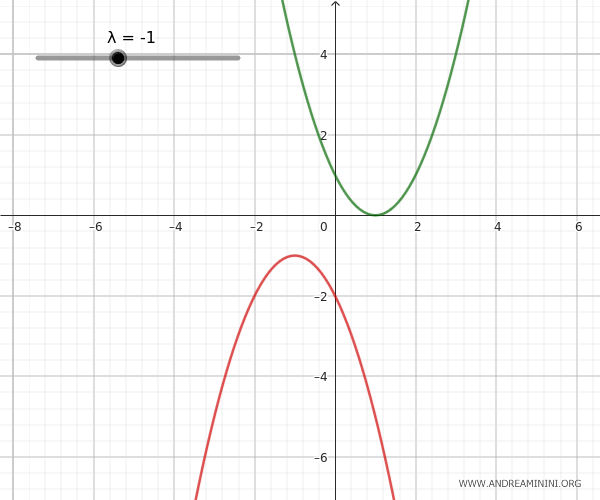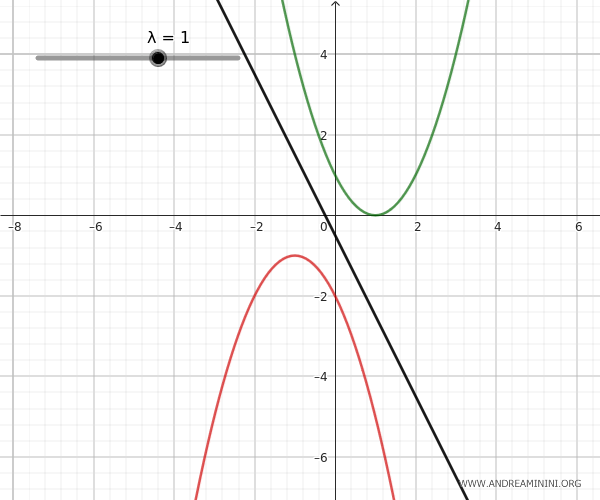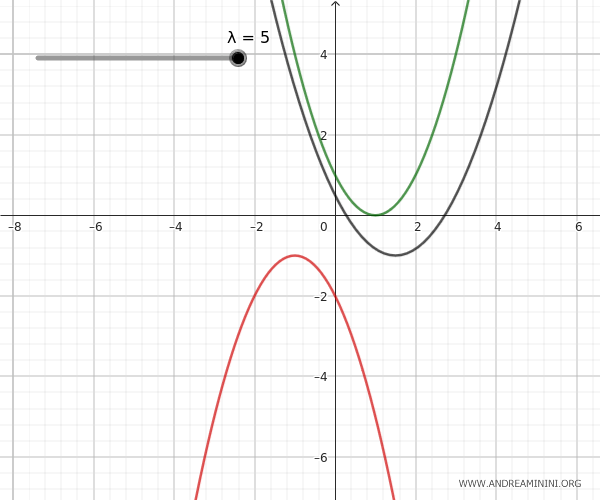
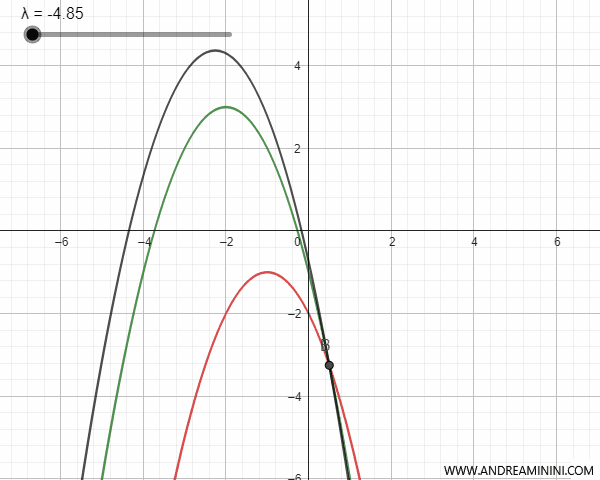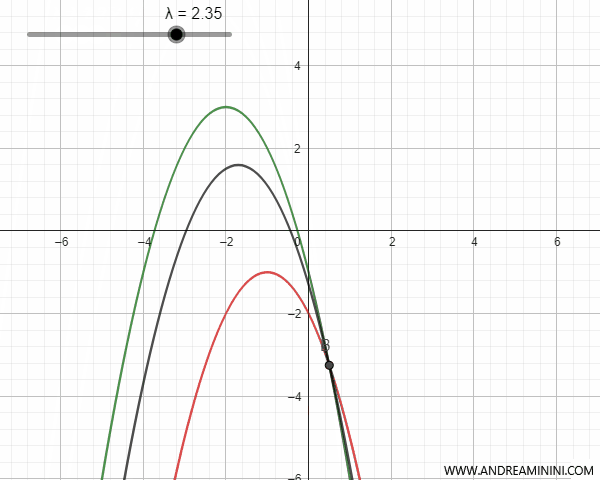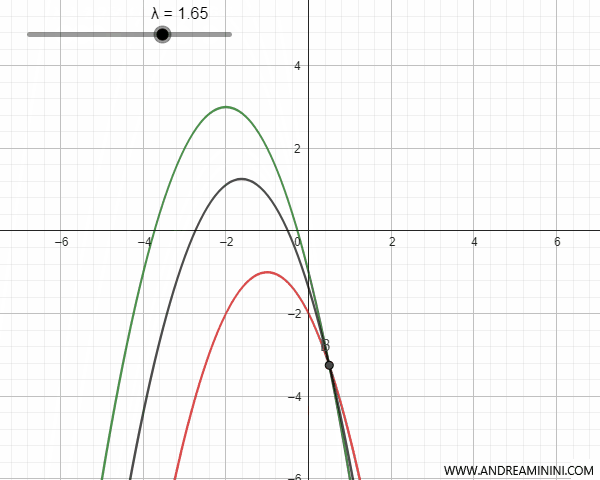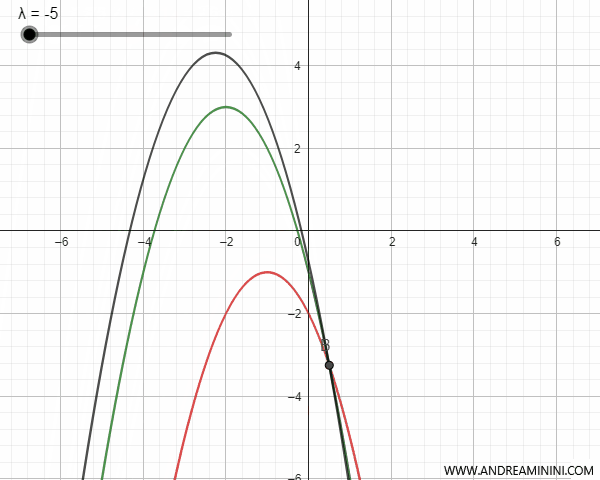
- Le parabole esterne
Le parabole esterne non hanno alcun punto in comune. Quindi, non ci sono punti base del fascio. In un particolare valore del parametro λ la parabola generata può degenerare in una retta situata tra le due parabole.
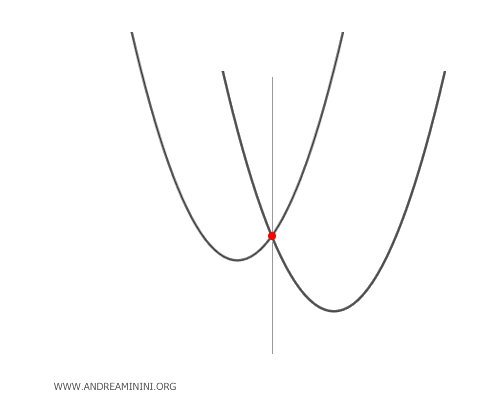
- Le parabole congruenti
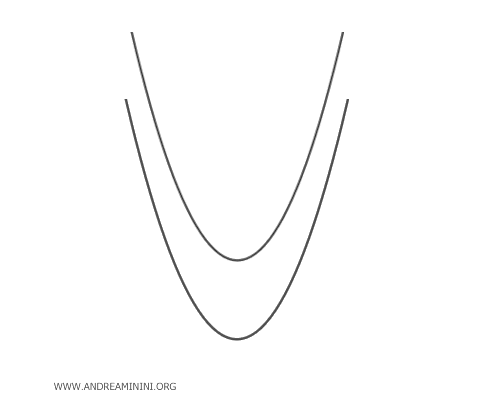
Le parabole congruenti non hanno alcun punto in comune se hanno lo stesso asse di simmetria. E non degenerano in una retta.
Viceversa, se le parabole generatrici sono conguenti e si trovano su assi di simmetria paralleli e non coincidenti, allora si intersecano in un punto base. In quest'ultimo caso, per alcuni valori λ la parabola generata può degenerare in una retta parallela all'asse di simmetria che passa per il punto base.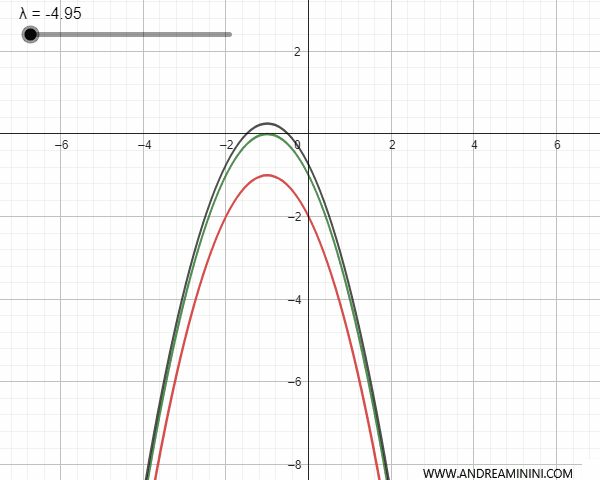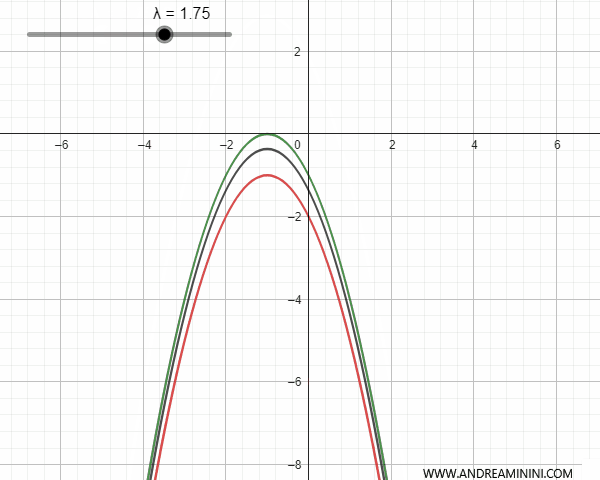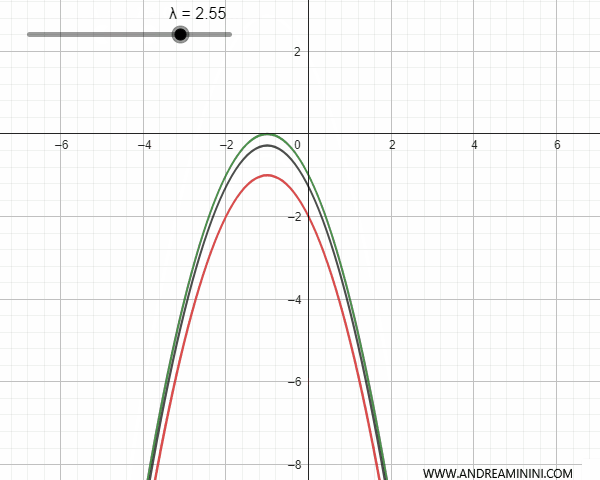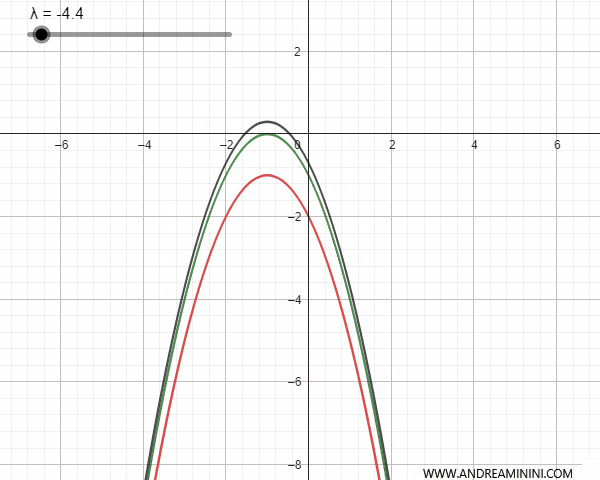
Come trovare le equazioni delle parabole generatrici del fascio
Per trovare le equazioni delle parabole generatrici del fascio, raccolgo i termini rispetto al parametro \(\lambda\)
La prima parabola generatrice si ottiene ponendo \(\lambda = 0 \)
La seconda parabola generatrice si ottiene ponendo a zero l'espressione moltiplicata per \(\lambda \)
Esempio
Considero l'equazione di questo fascio di parabole
$$ (\lambda - 1) x^2 + (3 - 5\lambda) x + (1 + \lambda) y - 2 + 4\lambda = 0 $$
Raccolgo i termini rispetto al parametro \(\lambda\)
$$ (\lambda - 1) x^2 - 5\lambda x + 3x + \lambda y + y + 4\lambda - 2 = 0 $$
$$ (\lambda x^2 - x^2) - 5\lambda x + 3x + \lambda y + y + 4\lambda - 2 = 0 $$
$$ \lambda (x^2 - 5x + y + 4) - x^2 + 3x + y - 2 = 0 $$
La prima generatrice del fascio la trovo ponendo \(\lambda = 0\):
$$ 0 \cdot (x^2 - 5x + y + 4) - x^2 + 3x + y - 2 = 0 $$
$$ -x^2 + 3x + y - 2 = 0 $$
Quindi, la prima generatrice è $ y = x^2 - 3x + 2 $
La seconda generatrice la ottengo ponendo a zero il termine moltiplicato per \(\lambda\):
$$ x^2 - 5x + y + 4 = 0 $$
Quindi, la seconda generatrice è $ y = -x^2 + 5x - 4 $
Ho così trovato entrambe le parabole generatrici del fascio.
Come trovare i punti base del fascio di parabole
Per trovare gli eventuali punti base del fascio di parabole devo risolvere il sistema delle equazioni delle due generatrici.
- Se il sistema ammette due soluzioni, ci sono due punti base e le generatrici sono secanti
- Se il sistema ammette una soluzione, c'è un solo punto base e le generatrici sono tangenti oppure congruenti con diverso asse di simmetria. Quindi, è necessario anche verificare se la condizione di tangenza è soddisfatta o no.
- Se il sistema non ha soluzioni, non ci sono punti base. In questo caso le parabole potrebbero essere esterne oppure congruenti con lo stesso asse di simmetria.
Esempio
Le equazioni delle due generatrici del fascio di parabole sono:
$$ y = x^2 - 3x + 2 $$
$$ y = -x^2 + 5x - 4 $$
Risolvo questo sistema di equazioni per trovare i punti di intersezione.
$$ \begin{cases} y = x^2 - 3x + 2 \\ \\ y = -x^2 + 5x - 4 \end{cases} $$
In questo caso posso porre \( y = x^2 - 3x + 2 \) uguale a \( y = -x^2 + 5x - 4 \) perché sono entrambe uguali a $ y $:
$$ x^2 - 3x + 2 = -x^2 + 5x - 4 $$
Porto tutti i termini sullo stesso lato dell'equazione:
$$ x^2 + x^2 - 3x - 5x + 2 + 4 = 0 $$
$$ 2x^2 - 8x + 6 = 0 $$
Divido tutto per 2 per semplificare:
$$ x^2 - 4x + 3 = 0 $$
Questa è un'equazione quadratica che posso risolvere usando la formula quadratica:
$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
Dove \( a = 1 \), \( b = -4 \), e \( c = 3 \):
$$ x = \frac{4 \pm \sqrt{16 - 12}}{2} $$
$$ x = \frac{4 \pm \sqrt{4}}{2} $$
$$[ x = \frac{4 \pm 2}{2} $$
Quindi, le soluzioni sono:
$$ x = \frac{4 + 2}{2} = 3 $$
$$ x = \frac{4 - 2}{2} = 1 $$
Ora calcolo i valori di \( y \) per i valori di \( x \) trovati:
- Per \( x = 1 \) allora \( y = (1)^2 - 3(1) + 2 = 1 - 3 + 2 = 0 \)
- Per \( x = 3 \) allora \( y = (3)^2 - 3(3) + 2 = 9 - 9 + 2 = 2 \)
Quindi, i punti base del fascio sono \( (1, 0) \) e \( (3, 2) \).
Essendo due punti base non coincidenti, le parabole si intersecano in due punti distinti, quindi le parabole sono secanti.
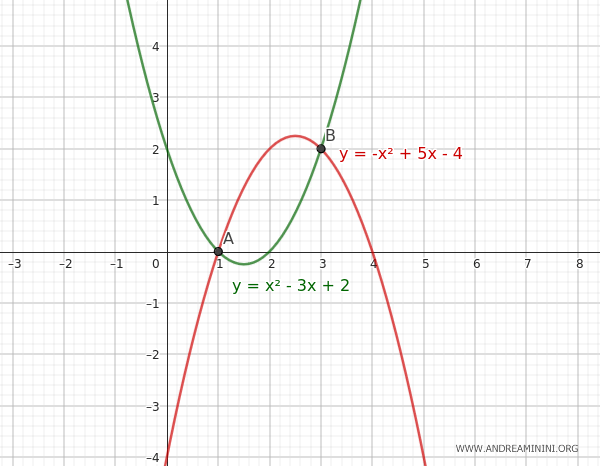
E così via.
