Come determinare l'equazione della parabola dal vertice e la direttrice
Per determinare l'equazione di una parabola parallela all'asse y quando sono note le coordinate del vertice $ V(h;k) $ e l'equazione della retta direttrice $ y_d $, basta utilizzare l'equazione della parabola in forma standard. $$ (x - h)^2 = 4p(y - k) $$ Dove $ p =| k-y_d| $ è la distanza tra il vertice e la retta direttrice.
In una parabola con l'asse di simmetria parallelo all'asse y la direttrice è orizzontale, perché è sempre perpendicolare all'asse di simmetria.
Il fuoco si trova verticalmente opposto al vertice rispetto alla direttrice. Quindi, la distanza tra il vertice $ V(h,k) $ e la direttrice è \(|k - y_d|\) è uguale alla distanza tra il vertice e il fuoco F.
Se la parabola è aperta verso l'alto o verso il basso, l'equazione è della forma:
$$ (x - h)^2 = 4p(y - k) $$
Dove il segno di \(p\) dipende dalla posizione del vertice rispetto alla direttrice:
- Se \(k > y_d\), la parabola è aperta verso l'alto, quindi \(p\) è positivo.
- Se \(k < y_d\), la parabola è aperta verso il basso, quindi \(p\) è negativo.
Nota. Questi passaggi possono essere adattati per altre posizioni del vertice e della direttrice. Se la direttrice è verticale, l'equazione della parabola avrà la forma \((y - k)^2 = 4p(x - h)\).
Un esempio pratico
Supponiamo di avere il vertice \( V (3, 2) \) e la direttrice \( y = -1 \).
La distanza tra l'ordinata del vertice k=2 e la retta direttrice y=-1 è uguale a 3
$$ p = |2 - (-1)| = 3 $$
Una volta individuata la distanza devo capire se la parabola è aperta verso l'alto o verso il basso per stabilire il segno di $ p $.
In questo caso $ k>y $ poichè $ 2>-1 $, quindi la parabola è aperta verso l'alto e il segno del parametro $ p $ è positivo.
$$ p = 3 $$
A questo punto devo solo sostituire i dati che già conosco nell'equazione della parabola in forma standarda.
$$ (x - h)^2 = 4p(y - k) $$
Sapendo che $ p = 3 $ e le coordinate del vertice \( V (3, 2) \) sono $ h = 3 $ e $ k = 2 $
$$ (x - 3)^2 = 4 \cdot 3 \cdot (y - 2) $$
$$ x^2-6x+9 = 12y - 24 $$
$$ 12 y = x^2-6x+9 + 24 $$
$$ y = \frac{x^2}{12}- \frac{6x}{12}+\frac{33}{12} $$
Quindi, l'equazione della parabola con vertice \((3, 2)\) e direttrice \(y = -1\) è:
$$ y = \frac{x^2}{12}- \frac{x}{2}+\frac{33}{12} $$
Sapendo che il fuoco si trova in direzione opposta alla retta direttrice $ y_d $ alla stessa distanza $ p=3 $ dal vertice $ V(h,k)=(3,2) $, deduco che il fuoco si trovi alle coordinate $ F(h,k+p) = (3,5) $ poiché $ h=3 $ e $ k=2 $
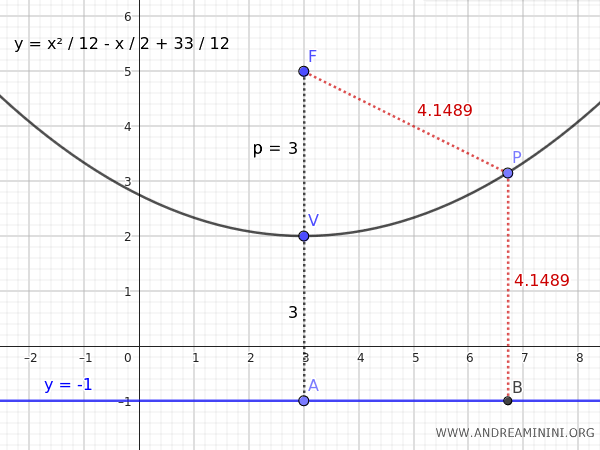
Se prendo un punto $ P $ qualsiasi della parabola, questo si trova alla stessa distanza $ PF $ dal fuoco $ F(3;5) $ e alla stessa distanza $ PB $ dalla direttrice $ y_d=-1 $.
$$ \overline{PF} = \overline{PB} $$
E così via.
