Come scrivere l'equazione della parabola conoscendo un punto, l'asse e la direttrice

Per determinare l'equazione di una parabola dati un punto \( P(x_0, y_0) \), l'asse della parabola ( $ x=h $ o $ y=k ) $  e la direttrice, posso seguire il seguente procedimento. 

• In una parabola con asse verticale $ x_A=h $ la direttrice è una retta orizzontale di equazione \( y_D = k - p \).
  
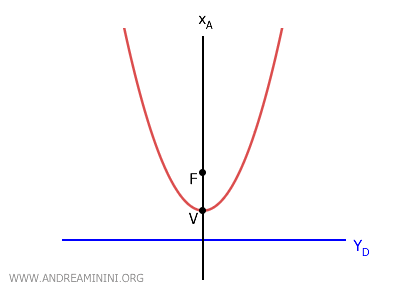
• In una parabola con asse orizzontale $ y_A=k $ la direttrice è una retta verticale di equazione \( x_D = h - p \).
  

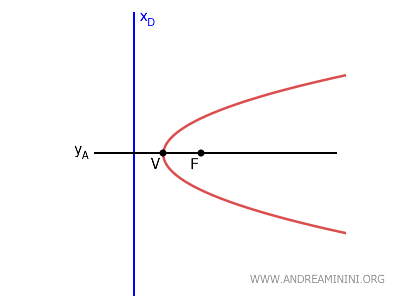
Dove $ (h, k) $ è il vertice della parabola mentre $ p $ è la distanza tra il fuoco e il vertice.

L'equazione dell'asse mi permette di stabilire se la parabola è verticale o orizzontale e, quindi, l'equazione della parabola

• Se l'asse della parabola è verticale $ x=h $, l'equazione della parabola sarà della forma $$ y = ax^2 + bx + c $$ e nella forma standard $$ (x - h)^2 = 4p(y - k) $$
• Se l'asse della parabola è orizzontale $ y=k $, l'equazione della parabola sarà della forma $$ x = ay^2 + by + c $$ e nella forma standard $$ (y - k)^2 = 4p(x - h) $$

La conoscenza delle coordinate del punto e l'equazione della direttrice mi permette di capire l'apertura della parabola.

• Se la parabola è verticale e la direttrice si trova sotto l'ordinata del punto P, allora l'apertura della parabola è verso l'alto. Viceversa, se la direttrice si trova sopra rispetto il punto l'apertura è verso il basso.
  
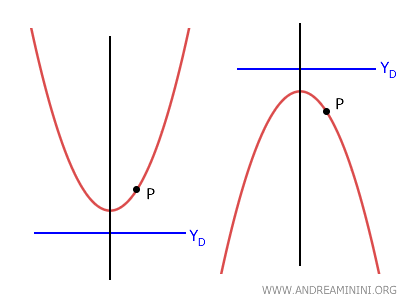
• Se la parabola è orizzontale e la direttrice si trova a sinistra dell'ascissa del punto P, allora l'apertura della parabola è verso destra. Viceversa, se la direttrice si trova a destra rispetto il punto l'apertura è verso sinistra.
  

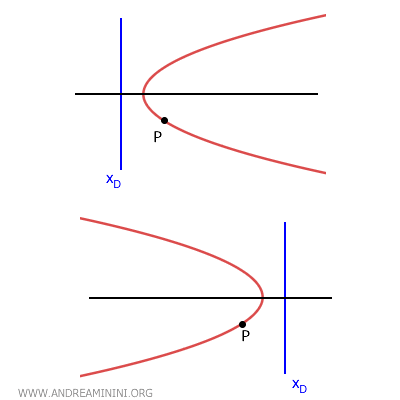
Infine, utilizzo le coordinate del punto \( P(x_0, y_0) \) per determinare i parametri mancanti.

• Per una parabola con asse verticale, sostituisco \( x_0 \) e \( y_0 \) nell'equazione \( (x_0 - h)^2 = 4p(y_0 - k) \) e risolvo per \( h \), \( k \), e \( p \).
• Per una parabola con asse orizzontale, sostituisco \( x_0 \) e \( y_0 \) nell'equazione \( (y_0 - k)^2 = 4p(x_0 - h) \) e risolvere per \( h \), \( k \), e \( p \).

Un esempio pratico

Considero il punto \( P(5, 6) \), la direttrice \( y_D = 2 \) e l'asse verticale \( x_A = 1 \)

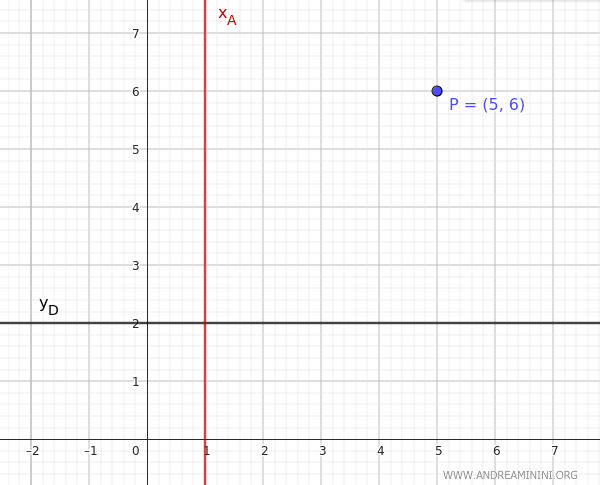
In questo caso la direttrice $ y_D=2 $ è orizzontale e l'asse di simmetria $ x_A = 1 $ è verticale, quindi la parabola è verticale.

L'ordinata del punto $ P(5,6) $ noto è $ y_0=6 $ ed è superiore alla direttrice $ y_D=1 $, quindi deduco che la parabola è aperta verso l'alto.

Sapendo che la parabola è verticale, posso iniziare a scrivere l'equazione standard della parabola.

$$ (x - h)^2 = 4p(y - k) $$

Non conosco le coordinate del vertice $ V(h,k) $ né quelle del fuoco $ F(x_F,y_F) $

Tuttavia, sapendo che il vertice e il fuoco sono due punti dell'asse di simmetria $ x_A=1 $, deduco abbiano la stessa ascissa, ovvero $ h =1 $ e $ x_F = 1 $

$$ V(h,k) = (1,k) $$

$$ F(x_F,y_F) = (1,y_F) $$

Sostituisco $ h = 1 $ nell'equazione della parabola

$$ (x - 1)^2 = 4p(y - k) $$

Il parametro $ p = y_F-k $ misura la distanza tra il fuoco $ F(x_F,y_F) $ e il vertice $ V(h,k) $

$$ p = y_F - k $$

In questo caso però non conosco le ordinate del fuoco $ F (1,y_F) $, quindi non mi è utile.

Tuttavia, sapendo che la distanza $ p = y_F - k $ tra il fuoco e il vertice  è uguale alla distanza $ p = k - y_D $ tra il vertice $ V(h,k) = (1,k) $  e la direttrice $ y_D=2 $ che già conosco,  posso ottenere la distanza $ p $ anche in quest'altro modo:

$$ p = k - y_D $$

$$ p = k - 2 $$

Quindi, sostituisco $ p = k-2 $ nell'equazione della parabola

$$ (x - 1)^2 = 4p(y - k) $$

$$ (x - 1)^2 = 4(k-2)(y - k) $$

Così facendo ho ridotto il numero delle incognite dell'equazione.

Infine, poiché il punto \( P(5, 6) \) appartiene alla parabola e soddisfa l'equazione, sostituisco le coordinate $ x=5 $ e $ p=6 $ nell'equazione della parabola

$$ (5 - 1)^2 = 4(k-2)(6 - k) $$

Questo mi consente di risolvere l'equazione per trovare $ k $, ovvero l'ordinata del vertice $ V(h,k)=(1,k) $ che ancora non conosco

$$ 4^2 = 4(k-2)(6 - k) $$

$$ 16 = 4(k-2)(6 - k) $$

Semplifico dividendo entrambi i lati dell'equazione per 4

$$ 4 = (k-2)(6 - k) $$

$$ 4 = 6k-k^2-12+2k $$

$$ -k^2+8k-12-4=0 $$

$$ -k^2+8k-16=0 $$

Il discriminante dell'equazione di secondo grado è

$$ \Delta = b^2-4ac = 8^2-4 \cdot (-1) \cdot (-16) = 64 -64 = 9 $$

Quindi, l'equazione di 2° grado ha un'unica soluzione

$$ k = \frac{-b \pm \sqrt{\Delta}}{2a} $$

$$ k = \frac{-8 \pm \sqrt{0}}{2 \cdot (-1)} $$

$$ k =\frac{ -8}{-2} $$

$$ k = 4 $$

Pertanto, il vertice della parabola si trova alle coordinate $ V(h,k)=(1,4) $

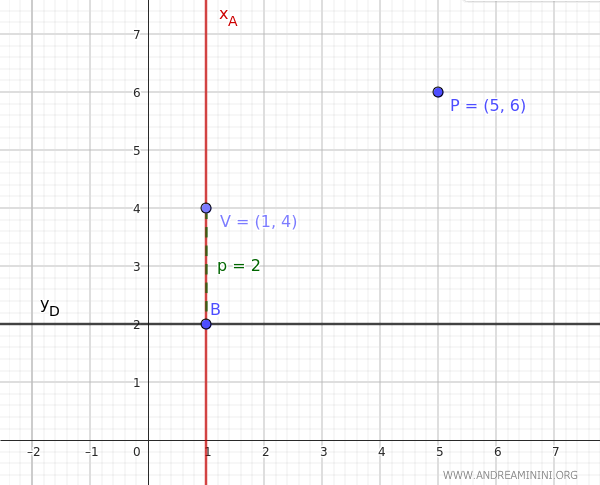
Una volta noto k posso calcolare la distanza tra il vertice e la direttrice

$$ p = k - y_D = 4 - 2 = 2 $$

A questo punto ho tutte le informazioni necessarie ( h=1, k=4, p=2 ) per completare l'equazione in forma standard della parabola.

$$ (x - h)^2 = 4p(y - k) $$

$$ (x - 1)^2 = 4 \cdot 2 \cdot (y - 4) $$

$$ x^2 -2x +1 = 8y - 32$$

$$ x^2 -2x +1 + 32 - 8y = 0 $$

$$ x^2-2x-8y+33= 0 $$

Ecco la rappresentazione grafica.

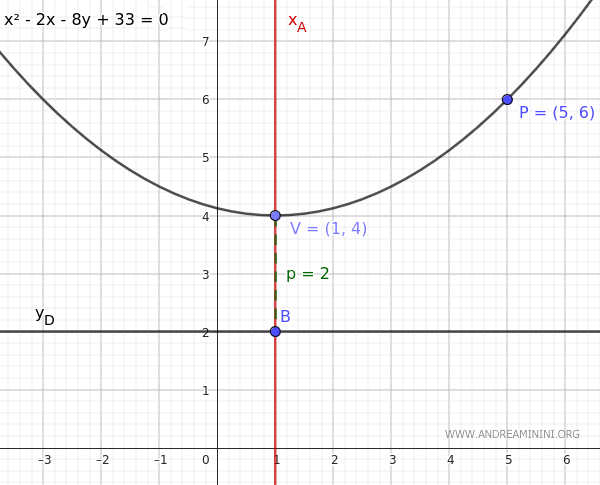
E così via.