L'equazione della parabola parallela all'asse y in forma standard
L'equazione in forma standard di una parabola con vertice \((h, k)\) e asse di simmetria parallelo all'asse \(y\) è $$ (x - h)^2 = 4p(y - k) $$ Dove $ p $ è la distanza dal fuoco \((x_F, y_F) \) al vertice \((h, k)\). $$ p = y_F - k $$
Questa equazione deriva dalla definizione geometrica di una parabola come il luogo dei punti equidistanti da un punto fisso (fuoco) e una linea fissa (direttrice).
La distanza $ p $ determina l'apertura della parabola
- Se $ p>0 $ la parabola è aperta verso l'alto
- Se $ p<0 $ la parabola è aperta verso il basso
E' particolarmente utile perché rende immediatamente visibile la posizione del vertice e la distanza dal vertice al fuoco, semplificando l'analisi della parabola.
Un esempio pratico
Il fuoco di una parabola si trova alle coordinate $ F(3;2) $ mentre il vertice si trova alle coordinate $ V(3;1) $
Si tratta di una parabola con l'asse di simmetria parallelo all'asse y perché il fuoco e il vertice hanno la stessa componente x=3.
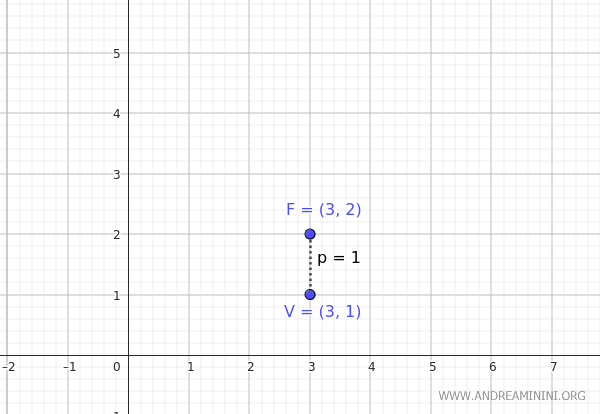
Per determinare l'equazione della parabola utilizzo la formula dell'equazione in forma standard:
$$ (x - h)^2 = 4p(y - k) $$
In questo caso la distanza dal fuoco al vertice è $ p = y_F - k = 2-1=1 $
$$ (x - h)^2 = 4 \cdot 1 (y - k) $$
$$ (x - h)^2 = 4 (y - k) $$
Le coordinate del vertice sono $ h=3 $ e $ k =1 $
$$ (x - 3)^2 = 4 (y - 1) $$
$$ x^2-6x+9 = 4y - 4 $$
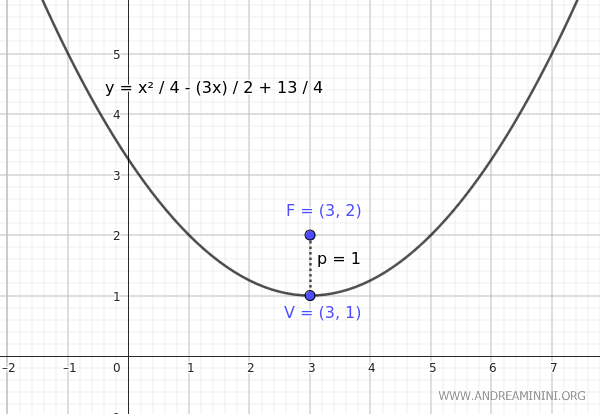
Quindi l'equazione della parabola è
$$ y = \frac{ x^2}{4}- \frac{3x}{2}+ \frac{13}{4} $$
In questo modo ho ottenuto l'equazione della parabola a partire dal fuoco e dal vertice.
Verifica
Nell'equazione della parabola la distanza tra il fuoco F e punto qualsiasi P della parabola è sempre uguale alla distanza tra lo stesso punto P e la retta direttrice della parabola.
Una volta nota l'equazione di secondo grado della parabola, posso calcolare l'equazione della retta direttrice
$$ y= - \frac{1+Δ}{4a} $$
Dove $ \Delta = b^2-4ac $ è il discriminante dell'equazione della parabola $ y = \frac{ x^2}{4}- \frac{3x}{2}+ \frac{13}{4} $
I coefficienti dell'equazione sono $ a = \frac{1}{4} $, $ b= - \frac{3}{2} $ , $ c= \frac{13}{4} $
$$ \Delta = b^2-4ac $$
$$ \Delta = (- \frac{3}{2})^2-4 \cdot \frac{1}{4} \cdot \frac{13}{4} $$
$$ \Delta = \frac{9}{4} - \frac{13}{4} $$
$$ \Delta = \frac{9-13}{4} $$
$$ \Delta = \frac{-4}{4} $$
$$ \Delta = -1 $$
Quindi, l'equazione della retta direttrice della parabola è
$$ y= - \frac{1+Δ}{4a} $$
$$ y= - \frac{1-1}{4 \cdot \frac{1}{4}} $$
$$ y= 0 $$
In questo caso la retta direttrice coincide con l'asse delle ascisse.
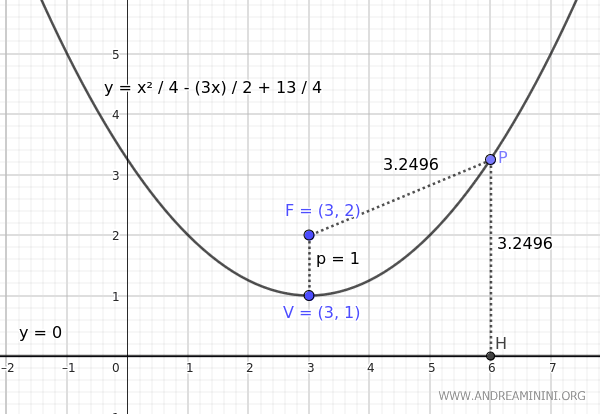
Preso un punto P qualsiasi della parabola, la distanza tra il punto e il fuoco è uguale a quella tra il punto e la retta direttrice (PF≅PH).
Pertanto, l'equazione della parabola è corretta.
Nota. In questo esempio ho svolto tutti i calcoli per ottenere la retta direttrice. L'ho fatto solo per completezza ma non è necessario farlo. Si può giungere molto più facilmente allo stesso risultato considerando che la retta direttrice è perpendicolare (90°) all'asse di simmetria della parabola (che in questo caso è parallelo all'asse y) e si trova alla stessa distanza dal vertice V rispetto alla distanza tra il vertice V e il fuoco F ma in direzione opposta. In questo caso, la distanza tra il vertice è il fuoco è VF=1 e il vertice V si trova alle coordinate (3,1), quindi si può dedurre che la retta direttrice passa per il punto (3,0) ed è y=0 senza fare alcun calcolo.
La dimostrazione
Una parabola è il luogo dei punti tali che la distanza da un punto fisso, detto fuoco \((h, k + p)\), è uguale alla distanza da una linea retta fissa, detta direttrice \(y = k - p\).
La distanza da un punto della parabola \( P(x, y)\) al fuoco \((h, k + p)\) è
$$ \sqrt{(x - h)^2 + (y - (k + p))^2} $$
La distanza dallo stesso punto \(P(x, y)\) alla direttrice \(y = k - p\) è
$$ |y - (k - p)| $$
Secondo la definizione di parabola, queste due distanze sono uguali:
$$ \sqrt{(x - h)^2 + (y - (k + p))^2} = |y - (k - p)| $$
Poiché la distanza è sempre positiva, posso riscrivere la distanza dalla direttrice eliminando il valore assoluto
$$ \sqrt{(x - h)^2 + (y - (k + p))^2} = y - (k - p) $$
Elevo al quadrato entrambi i membri:
$$ \left( \sqrt{(x - h)^2 + (y - (k + p))^2} \right)^2 = \left( y - (k - p) \right)^2 $$
$$ (x - h)^2 + (y - (k + p))^2 = (y - (k - p))^2 $$
$$ (x - h)^2 + (y - k - p)^2 = (y - k + p)^2 $$
A questo punto espando i quadrati:
$$ (x - h)^2 + (y - k - p)^2 = (y - k + p)^2 $$
$$ (x - h)^2 + (y - k)^2 - 2p(y - k) + p^2 = (y - k)^2 + 2p(y - k) + p^2 $$
Cancello i termini comuni da entrambi i lati dell'equazione
$$ (x - h)^2 - 2p(y - k) = 2p(y - k) $$
$$ (x - h)^2 = 2p(y - k) + 2p(y - k) $$
$$ (x - h)^2 = 4p(y - k) $$
Quindi, l'equazione standard della parabola con vertice \((h, k)\) e asse di simmetria parallelo all'asse \(y\) è:
$$ (x - h)^2 = 4p(y - k) $$
Dove \(p\) è la distanza dal vertice al fuoco e \(4p\) è una costante che determina l'apertura della parabola.
Più grande è \(p\), più larga è la parabola; più piccolo è \(p\), più stretta è la parabola.
In conclusione, la forma standard \((x - h)^2 = 4p(y - k)\) deriva direttamente dalla definizione geometrica della parabola e dalla relazione tra il fuoco e la direttrice.
E così via.
