Come ottenere l'equazione di una parabola dati due punti e l'asse

Se conosco due punti distinti \((x_1, y_1)\) e \((x_2, y_2)\) e l'equazione dell'asse di simmetria \( x = h \) della parabola, posso determinare l'equazione della parabola, seguendo questi passaggi

1. Una parabola parallela all'asse y ha la forma $$ y = a(x - h)^2 + k $$ dove \( (h, k) \) è il vertice della parabola.
2. Sostituisco i due punti noti nell'equazione della parabola: $$ y_1 = a(x_1 - h)^2 + k $$ $$ y_2 = a(x_2 - h)^2 + k $$ dove $ (h,k) $ sono le coordinate del vertice della parabola.
3. Queste sono due equazioni con due incognite (\( a \) e \( k \)). Quindi, posso risolvere il sistema per trovare \( a \) e \( k \) e completare l'equazione della parabola.

Metodo alternativo. In alternativa, se i due punti \((x_1, y_1)\) e \((x_2, y_2)\) non sono simmetrici rispetto all'asse $ x=h $, potrei ottenere le coordinate di un terzo punto  \((x_3, y_3)\) simmetrico rispetto a uno dei due punti precedenti e determinare l'equazione della parabola noti tre punti.

Un esempio pratico

Dati due punti \((2, 3)\) e \((3,5)\) e l'asse di simmetria \( x = 1 \) della parabola, devo ricavare l'equazione della parabola.

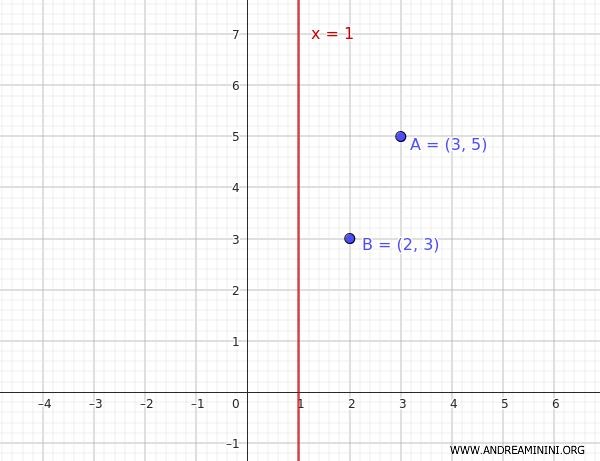
La forma generale di una parabola parallela all'asse y è:

$$ y = a(x - h)^2 + k $$

Dove $ (h,k) $ è il vertice V della parabola.

In questo caso l'asse di simmetria della parabola è $ x=1 $, quindi $ h = 1 $ poiché il vertice $ V (h,k)=(1,k) $ è un punto dell'asse.

$$ y = a(x - 1)^2 + k $$

Scrivo un sistema di equazioni sostituendo le coordinate dei due punti noti \((x_1,y_1)=(2, 3)\) e \((x_2,y_2)=(3, 5)\) nell'equazione generale della parabola

$$ \begin{cases} y_1 = a(x_1 - 1)^2 + k \\ \\ y_1 = a(x_1 - 1)^2 + k \end{cases} $$

$$ \begin{cases} 3 = a(2 - 1)^2 + k \\ \\ 5 = a(3 - 1)^2 + k \end{cases} $$

$$ \begin{cases} 3 = a(1)^2 + k \\ \\ 5 = a(2)^2 + k \end{cases} $$

$$ \begin{cases} 3 = a + k \\ \\ 5 = 4a + k \end{cases} $$

Si tratta di un sistema a due equazioni e due incognite.

Provo a risolverlo con il metodo della sostituzione per individuare i valori delle incognite $ a $ e $ k $

$$ \begin{cases} k = 3 - a  \\ \\ 5 = 4a + k \end{cases} $$

$$ \begin{cases} k = 3 - a  \\ \\ 5 = 4a + (3-a) \end{cases} $$

$$ \begin{cases} k = 3 - a  \\ \\ 5 = 3a + 3 \end{cases} $$

$$ \begin{cases} k = 3 - a  \\ \\ 3a = 2 \end{cases} $$

$$ \begin{cases} k = 3 - a  \\ \\ a = \frac{2}{3} \end{cases} $$

$$ \begin{cases} k = 3 -  \frac{2}{3}  \\ \\ a = \frac{2}{3} \end{cases} $$

$$ \begin{cases} k =  \frac{9-2}{3}  \\ \\ a = \frac{2}{3} \end{cases} $$

$$ \begin{cases} k =  \frac{7}{3}  \\ \\ a = \frac{2}{3} \end{cases} $$

Una volta ottenuto $ k $ conosco le coordinate del vertice $ (h,k)=(1, \frac{7}{3} $

Inoltre, poiché conosco anche $ a = \frac{2}{3} $ e $ h =1 $ posso scrivere l'equazione generale della parabola.

$$ y = a(x - h)^2 + k $$

$$ y = \frac{2}{3} \cdot (x - 1)^2 + \frac{7}{3} $$

Ecco la rappresentazione grafica

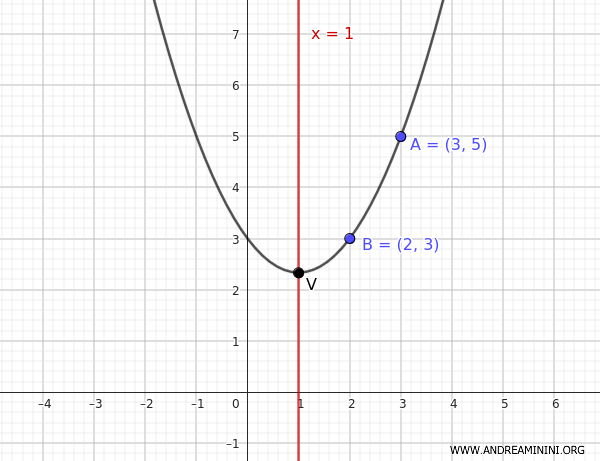
Soluzione alternativa

Conosco le coordinate di due punti \( (2, 3)\) e \((3,5)\) e l'asse di simmetria \( x = 1 \) della parabola.

 

I due punti non sono simmetrici tra loro rispetto all'asse di simmetria $ x=1 $

Scelgo uno dei due punti, ad esempio $ B (2,3) $, e calcolo un terzo punto $ C(0,3) $ simmetrico rispetto all'asse $ x=1 $

Infatti, quando l'asse di simmetria è parallelo alle ordinate secondo la simmetria assiale un punto è simmetrico a un altro se

$$ \begin{cases} x' = 2h - x \\ \\ y' = y' \end{cases} $$

In questo caso, l'asse di simmetria è $ h=1 $ e  le coordinate del punto B sono $ x=2 $ e $ y=3 $

$$ \begin{cases} x' = 2 \cdot 1 - 2 \\ \\ y' = 3 \end{cases} $$

$$ \begin{cases} x' = 0 \\ \\ y' = 3 \end{cases} $$

Quindi, le coordinate del terzo punto sono $ C(0,3) $

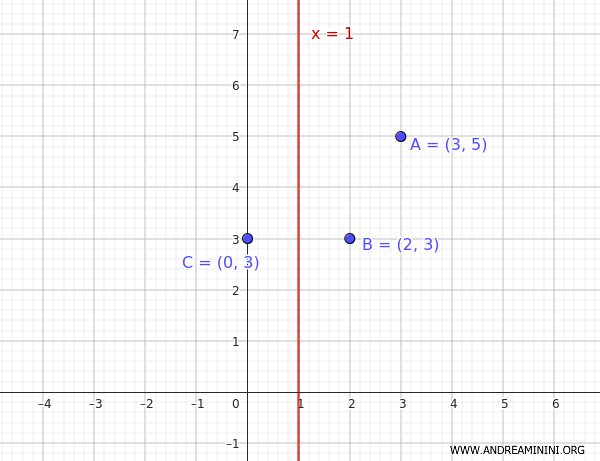
A questo punto, note le coordinate di tre punti $ A(3,5) $, $ B(2,3) $ e $ C(0,3) $ posso costruire un sistema di tre equazioni.

$$ \begin{cases} ax_1^2 + bx_1 + c = y_1 \\ \\ ax_2^2 + bx_2 + c = y_2 \\ \\ ax_3^2 + bx_3 + c = y_3 \\ \end{cases} $$

A ciascuna equazione sostituisco le coordinate di uno dei punti noti.

$$ \begin{cases} a \cdot 3^2 + b \cdot 3 + c = 5 \\ \\ a \cdot 2^2 + b \cdot 2 + c = 3 \\ \\ a \cdot 0^2 + b \cdot 0 + c = 3 \\ \end{cases} $$

$$ \begin{cases} 9a + 3b + c = 5 \\ \\ 4a + 2b + c = 3 \\ \\ c = 3 \\ \end{cases} $$

Quindi, risolvo il sistema per trovare i coefficienti a, b, c

$$ \begin{cases} 9a + 3b + 3 = 5 \\ \\ 4a + 2b + 3 = 3 \\ \\ c = 3 \\ \end{cases} $$

$$ \begin{cases} 9a + 3b= 2 \\ \\ 4a + 2b = 0 \\ \\ c = 3 \\ \end{cases} $$

$$ \begin{cases} 9a + 3b= 2 \\ \\  b = \frac{-4a}{2} \\ \\ c = 3 \\ \end{cases} $$

$$ \begin{cases} 9a + 3b= 2 \\ \\  b = -2a \\ \\ c = 3 \\ \end{cases} $$

$$ \begin{cases} 9a + 3 \cdot (-2a) = 2 \\ \\  b = -2a \\ \\ c = 3 \\ \end{cases} $$

$$ \begin{cases} 9a - 6a = 2 \\ \\  b = -2a \\ \\ c = 3 \\ \end{cases} $$

$$ \begin{cases} 3a = 2 \\ \\  b = -2a \\ \\ c = 3 \\ \end{cases} $$

$$ \begin{cases} a = \frac{2}{3} \\ \\  b = -2a \\ \\ c = 3 \\ \end{cases} $$

$$ \begin{cases} a = \frac{2}{3} \\ \\  b = -2 \cdot \frac{2}{3} \\ \\ c = 3 \\ \end{cases} $$

$$ \begin{cases} a = \frac{2}{3} \\ \\  b = - \frac{4}{3} \\ \\ c = 3 \\ \end{cases} $$

Ho trovato i coefficienti a, b, c che posso sostituire nell'equazione della parabola

$$ y = ax^2 + bx + c $$

$$ y = \frac{2}{3} x^2 - \frac{4}{3}x + 3 $$

In questo modo ho determinato l'equazione della parabola.

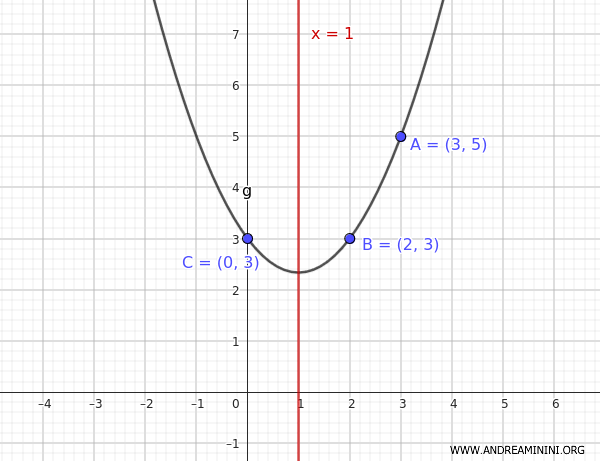
E così via.