Come ottenere l'equazione di una parabola dato il fuoco e il vertice
Per determinare l'equazione di una parabola parallela all'asse y conoscendo le coordinate del vertice \( V(h, k)\) e del fuoco \( F(h, k + p)\), posso seguire questi passaggi:
- Determino la distanza del fuoco dal vertice
La distanza \( p \) tra il vertice e il fuoco è la differenza tra la coordinata y del fuoco ( $ k+p $ ) e la coordinata y del vertice ( $ k $ ) $$ p = (k + p) - k = p $$ - Scrivo l'equazione della parabola
La forma standard dell'equazione di una parabola con il vertice \((h, k)\) e l'asse di simmetria parallelo all'asse y è:
$$ (x - h)^2 = 4p(y - k) $$
Un esempio pratico
Il vertice della parabola è \((h, k) = (2, 3)\) e il fuoco sia \((2, 5)\).
Devo determinare l'equazione della parabola.
Per prima cosa calcolo la distanza tra il fuoco e il vertice
$$ p = 5 - 3 = 2 $$
Poi scrivo l'equazione della parabola in forma standard.
$$ (x - h)^2 = 4p(y - k) $$
Sapendo che p=2, h=2 e k=3.
$$ (x - 2)^2 = 8(y - 3) $$
Quindi, l'equazione della parabola con vertice \((2, 3)\) e fuoco \((2, 5)\) è:
$$ (x - 2)^2 = 8(y - 3) $$
$$ x^2-4x+4 = 8y - 24 $$
$$ 8y = x^2-4x+4+24 $$
$$ y = \frac{x^2}{8} - \frac{4x}{8}+ \frac{28}{8} $$
$$ y = \frac{x^2}{8} - \frac{x}{2}+ \frac{7}{2} $$
Ecco la rappresentazione grafica
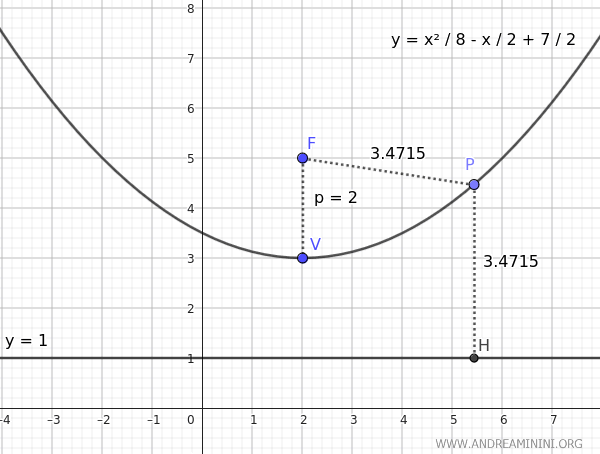
Nota. Sapendo che la retta direttrice è perpendicolare all'asse simmetrico della parabola e si trova alla stessa distanza dal vertice V rispetto al fuoco, deduco senza fare altri calcoli che la retta direttrice sia l'equazione y=1. In questo modo posso subito verificare che la distanza PF tra un punto P qualsiasi e il fuoco F è uguale alla distanza PH tra lo stesso punto e la retta direttrice.
Questo è il processo per generare l'equazione di una parabola conoscendo le coordinate del vertice e del fuoco.
E così via.
