Come determinare l'equazione della parabola dato un punto e la retta direttrice
Per generare l'equazione della parabola conoscendo le coordinate del fuoco \((h, k)\) e l'equazione della retta direttrice \(y = d\) o \(y = x\), posso seguire questi passaggi:
- Se la retta direttrice è orizzontale \(y = d\)
L'equazione della parabola può essere trovata come segue:- La distanza di un punto generico \((x, y)\) dal fuoco è $ \sqrt{(x - h)^2 + (y - k)^2} $
- La distanza di un punto generico \((x, y)\) dalla direttrice è $ |y - d| $
- L'equazione della parabola si ottiene uguagliando le distanze perché ua parabola è il luogo dei punti che sono equidistanti dal fuoco e dalla direttrice. $$ \sqrt{(x - h)^2 + (y - k)^2} = |y - d| $$ Risolvendo l'equazione: $$
(x - h)^2 + (y - k)^2 = (y - d)^2 $$ Espandendo e semplificando si ottiene l'equazione della parabola in forma canonica.
- Se la retta direttrice è verticale \(x = d\)
In questo caso l'equazione della parabola posso trovarla in modo simile:- La distanza di un punto generico \((x, y)\) dal fuoco è $ \sqrt{(x - h)^2 + (y - k)^2} $
- La distanza di un punto generico \((x, y)\) dalla direttrice è $ |x - d| $
- L'equazione della parabola la ottengo uguagliando le distanze, perché per definizione in una parabola la distanza tra un punto e il fuoco è uguale alla distanza tra lo stesso punto e la retta direttrice $$ \sqrt{(x - h)^2 + (y - k)^2} = |x - d| $$ Risolvo l'equazione $$ (x - h)^2 + (y - k)^2 = (x - d)^2 $$ Espandendo e semplificando ottengo l'equazione della parabola in forma canonica.
Un esempio pratico
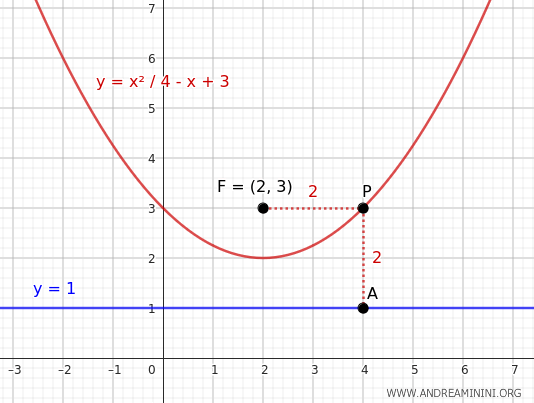
In questo esempio il fuoco è \( F (2, 3) \) e la retta direttrice è \( y = 1 \).
La retta direttrice è orizzontale, quindi l'asse di simmetria della parabola è parallelo all'asse dell'ascisse.
Per definizione, la distanza di un punto \( P(x,y) \) della parabola ha la stessa distanza sia dal fuoco \( F (2, 3) \) che dalla retta direttrice \( y = 1 \).
$$ \sqrt{(x - 2)^2 + (y - 3)^2} = |y - 1| $$
Per la proprietà invariantiva elevo al quadrato entrambi i lati dell'equazione:
$$ \left( \sqrt{(x - 2)^2 + (y - 3)^2} \right)^2 = ( |y - 1| )^2 $$
$$ (x - 2)^2 + (y - 3)^2 = (y - 1)^2 $$
Espando e semplifico
$$ x^2-4x+4 + y^2 - 6y + 9 = y^2 - 2y + 1 $$
$$ x^2-4x + 13-1 = -2y + 6y $$
$$ x^2-4x + 12 = 4y $$
$$ y = \frac{x^2}{4} - \frac{4x}{4} + \frac{12}{4} $$
$$ y = \frac{x^2}{4} - x + 3 $$
Questa è l'equazione della parabola con il fuoco \( (2, 3) \) e la direttrice \( y = 1 \).
In questo modo, posso ottenere l'equazione di una parabola conoscendo le coordinate del fuoco e della retta direttrice.
E così via.
