Retta tangente, secante o esterna a una parabola
Una retta può essere tangente, secante o esterna a una parabola se ha rispettivamente un punto, due punti o nessun punto in comune con la parabola.
Per trovare i punti in comune basta risolvere un'equazione di secondo grado.
$$ ax^2+x \cdot (b-m)+c-q=0 $$
Dove $ a $, $ b $ e $ c $ sono i coefficienti dell'equazione della parabola $ y= ax^2+bx+c $ mentre $ m $ e $ q $ sono rispettivamente il coefficiente angolare e il termine noto dell'equazione della retta $ y = mx+q $.
L'equazione ha una, due o nessuna soluzione se il discriminante $ \Delta = b^2+4ac $ è uguale a zero, minore di zero o maggiore di zero.
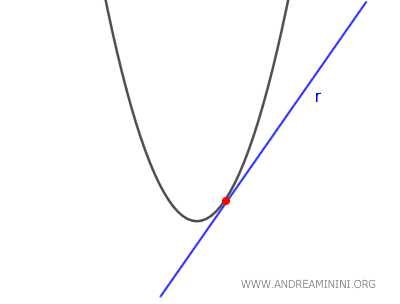
- Se $ \Delta = 0 $ la retta è tangente alla parabola, perché l'equazione ammette una soluzione reale, quindi la retta e la parabola hanno un solo punto in comune.
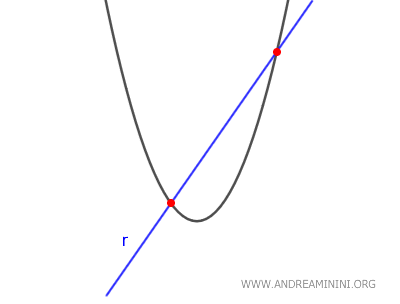
- Se $ \Delta > 0 $ la retta è secante alla parabola, perché l'equazione ammette due soluzioni reali e distinte, quindi ci sono due punti di intersezione tra la retta e la parabola.
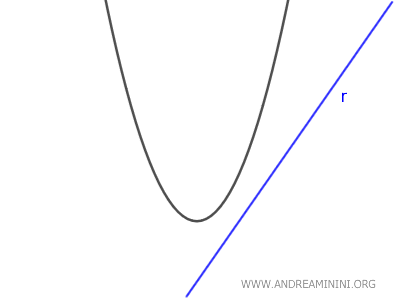
- Se $ \Delta <0 $ la retta è esterna alla parabola, perché l'equazione non ha soluzioni reali. Quindi, non ci sono punti in comune tra la retta e la parabola.
Nota. Questo criterio si applica solo se la retta non è parallela all'asse delle ordinate, perché quando la retta è verticale non può essere rappresentata dall'equazione esplicita $ y = mx+q $.
Un esempio pratico
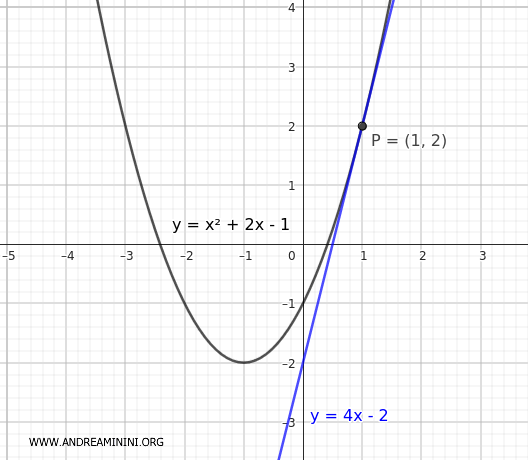
Considero una parabola con la sequente equazione
$$ y = x^2+2x-1 $$
e una retta
$$ y = 4x-2 $$
Devo capire se la retta è tangente, secante o esterna alla parabola.
Per trovare gli eventuali punti in comune, eguaglio le due equazioni
$$ x^2+2x-1 = 4x-2 $$
$$ x^2+2x-1-4x+2 = 0 $$
$$ x^2-2x+1 = 0 $$
Calcolo il discriminante di questa equazione di secondo grado
$$ \Delta=\sqrt{b^2-4ac} $$
In questo caso i coefficienti sono a=1, b=-2, c=1
$$ \Delta=\sqrt{(-2)^2-4 \cdot 1 \cdot 1} $$
$$ \Delta=\sqrt{4-4} $$
$$ \Delta=0 $$
Il discriminante è nullo, quindi l'equazione ha una sola soluzione reale.
Questo vuol dire che la retta è tangente alla parabola.
Per trovare il punto di tangenza calcola la soluzione dell'equazione di secondo grado
$$ x = \frac{-b \pm \sqrt{\Delta}}{2a} $$
$$ x = \frac{-(-2) \pm \sqrt{0}}{2 \cdot 1} $$
$$ x = \frac{2}{2} $$
$$ x = 1 $$
Una volta nota la componente x del punto di tangenza, calcolo anche la componente y delle coordinate, sostituendo x=1 nell'equazione della retta.
$$ y = 4x-2 $$
$$ y = 4 \cdot 1-2 $$
$$ y = 2 $$
Quindi, il punto di tangenza P si trova alle coordinate $ (x;y)=(1;2) $
La dimostrazione
L'equazione di una parabola è
$$ y=ax^2+bx+c $$
L'equazione di una retta non parallela all'asse y è
$$ y = mx+q $$
Per trovare i punti di intersezione tra la retta e la parabole, devo cercare quali valori della x soddisfano entrambe equazioni
$$ y = y $$
$$ ax^2+bx+c = mx+q $$
$$ ax^2+bx-mx+c-q=0 $$
$$ ax^2+x \cdot (b-m)+c-q=0 $$
Per trovare le soluzioni dell'equazione di secondo grado utilizzo la formula
$$ x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$
Un'equazione di secondo grado può avere una, due o nessuna soluzione a seconda se il discriminante $ \Delta = b^2-4ac $ è rispettivamente uguale a zero, maggiore di zero o minore di zero.
- Se $ \Delta = 0 $ l'equazione ha una soluzione reale, quindi la retta e la parabola hanno un solo punto in comune, ovvero la retta è tangente alla parabola.
- Se $ \Delta > 0 $ l'equazione ha due soluzioni reali e distinte, quindi la retta e la parabola hanno due punti in comune, ovvero due punti di intersezione. Quindi, la retta è secante alla parabola.
- Se $ \Delta < 0 $ l'equazione non ha nessuna soluzione reale, quindi la retta e la parabola non hanno alcun punto in comune, ovvero la retta è esterna alla parabola.
E così via
