Come determinare l'equazione della parabola conoscendo tre punti

Per determinare l'equazione di una parabola conoscendo tre punti \( A(x_1, y_1)\), \( B(x_2, y_2)\), \( C(x_3, y_3)\), posso utilizzare il metodo delle equazioni simultanee. $$
\begin{cases}
ax_1^2 + bx_1 + c = y_1 \\ \\ ax_2^2 + bx_2 + c = y_2 \\ \\ ax_3^2 + bx_3 + c = y_3 \\ \end{cases} $$

L'equazione di una parabola nella forma standard è:

\[ y = ax^2 + bx + c \]

Quindi, se conosco le coordinate di tre punti distinti \( A(x_1, y_1)\), \( B(x_2, y_2)\), \( C(x_3, y_3)\) della parabola, posso sostituire ciascun punto nell'equazione della parabola e ottenere un sistema di tre equazioni lineari:

$$ y_1 = ax_1^2 + bx_1 + c $$

$$ y_2 = ax_2^2 + bx_2 + c $$

$$  y_3 = ax_3^2 + bx_3 + c $$

Queste equazioni posso scriverle in un sistema lineare:

$$
\begin{cases}
ax_1^2 + bx_1 + c = y_1 \\ \\ ax_2^2 + bx_2 + c = y_2 \\ \\ ax_3^2 + bx_3 + c = y_3 \\ \end{cases} $$

Risolvendo questo sistema posso trovare i valori dei coefficienti "a", "b", "c" dell'equazione della parabola $ y = ax^2+bx+c $ che passa per i tre punti.

Un esempio pratico

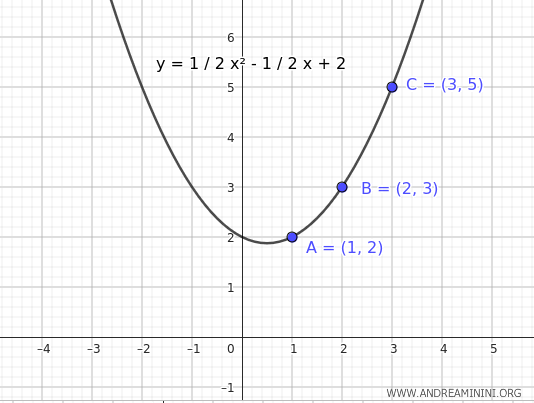
Considero tre punti distinti del piano \( A(1, 2)\), \( B(2, 3)\), \( C(3, 5)\):

Scrivo il sistema di equazioni lineari sostituendo x e y con le coordinate di ciascun punto.

$$
\begin{cases}
ax_1^2 + bx_1 + c = y_1 \\ \\
ax_2^2 + bx_2 + c = y_2 \\ \\
ax_3^2 + bx_3 + c = y_3 \\
\end{cases} $$

$$
\begin{cases}
a(1^2) + b(1) + c = 2 \\ \\
a(2^2) + b(2) + c = 3 \\ \\
a(3^2) + b(3) + c = 5 \\
\end{cases} $$

$$
\begin{cases}
a + b + c = 2 \\ \\
4a + 2b + c = 3 \\ \\
9a + 3b + c = 5 \\
\end{cases} $$

A questo punto devo risolvere il sistema lineare per trovare i valori \( a \), \( b \), e \( c \) che soddisfano il sistema di equazioni. Per farlo posso scegliere la tecnica che preferisco.

In questo caso opto per il metodo di Cramer.

Nota. In ogni caso, qualsiasi altra tecnica risolutiva di un sistema di equazioni sarebbe andata bene.

Scrivo il sistema in forma matriciale

$$
\begin{pmatrix}
1 & 1 & 1 \\
4 & 2 & 1 \\
9 & 3 & 1 \\
\end{pmatrix}
\begin{pmatrix}
a \\
b \\
c \\
\end{pmatrix}
=
\begin{pmatrix}
2 \\
3 \\
5 \\
\end{pmatrix} $$

Il determinante della matrice dei coefficienti è

$$ \Delta = \begin{vmatrix}
1 & 1 & 1 \\
4 & 2 & 1 \\
9 & 3 & 1 \end{vmatrix} = 1 \cdot \begin{vmatrix} 2 & 1 \\ 3 & 1 \end{vmatrix} - 1 \cdot \begin{vmatrix} 4 & 1 \\ 9 & 1 \end{vmatrix} + 1 \cdot \begin{vmatrix} 4 & 2 \\ 9 & 3 \end{vmatrix} = -1 + 5 -6 = -2 $$

Ora calcolo i determinanti delle matrici ottenute sostituendo la colonna di una variabile (a,b,c) con quella dei termini noti (2,3,5) del sistema.

$$ \Delta_a = \begin{vmatrix}
2 & 1 & 1 \\
3 & 2 & 1 \\
5 & 3 & 1 \end{vmatrix} = 2 \cdot \begin{vmatrix} 2 & 1 \\ 3 & 1 \end{vmatrix} - 1 \cdot \begin{vmatrix} 3 & 1 \\ 5 & 1 \end{vmatrix} + 1 \cdot \begin{vmatrix} 3 & 2 \\ 5 & 3 \end{vmatrix} =  -2  + 2 - 1 = -1 $$

$$ \Delta_b = \begin{vmatrix}
1 & 2 & 1 \\
4 & 3 & 1 \\
9 & 5 & 1 \end{vmatrix} = 1 \cdot \begin{vmatrix} 3 & 1 \\ 5 & 1 \end{vmatrix} - 2 \cdot \begin{vmatrix} 4 & 1 \\ 9 & 1 \end{vmatrix} + 1 \cdot \begin{vmatrix} 4 & 3 \\ 9 & 5 \end{vmatrix} = -2 + 10 -7 = 1 $$

$$ \Delta_c = \begin{vmatrix}
1 & 1 & 2 \\
4 & 2 & 3 \\
9 & 3 & 5 \end{vmatrix} = 1 \cdot \begin{vmatrix} 2 & 3 \\ 3 & 5 \end{vmatrix} - 1 \cdot \begin{vmatrix} 4 & 3 \\ 9 & 5 \end{vmatrix} + 2 \cdot \begin{vmatrix} 4 & 2 \\ 9 & 3 \end{vmatrix} = 1+7 -12 = -4 $$

Quindi, le soluzioni del sistema sono:

$$ a = \frac{ \Delta_a  }{ \Delta } = \frac{-1}{-2} = \frac{1}{2} $$

$$ b = \frac{ \Delta_b  }{ \Delta } = \frac{1}{-2} = - \frac{1}{2} $$

$$ c = \frac{ \Delta_c  }{ \Delta } = \frac{-4}{-2} = 2 $$

In questo modo ho trovato i coefficienti dell'equazione della parabola

$$ y = ax^2+bx+c $$

$$ y = \frac{1}{2}x^2- \frac{1}{2}x +2 $$

La parabola passa per i punti del piano \( A(1, 2)\), \( B(2, 3)\), \( C(3, 5)\)

E così via.