Come determinare l'equazione della parabola noto un punto e il fuoco

Per determinare l'equazione di una parabola conoscendo un punto \((x_0, y_0)\) appartenente alla parabola e il fuoco \((x_F, y_F)\) è necessario conoscere anche altre informazioni che facciano dedurre l'orientamento della parabola (es. verticale, orizzontale, aperta sopra o sotto, a destra o a sinistra, ecc.). In genere queste informazioni aggiuntive sono fornite dal problema stesso.

In generale posso  anche lavorare contemporaneamente su più ipotesi.

• Parabola verticale
  L'asse di simmetria è verticale e la direttrice è orizzontale. Può essere aperta in alto o in basso.
• Parabola orizzontale
  L'asse di simmetria è orizzontale e la direttrice è verticale. Può essere aperta a destra o a sinistra.

Esempio pratico

Considero un punto \((1, 2)\) e il fuoco \((4, 6)\).

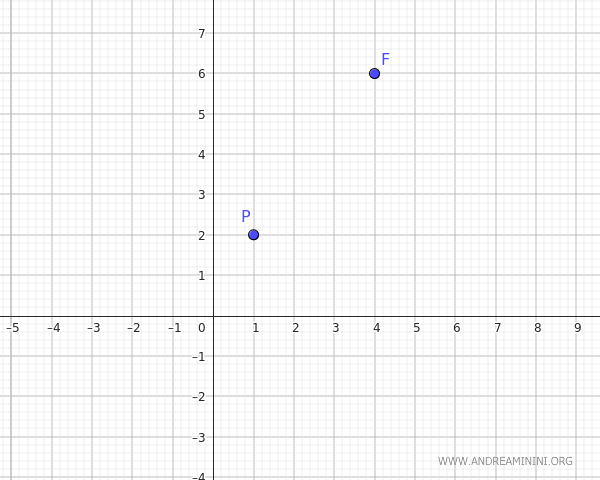
A questo punto faccio due ipotesi: la parabola ha l'asse di simmetria verticale o orizzontale?

La sola conoscenza di un punto e del fuoco non mi consente di dedurre l'orientamento della parabola. Quindi, se il problema non mi fornisce altre informazioni lavoro su entrambe.

1] Parabola con asse di simmetria verticale

Conosco le coordinate di un punto \P((x_0,y_0)=(1, 2)\) della parabola e del il fuoco \((x_F,y_F)=(4, 6)\) e per ipotesi la parabola ha un asse di simmetria verticale.

Sapendo che il fuoco e il vertice sono due punti dell'asse di simmetria, se l'asse di simmetria è verticale deduco che condividano la stessa ascissa $ (h, k) = (4,k) $.  Quindi $ h = 4 $

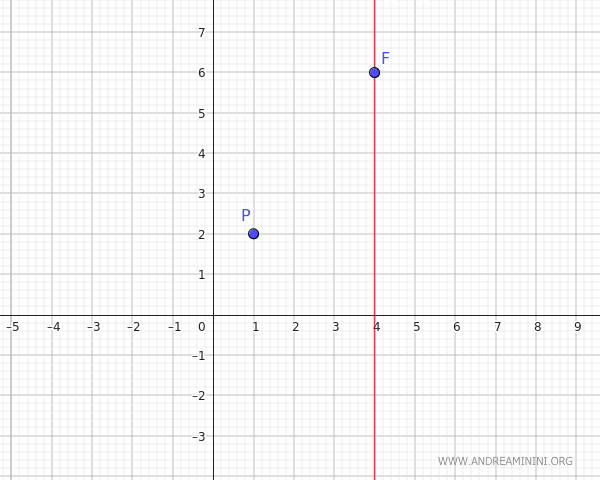
L'equazione generale di una parabola con asse di simmetria verticale è

$$ (x - h)^2 = 4p(y - k) $$

Dove \((h, k)\) è il vertice e \(p\) è la distanza tra il vertice della parabola e il fuoco.

Sapendo che l'asse di simmetria è verticale e che il vertice è $ (h, k) = (4,k) $

$$ (x - 4)^2 = 4p(y - k) $$

In una parabola la distanza tra un punto P è il fuoco è uguale alla distanza tra lo stesso punto P e la direttrice.

Calcolo la distanza tra il punto $ P(1,2) $ e il fuoco ((x_F,y_F)=(4, 6)\)

$$ d_1 = \sqrt{(x_0 - x_F)^2 + (y_0 - y_F)^2} $$

$$ d_1 = \sqrt{(1 - 4)^2 + (2 - 6)^2} $$

$$ d_1 = \sqrt{(-3)^2 + (-4)^2} $$

$$ d_1 = \sqrt{9 + 16} $$

$$ d_1 = \sqrt{25} $$

$$ d_1 = 5 $$

La distanza tra il punto P e il fuoco F è uguale a 5.

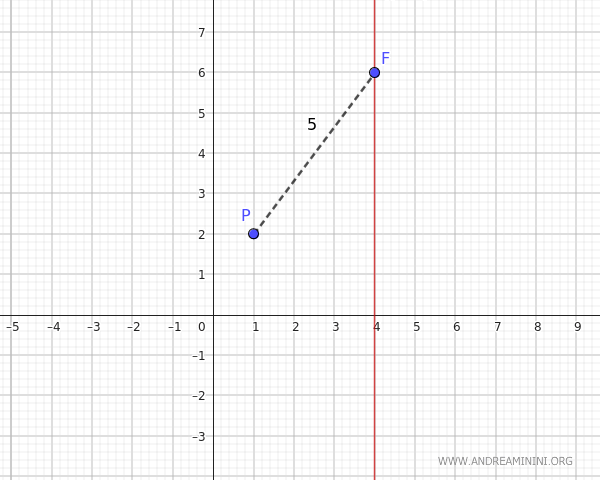
Sapendo che l'asse di simmetria della parabola è verticale e passa per il fuoco $ (4,6 ) $, l'asse ha la stessa ascissa del fuoco

$$ x = x_F $$

$$ x = 4 $$

La retta parallela all'asse di simmetria $ x = 4 $ che passa per il punto $ P(1,2) $ ha la stessa ascissa del punto ovvero è $ x_p=1 $

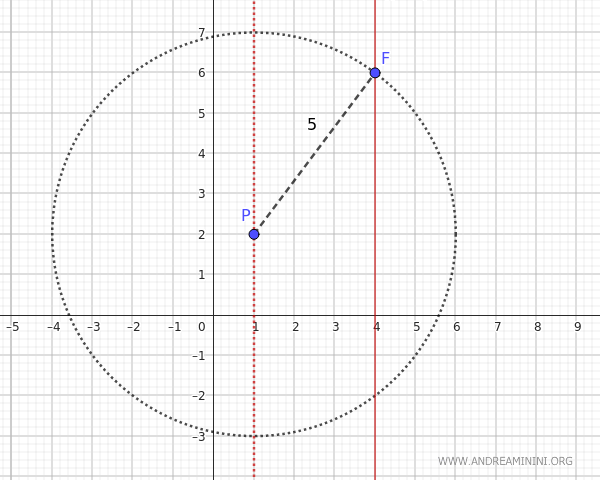
A questo punto, per trovare la direttrice trovo i punti di intersezione tra l'asse $ x_P=1 $ e una circonferenza centrata in $ P(1,2) $ con raggio $ d_1 = 5 $$

$$ \begin{cases} x = x_P   \\ \\ (x-x_P)^2 + (y-y_P)^2 = d_1^2 \end{cases} $$

$$ \begin{cases} x = x_P   \\ \\ (x-1)^2 + (y-2)^2 = 5^2 \end{cases} $$

$$ \begin{cases} x = x_P   \\ \\ (1-1)^2 + (y-2)^2 = 25 \end{cases} $$

$$ \begin{cases} x = x_P   \\ \\  (y-2)^2 = 25 \end{cases} $$

$$ \begin{cases} x = x_P   \\ \\  y^2-4y+4 = 25 \end{cases} $$

$$ \begin{cases} x = x_P   \\ \\  y^2-4y-21 = 0 \end{cases} $$

L'equazione di 2° grado ha due soluzioni

$$ y = \frac{-b \pm \sqrt{b^2-4ac} }{2a} $$

$$ y = \frac{-(-4) \pm \sqrt{(-4)^2-4 \cdot 1 \cdot (-21)} }{2 \cdot 1} $$

$$ y = \frac{4 \pm \sqrt{16+84} }{2} $$

$$ y = \frac{4 \pm \sqrt{100} }{2} $$

$$ y = \frac{4 \pm 10 }{2} $$

$$ y = 2 \pm 5 = \begin{cases} x= 2+5 = 7\\ \\ x = 2-5 = -3 \end{cases} $$

Quindi, la retta direttrice della parabola può essere

$$ y_D= 7  \text{ oppure  } y_D = -3 $$

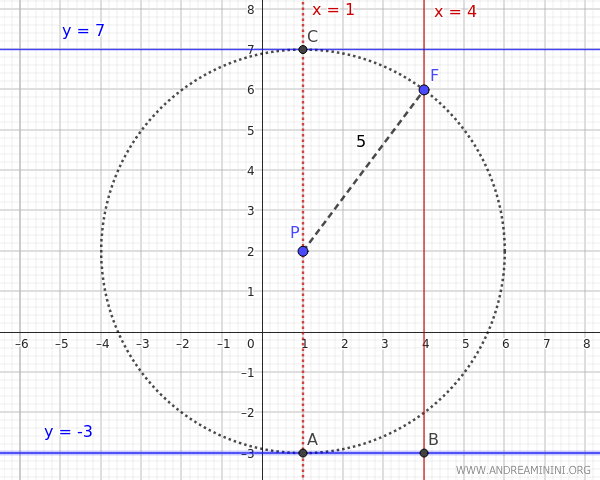
Analizzo le due ipotesi

• Se $ y_D = 7 $ il punto medio tra il fuoco $ F (x_F,y_F)=(4,6) $ e la direttrice $ y_D = 7 $ è il vertice della parabola che si trova alle coordinate $$ V(h,k) = (4, \frac{6+7}{2}) = (4, 6.5) $$ Pertanto, la distanza tra il fuoco e il vertice è $$ p = y_F - k = 6- 6.5 = -0.5 $$ Quindi, l'equazione della parabola è: $$ (x - 4)^2 = 4p(y - k) $$ $$ (x - 4)^2 = 4 \cdot (-0.5) \cdot (y - 6,5) $$ $$ (x - 4)^2 = -2 (y - 6,5) $$
  
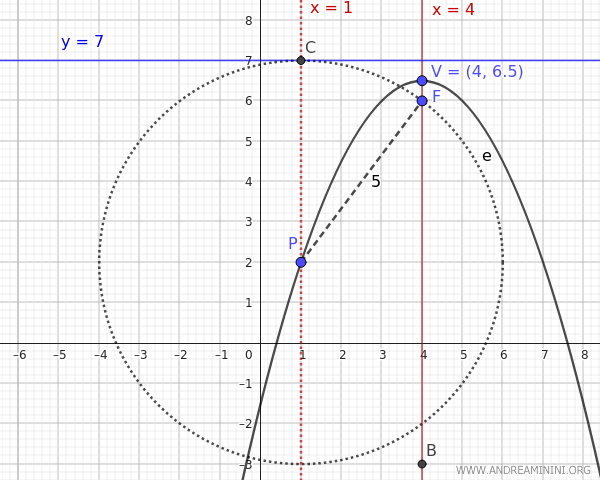
• Se $ y_D = -3 $ il punto medio tra il fuoco $ F (x_F,y_F)=(4,6) $ e la direttrice $ y_D = -3 $ è il vertice della parabola che si trova alle coordinate $$ V(h,k) = (4, \frac{6+(-3)}{2}) = (4,1.5) $$ Pertanto, la distanza tra il fuoco e il vertice è $$ p = y_F - k = 6- 1.5  = 4.5 $$  Quindi, l'equazione della parabola è: $$ (x - 4)^2 = 4p(y - k) $$ $$ (x - 4)^2 = 4 \cdot 4.5 \cdot (y - 1,5) $$ $$ (x - 4)^2 = 18 (y - 1,5) $$
  

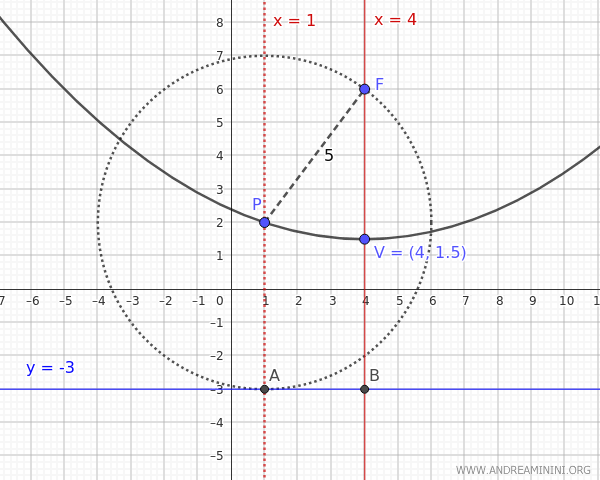
In assenza di altre informazioni entrambe le ipotesi sono possibili, sia la parabola con l'apertura verso l'alto che quella con l'apertura verso il basso.

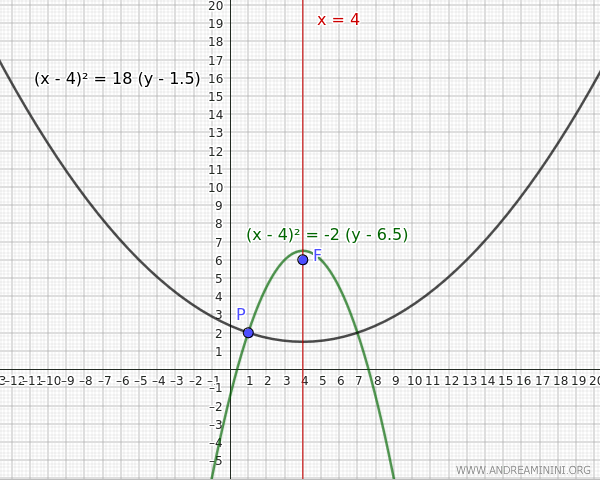
2] Parabola con asse di simmetria orizzontale

Le coordinate del punto sono \( P(x_0,y_0)=(1, 2)\) mentre quelle del fuoco della parabola sono \((x_F,y_F)=(4, 6)\) e per ipotesi la parabola ha un asse di simmetria orizzontale.

L'equazione di una parabola con l'asse di simmetria parallelo all'asse x è.

$$ (y-k)^2 = 4p(x-h) $$

Sapendo che il fuoco e il vertice sono due punti dell'asse di simmetria, se l'asse di simmetria è orizzontale deduco che condividono la stessa ordinata $ (h, k) = (h,6) $.  Quindi $ k = 6 $

$$ (y-6)^2 = 4p(x-h) $$

Poiché il punto \( P(x_0,y_0)=(1, 2) \) è un punto della parabola, allora soddisfa l'equazione.

Quindi, posso sostituire le coordinate x=1 e y=2 nell'equazione della parabola.

$$ (2-6)^2 = 4p(1-h) $$

$$ (-4)^2 = 4p(1-h) $$

$$ 16 = 4p(1-h) $$

Il parametro p è la distanza tra il fuoco e il vertice $ p = x_F - h $ sull'asse di simmetria orizzontale dove $ x_F= 4 $.

$$ p = x_F - h = 4 - h $$

Sostituisco $ p $ con $ 4-h $ nell'equazione della parabola.

$$ 16 = 4 \cdot (4-h) \cdot (1-h) $$

$$ 16 = 4 \cdot (  4 - 4h - h + h^2 ) $$

$$ 16 = 4 \cdot (  4 - 5h + h^2 ) $$

$$ 16 = 16 - 20h + 4h^2 $$

$$ 4h^2- 20h = 0 $$

$$ h \cdot (4h-20) = 0 $$

Questa equazione di 2° grado ha due soluzioni $ h = 0 $ e $ h = 5 $

Quindi, devo valutare entrambe le ipotesi:

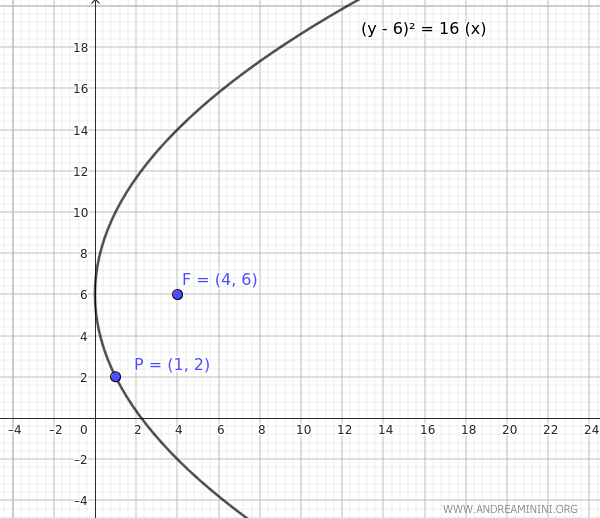
• Se $ h = 0 $ allora la distanza tra il fuoco e il vertice è $ p = 4-h = 4-0 = 4 $ Quindi, l'equazione della parabola con $ h = 0 $ e $ p = 4 $ diventa: $$ (y-6)^2 = 4p(x-h) $$ $$ (y-6)^2 = 4 \cdot 4 \cdot (x-0) $$ $$ (y-6)^2 = 16 (x-0) $$ Poiché p>0 la parabola è aperta a destra.
  
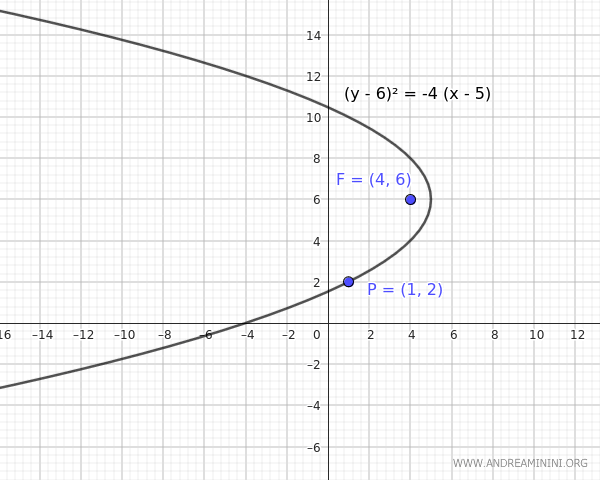
• Se $ h = 5 $ allora la distanza tra il fuoco e il vertice è $ p = 4-h = 4-5 = -1 $ Quindi, l'equazione della parabola con $ h = 5 $ e $ p = -1 $ diventa: $$ (y-6)^2 = 4p(x-h) $$ $$ (y-6)^2 = 4 \cdot (-1) \cdot (x-5) $$ $$ (y-6)^2 = -4 (x-5) $$ Poiché p<0 la parabola è aperta a sinistra.
   

In assenza di altre informazioni entrambe le soluzioni sono valide.

E così via.