Teorema dell'area del segmento parabolico di Archimede
L'area $ S $ di un segmento parabolico, cioè la regione delimitata da una parabola e da una corda AB che non è l'asse di simmetria, è uguale a 2/3 dell'area $ A $ del rettangolo ABDC costruito sulla retta tangente alla parabola e parallela alla corda. $$ S = \frac{2}{3} \times A $$
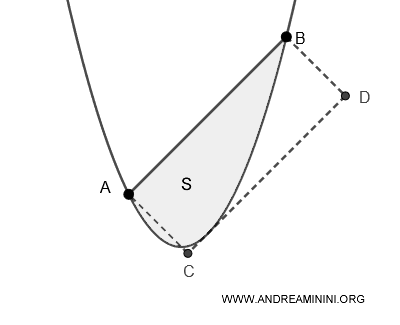
In alternativa, si può anche dire che l'area del segmento parabolico è equivalente ai 4/3 dell'area del triangolo inscritto ABC nel segmento parabolico che ha per base la corda AB e come vertice opposto C il punto di tangenza alla parabola della retta parallela alla corda.
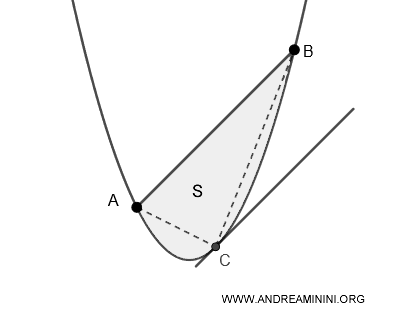
Se il triangolo inscritto ha area \( A \), allora l'area \( S \) del segmento parabolico è data da:
$$ S = \frac{4}{3} \times A $$
Questa formula restituisce un risultato sorprendentemente preciso per l'epoca, e dimostra l'ingegnosità dei metodi geometrici di Archimede.
Nota. Per determinare l'area del segmento parabolico in modo preciso dovrei integrare direttamente la funzione che descrive la parabola. Il teorema di Archimede mi fornisce un metodo di calcolo numerico alternativo che non richiede l'utilizzo degli strumenti di analisi matematica.
Esempio pratico
Considero una semplice parabola
$$ y = x^2 $$
Poi traccio una corda AB che ha come estremi i punti A(-1;1) e B(2;4)
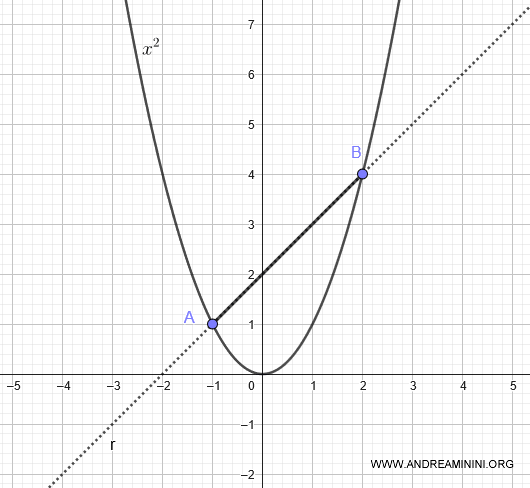
Devo calcolare l'area della superficie sotto la corda AB all'interno della parabola.
Per farlo utilizzo il metodo di Archimede. Trovo la retta parallela al segmento AB che sia anche tangente alla parabola.
Il segmento AB si trova sulla retta r
$$ y = x+2 $$
Il fascio delle rette parallele alla retta r è il seguente:
$$ y = mx + q $$
I punti di intersezione tra la parabola $ y = x^2 $ e il fascio di rette $ y = x+q $ sono dati da
$$ x^2 = mx+q $$
Tra questi devo trovare qual'è la retta tangente alla parabola.
Riscrivo l'equazione del fascio di rette nella forma generale
$$ y - mx - q = 0 $$
Affinché la retta sia tangente, il discriminante di questa equazione deve essere zero.
$$ \Delta = 0 $$
Il discriminante è dato da:
$$ \Delta = b^2 - 4ac = 0 $$
In questo caso la retta è $ y - x - q = 0 $ dove a=1, b=-m e c=-q
$$ \Delta = (-m)^2 - 4 \cdot 1 \cdot (-q) = 0 $$
$$m^2 + 4q= 0 $$
Da questa ricavo $ q $
$$ q= - \frac{m^2}{4} $$
Quindi, la retta tangente alla parabola e parallela alla corda AB è
$$ y = mx + q $$
$$ y = mx - \frac{m^2}{4} $$
Il coefficiente angolare $ m $ nella retta $ y=x+2 $ che comprende la corda AB è $ m=1 $
$$ y = 1 \cdot x - \frac{1^2}{4} $$
$$ y = x - \frac{1}{4} $$
Quest'ultima è la retta tangente alla parabola $ y=x^2 $ e parallela alla corda AB.
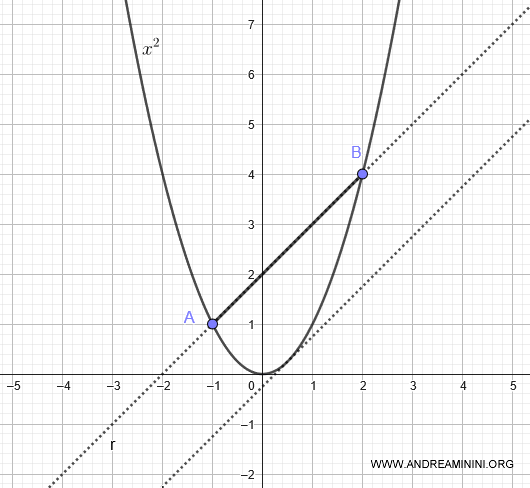
Traccio due segmenti perpendicolari tra la retta r e la retta tangente che hanno come estremi i punti A e B.
In questo modo ottengo un rettangolo ABCD.
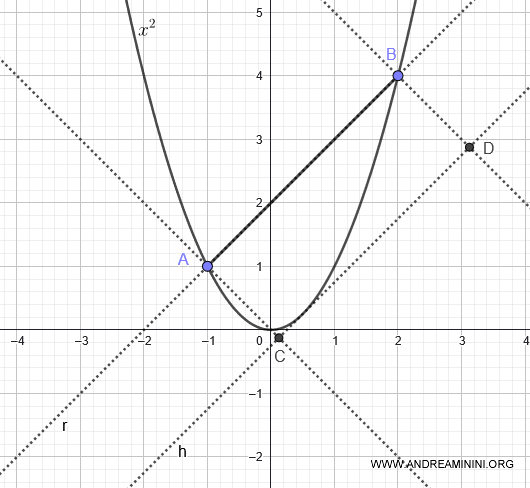
Secondo il teorema di Archimede i 2/3 dell'area del rettangolo ABCD sono equivalenti all'area della parabola sotto la corda AB.
Per misurare la lunghezza del lato AB del rettangolo calcolo la distanza tra i punti A e B
$$ \overline{AB} = \sqrt{(x_B-x_A)^2+(y_B-y_A)^2} $$
Dove A(-1;1) e B(2;4)
$$ \overline{AB} = \sqrt{(2-(-1))^2+(4-1)^2} $$
$$ \overline{AB} = \sqrt{3^2+(3)^2} $$
$$ \overline{AB} = \sqrt{9+9} $$
$$ \overline{AB} = \sqrt{18} $$
Per misurare la lunghezza del lato AC del rettangolo calcolo la distanza tra il punto A(-1;1) e la retta tangente $ y=x- \frac{1}{4} $
$$ \overline{AC} = \frac{|ax+by+c|}{ \sqrt{a^2+b^2} } $$
Sapendo che la retta è tangente è $ y=x- \frac{1}{4} $ ovvero $ - x+y+ \frac{1}{4} = 0 $ ottengo i coefficienti a=-1, b=-1 e c=1/4
$$ \overline{AC} = \frac{|-1 \cdot x+ 1 \cdot y+ \frac{1}{4}|}{ \sqrt{(-1)^2+1^2} } $$
$$ \overline{AC} = \frac{|-x + y+ \frac{1}{4}|}{ \sqrt{2 } } $$
Sostituisco x e y con le coordinate del punto A(-1;1)
$$ \overline{AC} = \frac{|-(-1) + 1 + \frac{1}{4}|}{ \sqrt{2 } } $$
$$ \overline{AC} = \frac{|1 + 1 + \frac{1}{4}|}{ \sqrt{2 } } $$
$$ \overline{AC} = \frac{| \frac{4+4+1}{4}|}{ \sqrt{2 } } $$
$$ \overline{AC} = \frac{| \frac{9}{4}|}{ \sqrt{2 } } $$
$$ \overline{AC} = \frac{9}{4} \cdot \frac{1}{\sqrt{2}} $$
$$ \overline{AC} = \frac{9}{4 \cdot \sqrt{2} } $$
A questo punto posso calcolare l'area A del rettangolo ABCD
$$ A = \overline{AB} \cdot \overline{AC} $$
$$ A = \sqrt{18} \cdot \frac{9}{4 \cdot \sqrt{2} } $$
$$ A = \sqrt{2 \cdot 3^2} \cdot \frac{9}{4 \cdot \sqrt{2} } $$
$$ A = 3 \cdot \sqrt{2} \cdot \frac{9}{4 \cdot \sqrt{2} } $$
$$ A = 3 \cdot \frac{9}{4} $$
$$ A = \frac{27}{4} $$
In base al teorema di Archimede, l'area sotto la corda AB è pari a 2/3 dell'area del rettangolo ABCD.
$$ S = \frac{2}{3} \cdot A $$
$$ S = \frac{2}{3} \cdot \frac{27}{4} $$
$$ S = \frac{1}{3} \cdot \frac{27}{2} $$
$$ S = \frac{27}{6} $$
$$ S \approx 4.5 $$
Quindi, l'area tra la corda AB e la parabola è 4.5
Verifica. Per verificare il risultato calcolo l'area tra la corda AB e l'asse x.
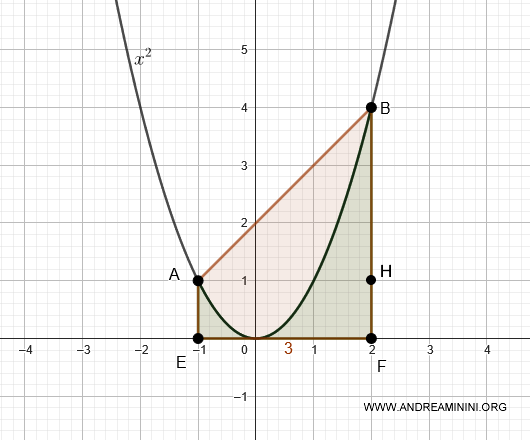
L'area AEFB è composta dall'area di un triangolo AHF di base 3 e altezza 3 e l'area di un rettangolo AEFH di base 3 e altezza 1.
$$ Area(AEFB) = Area(AHF) + Area (AEFH) $$
$$ Area(AEFB) = \frac{3 \cdot 3}{2} + 3 \cdot 1 $$
$$ Area(AEFB) = \frac{9}{2} + 3 $$
$$ Area(AEFB) = \frac{9+6}{2} $$
$$ Area(AEFB) = \frac{15}{2} $$
$$ Area(AEFB) = 7.5 $$
L'area tra la parabola e l'asse x (di colore verde) si ottiene tramite l'integrale della funzione $ x^2 $ tra gli estremi $ a=-1 $ e $ b=2 $
$$ \int_a^b x^2 \ dx $$
Dove a=-1 e b=2 sono gli estremi della corda AB sull'asse x.
$$ \int_{-1}^2 x^2 \ dx $$
L'integrale di $ x^2 $ è la funzione $ \frac{x^3}{3} $ quindi l'integrale è
$$ \int_{-1}^2 x^2 \ dx = | \frac{x^3}{3} |_{-1}^2 $$
$$ \frac{2^3}{3} - \frac{(-1)^3}{3} $$
$$ \frac{8}{3} + \frac{1}{3} $$
$$ \frac{9}{3} = 3 $$
Quindi l'area sotto la parabola è uguale a 3
$$ \int_{-1}^2 x^2 \ dx = 3 $$
L'area S tra la corda AB e la parabola $ x^2 $ è uguale alla differenza tra l'area AEFB e l'area sotto la parabola (ovvero l'integrale).
$$ S = Area(AEFB) - \int_{-1}^2 x^2 \ dx $$
L'area AEFB è uguale a 7.5 mentre l'integrale è uguale a 3.
$$ S = 7.5 - 3 $$
$$ S = 4.5 $$
Il risultato finale è lo stesso ottenuto tramite il metodo di Archimede. L'area tra la corda AB e la parabola è 4.5.
Dimostrazione
Considero un segmento parabolico, cioè la regione delimitata da una parabola e da una corda AB che collega due punti della parabola.
Costruisco un triangolo inscritto ABC formato dalla corda AB e dal punto C della parabola che si trova sulla perpendicolare alla corda passante per il punto medio M della stessa.
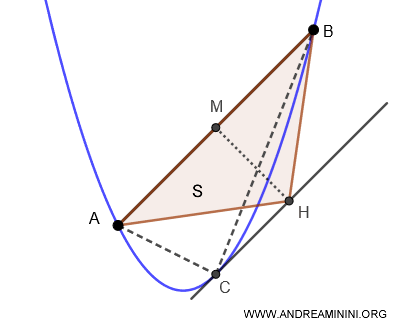
Per verificare il risultato Archimede utilizzo un calcolo per approssimazione tramite una tecnica che oggi chiameremmo "metodo di esaustione", un precursore del calcolo integrale.
Suddivise il segmento parabolico in una serie di triangoli più piccoli, dimostrando che l'area totale di questi triangoli tende al valore vero dell'area del segmento parabolico.
E così via.
