Il segmento parabolico

Il segmento parabolico è quella parte di piano delimitata da un arco di parabola e dalla corda che lo chiude.

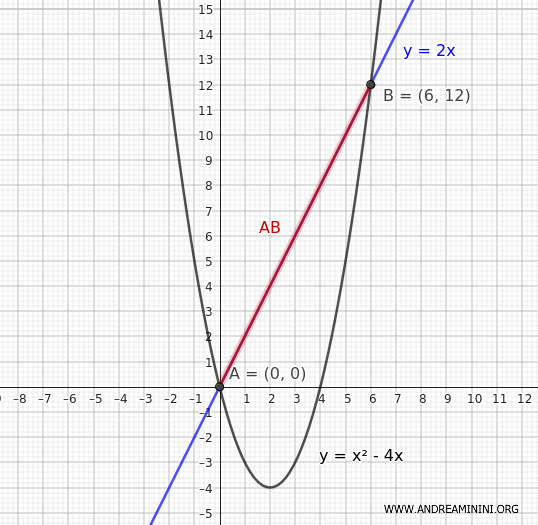
Considero una retta secante che interseca la parabola nei punti A e B.

L'area tra la corda AB e l'arco di parabola AB è detto segmento parabolico.

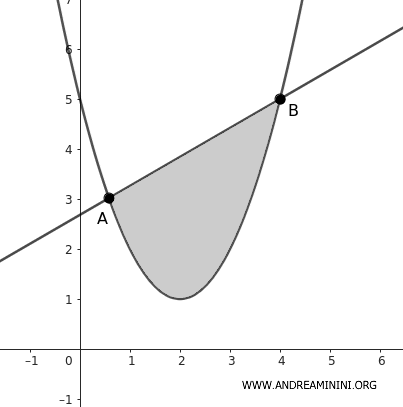
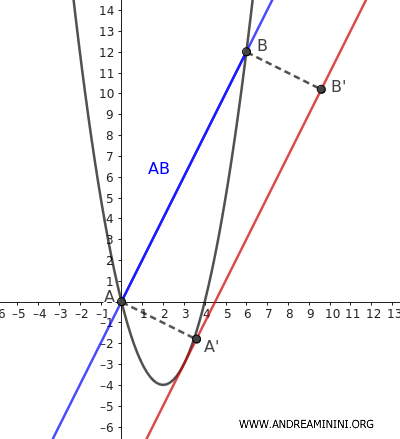
Una proprietà interessante è che l'area del segmento parabolico è pari ai 2/3​ dell'area del rettangolo ABB'A' ottenuto proiettando i punti AB sulla retta tangente alla parabola e parallela alla corda.

$$A_s = \frac{2}{3} ( \overline{AB} \cdot \overline{AA'} )$$

Questa proprietà deriva dal Teorema di Archimede, in quanto è stata dimostrata per la prima volta dal matematico greco nel III secolo a.C.

In alternativa, l'area del segmento parabolico può essere calcolata anche ricorrendo al calcolo integrale.

L'area del segmento parabolico

La formula per calcolare l'area del segmento parabolico è un po' meno ovvia rispetto a quella per un cerchio.

Se ho una parabola con equazione $y = ax^2$ e la corda va da $x = x_1$ a $x = x_2$, con $x_1<x_2$ allora l'area del segmento parabolico è data da:

$$A_s = \frac{a}{3} \cdot (x_2^3-x_1^3)$$

Nota che se la corda va da $x = -k$ a $x = k$ la formua precedente diventa $$A_s = \frac{a}{3} \cdot (k^3-(-k)^3)$$ $$A_s = \frac{a}{3} \cdot (k^3+k^3)$$ $$A_s = \frac{a}{3} \cdot (2k^3)$$ $$A_s = \frac{2}{3} \cdot a \cdot k^3$$

Un esempio pratico

Considero una parabola

$$y = x^2-4x$$

e una retta secante

$$y = 2x$$

Devo calcolare l'area del segmento di parabola.

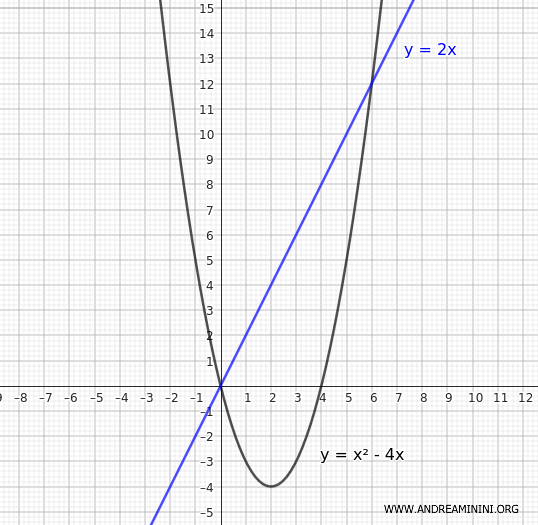
Per prima cosa trovo i punti di intersezione, ovvero i punti in comune tra la parabola e la retta secante

$$\begin{cases} y = x^2-4x \\ \\ y = 2x \end{cases}$$

$$\begin{cases} y = x^2-4x \\ \\ x^2-4x = 2x \end{cases}$$

$$\begin{cases} y = x^2-4x \\ \\ x^2-4x-2x = 0 \end{cases}$$

$$\begin{cases} y = x^2-4x \\ \\ x^2-6x = 0 \end{cases}$$

$$\begin{cases} y = x^2-4x \\ \\ x(x-6) = 0 \end{cases}$$

La seconda equazione si risolve per x=0 e x=6

$$x = \begin{cases} x_1=0 \\ \\ x_2=6 \end{cases}$$

Sostituisco x₁=0 e x₂=6 nell'equazione della retta $y=2x$ per trovare la componente y delle coordinate

$$y_1=2 x_1 = 2 \cdot 0 = 0$$

$$y_2=2 x_2 = 2 \cdot 6 = 12$$

Quindi, i punti di intersezione tra la retta e la parabola si trovano alle coordinate A(x₁;y₁)=(0;0) e B(x₂;y₂)=(6;12)

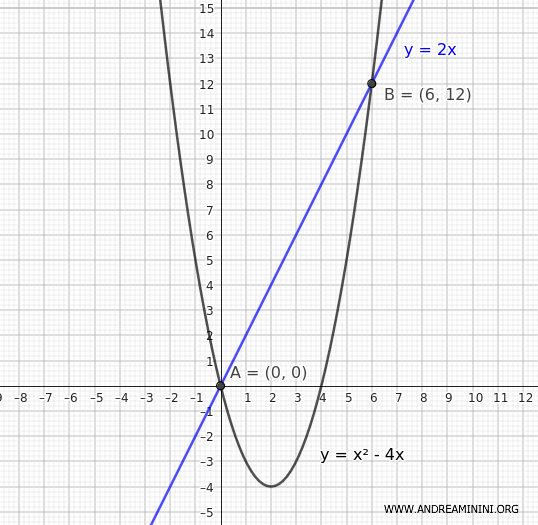
Ora misuro la distanza tra gli estremi della corda

$$\overline{AB} = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$

$$\overline{AB} = \sqrt{(6-0)^2+(12-0)^2}$$

$$\overline{AB} = \sqrt{6^2+12^2}$$

$$\overline{AB} = \sqrt{36+144}$$

$$\overline{AB} = \sqrt{180}$$

$$\overline{AB} = \sqrt{2^2 \cdot 3^2 \cdot 5}$$

$$\overline{AB} = 2 \cdot 3 \cdot \sqrt{5}$$

$$\overline{AB} = 6\cdot \sqrt{5}$$

Quindi, la lunghezza della corda $\overline{AB}$ misura $6\cdot \sqrt{5}$

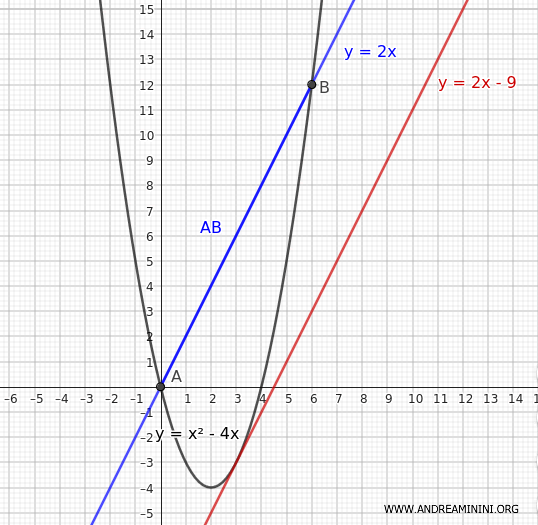
Trovo l'equazione di una retta parallela a $y=2x$ che sia tangente con la parabola $y=x^2-4x$$

L'equazione della retta parallela a $y=2x$ è :

$$y = 2x+q$$

La condizione di tangenza tra una retta e una parabola si ottiene eguagliando le equazioni e ponendo come condizione di tangenza il discriminante nullo $\Delta=0$

$$2x+q = x^2-4x$$

$$x^2-4x-2x - q = 0$$

$$x^2-6x - q = 0$$

Devo trovare il valore che rende nullo il discriminante di quest'ultima equazione di 2° grado.

$$\Delta = b^2-4ac = 0$$

In questo caso a=1, b=-6 e c=-q

$$\Delta = b^2 -4ac = 0$$

$$(-6)^2-4 \cdot 1 \cdot (-q) = 0$$

$$36+ 4q = 0$$

$$q = \frac{-36}{4} = -9$$

Quindi, l'equazione parallela alla retta $y=2x$ e tangente alla parabola $y=x^2-4x$ ha come termine noto q=-9

$$y = 2x + q$$

$$y = 2x -9$$

Calcolo la distanza tra la retta $y=2x$ e la retta parallela $y=2x-9$$

$$d = \frac{|c_2-c_1|}{\sqrt{1+m^2}}$$

Dove i termini noti sono c₁=0 e c₂=-9 mentre il coefficiente angolare delle due rette è m=2.

$$d = \frac{|-9-0|}{\sqrt{1+2^2}}$$

$$d = \frac{9}{\sqrt{5}}$$

Verifica. Prendo un punto qualsiasi della retta $y-2x = 0$ ad esempio P(x₀;y₀)=(0;0). Poi calcolo la distanza del punto P(0;0) dalla retta parallela $y - 2x+9 =0$ tramite la formula $$d = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$$ Dove a=1, b=-2, c=9 $$d = \frac{|1 \cdot 0+(-2) \cdot 0+9|}{\sqrt{1^2+(-2)^2}}$$ $$d = \frac{9}{\sqrt{5}}$$

Quindi la distanza tra le due rette è $d = \overline{AA'} = \overline{BB'} = \frac{9}{\sqrt{5}}$

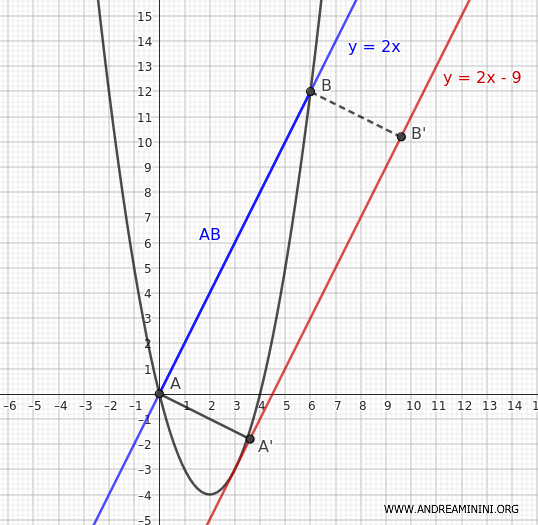
A questo punto conosco la base AB e l'altezza d=AA' del rettangolo ABB'A'

$$\overline{AB} = 6\cdot \sqrt{5}$$

$$\overline{AA'} = \frac{9}{\sqrt{5}}$$

Sapendo che l'area del segmento parabolico è 2/3 dell'area del rettangolo ABB'A'

$$A_s = \frac{2}{3} \cdot ( \overline{AB} \cdot \overline{AA'} )$$

$$A_s = \frac{2}{3} \cdot  6\cdot \sqrt{5} \cdot \frac{9}{\sqrt{5}}$$

$$A_s = \frac{2}{3} \cdot 6 \cdot 9$$

$$A_s = \frac{2}{3} \cdot 54$$

$$A_s = 36$$

Quindi, l'area del segmento parabolico è 36.

Soluzione alternativa

Lo stesso problema precedente avrei potuto risolverlo utilizzando la formula

$$A_s = \frac{a}{3} \cdot (x_2^3-x_1^3)$$

Dove j e k sono la componente x del primo e del secondo punto di intersezione tra la corda e la parabola.

Considero una parabola

$$y = x^2-4x$$

e una retta secante

$$y = 2x$$

I punti di intersezione della parabola e la retta secante li ho già calcolati nell'esempio precedente, si trovano alle coordinate A(x₁;y₁)=(0;0) e B(x₂;y₂)=(6;12)

A questo punto applico la formula indicando x₁=0 e x₂=6

$$A_s = \frac{a}{3} \cdot (6^3-0^3)$$

$$A_s = \frac{a}{3} \cdot (108)$$

L'equazione generale retta secante è $y-2x=0$, quindi il coefficiente $a=1$

$$A_s = \frac{1}{3} \cdot (108)$$

$$A_s = 36$$

L'area del segmento parabolico è 36, il risultato è lo stesso.

Il calcolo dell'area del segmento parabolico tramite gli integrali

L'area del segmento parabolico si può calcolare anche utilizzando l'integrale.

L'area del segmento parabolico è uguale alla differenza tra l'area del trapezio ABCD formata dalla corda AB e dall'asse $x$ e l'integrale della parabola tra $x_1$ e $x_2$ $$Area(segmento) = Area(ABCD) -   \int_{x_1}^{x_2}  ax^2+bx+c$$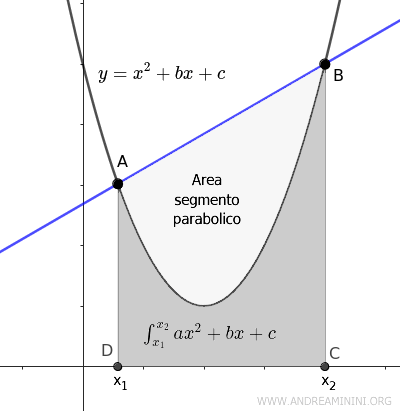

In generale, l'integrale della parabola calcola l'area tra la parabola e l'ascissa quando la parabola si trova nel semiasse y positivo.

Quindi, l'area del segmento parabolico si può ottenere per differenza dall'area del trapezio ABCD.

Nota. Il calcolo del segmento parabolico tramite l'integrale è corretto anche quando la parabola si trova parzialmente nel semiasse y negativo. In questo caso l'integrale calcola la differenza tra la superficie tra la parabola e l'ascisse nel semiasse delle ordinate positivo e negativo. Nel prossimo esempio farò un esempio pratico di questo caso.

Esempio

Considero la parabola $y = x^2 - 4x$ e la retta secante $y = 2x$. La retta interseca la parabola alle coordinate $A(x_1, y_1) = (0, 0)$ e $B(x_2, y_2) = (6, 12)$.

A questo punto calcoliamo l'area del segmento parabolico per differenza tra l'area del trapezio e l'area sotto la parabola.

1] Calcolo l'area del trapezio

L'area del trapezio $A_{\text{trapezio}}$ è data dalla base media moltiplicata per l'altezza diviso due:

$$A_{\text{trapezio}} = \frac{(b_1+b_2) \cdot h}{2}$$

La base minore è b1=y1=0, la base maggiore è b2=y2=12, l'altezza è x2-x1=6-0=0.

$$A_{\text{trapezio}} = \frac{(0+12) \cdot 6}{2}$$

$$A_{\text{trapezio}} = 36$$

Quindi, l'area del trapezio è 36

Da notare che in questo caso particolare il trapezio formato tra la corda e l'asse x degenera in un semplice triangolo ABC

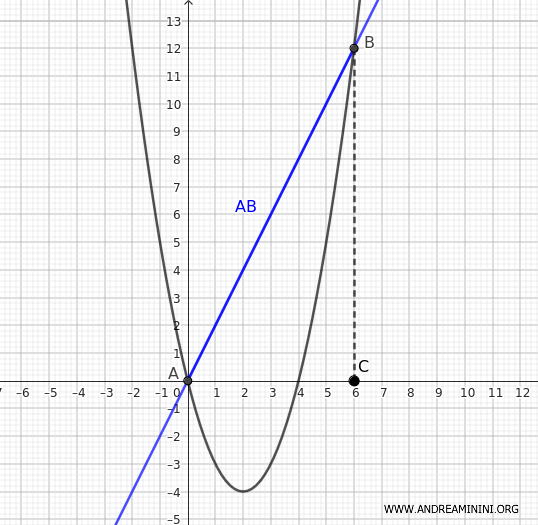
2] Calcolo l'area sotto la parabola

Per calcolare l'area sotto la parabola $y = x^2 - 4x$ tra $x_1 = 0$ e $x_2 = 6$, devo integrare la funzione:

$$A_{\text{parabola}} = \int_{0}^{6} (x^2 - 4x) \, dx$$

Calcolo l'integrale:

$$A_{\text{parabola}} = \int_{0}^{6} x^2 \, dx - \int_{0}^{6} 4x \, dx$$

L'integrale di $x^2$ è $\frac{x^3}{3}$ e l'integrale di $4x$ è $2x^2$:

$$A_{\text{parabola}} = \left[ \frac{x^3}{3} \right]_{0}^{6} - \left[ 2x^2 \right]_{0}^{6}$$

Calcolo i valori:

$$\left[ \frac{x^3}{3} \right]_{0}^{6} = \frac{6^3}{3} - \frac{0^3}{3} = \frac{216}{3} = 72$$

$$\left[ 2x^2 \right]_{0}^{6} = 2 \cdot 6^2 - 2 \cdot 0^2 = 2 \cdot 36 = 72$$

Quindi, l'area sotto la parabola è zero

$$A_{\text{parabola}} = 72 - 72 = 0$$

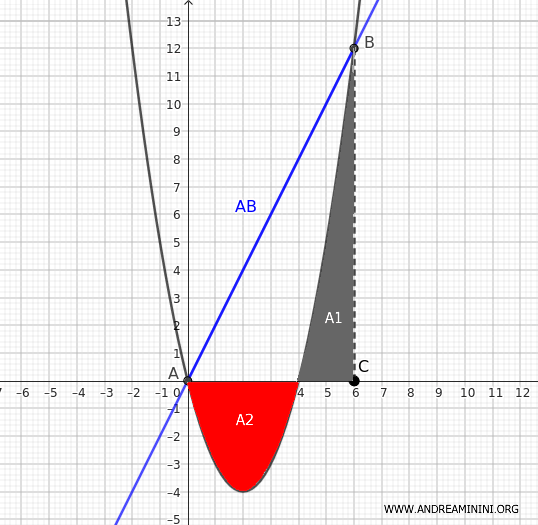
Nota. Quando si calcola l'integrale definito la superficie A1 tra la parabola e l'ascisse nel semiasse y positivo si calcola col il segno più mentre la superficie A2 tra la parabola e l'ascisse nel semiasse y negativo con il segno meno. Quindi, l'integrale definito è uguale alla differenza A1-A2. In questo caso particolare l'integrale definito non misura propriamente l'area sotto la parabola. E' opportuno ricordarsi che l'integrale definito misura l'area sotto la parabola soltanto quando questa si trova sul semiasse y positivo.

3] Calcolo l'area del segmento parabolico

L'area del segmento parabolico è la differenza tra l'area del trapezio e l'integrale della parabola:

$$Area(segmento) = Area(ABCD) -   \int_{x_1}^{x_2}  ax^2+bx+c$$

$$Area(segmento) = 36 - 0 = 36$$

Quindi, l'area del segmento parabolico è $36$. 

E così via.