La formula di sdoppiamento di una parabola
La formula di sdoppiamento di una parabola permette di ottenere l'equazione della retta tangente in un punto $ P(x_0;y_0) $ della parabola. $$ \frac{y+y_0}{2} = ax_0 x + b \left( \frac{x+x_0}{2} \right) + c $$ Dove a, b, c sono i coefficienti della parabola $ y = ax^2+bx+c $
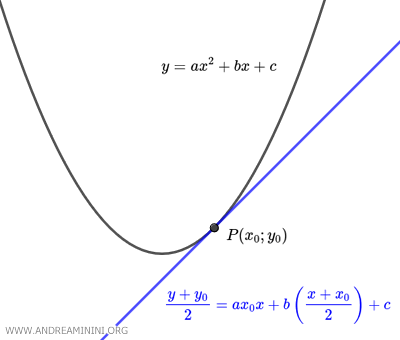
La formula di sdoppiamento posso ottenerla partendo dall'equazione generale di una parabola
$$ y = ax^2+bx+c $$
Sostituisco i termini quadratici e lineari con i seguenti termini formali:
$$ x^2 \rightarrow x_0x $$
$$ x \rightarrow \frac{x+x_0}{2} $$
$$ y \rightarrow \frac{y+y_0}{2} $$
Quindi, l'equazione della parabola diventa:
$$ y = ax^2+bx+c $$
$$ \frac{y+y_0}{2} = ax_0 x + b \left( \frac{x+x_0}{2} \right) + c $$
Nota. La formula di sdoppiamento si applica solo per trovare la retta tangente in un punto della parabola. Non si applica se il punto è esterno alla parabola. In generale, si tratta dell'applicazione particolare della formula di sdoppiamento di una conica al caso della parabola.
Un esempio pratico
Considero una parabola
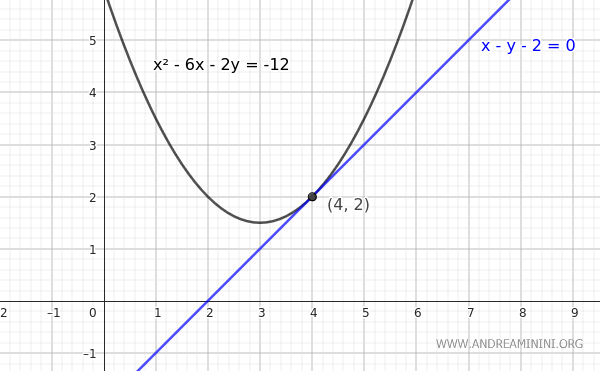
$$ x^2-6x-2y = -12 $$
La scrivo in forma generale
$$ x^2-6x-2y +12 = 0 $$
Voglio trovare l'equazione della retta tangente al punto $ P(4;2) $ della parabola.
Nota. Per prima cosa verifico se il punto P(4;2) si trova effettivamente sulla parabola, sostituendo x=4 e y=2 nell'equazione della parabola. $$ (4)^2-6 \cdot 4-2 \cdot 2 = -12 $$ $$ 16-24-4 = -12 $$ $$ -12 = -12 $$ L'equazione è soddisfatta, quindi P(4;2) è un punto della parabola. A costo di ripetermi, ricordo che la formula di sdoppiamento si applica solo sui punti della parabola. Non si applica sui punti esterni.
Sostituisco il termine quadratico $ x^2 \rightarrow x_0x $ nell'equazione della parabola
$$ x_0x-6x-2y + 12 = 0 $$
Sostituisco il termine lineare $ x \rightarrow \frac{x+x_0}{2} $
$$ x_0x-6 \cdot \frac{x+x_0}{2} -2y + 12 = 0 $$
$$ x_0x-3 \cdot (x+x_0) -2y + 12 = 0 $$
Sostituisco il termine lineare $ y \rightarrow \frac{y+y_0}{2} $
$$ x_0x-3 \cdot (x+x_0) -2 \cdot \frac{y+y_0}{2} + 12 = 0 $$
$$ x_0x-3 \cdot (x+x_0) -y - y_0 + 12 = 0 $$
Il punto di tangenza si trova alle coordinate $ P(4;2) $, quindi $ x_0=4 $ e $ y_0=2 $
$$ 4x-3 \cdot (x+4) -y - 2 + 12 = 0 $$
$$ 4x-3x-12 -y + 10 = 0 $$
$$ x -y - 2 = 0 $$
Quest'ultima è l'equazione della retta tangente alla parabola nel punto P(4;2)
La dimostrazione
Per dimostrare la formula di sdoppiamento della parabola, considero l'equazione generale della parabola
$$ y = ax^2+bx+c $$
Prendo un punto $ P(x_0;y_0 ) $
Il fascio di rette passanti per P è individuato dalla seguente equazione:
$$ y-y_0 = m \cdot (x-x_0) $$
Per ottenere le rette che intersecano la parabola (rette secanti e tangenti) e passano per P costruisco il sistema di equazioni
$$ \begin{cases} y = ax^2+bx+c \\ \\ y = m(x-x_0)+y_0 \end{cases} $$
L'equazione risolvente del sistema è
$$ ax^2+bx+c = m(x-x_0)+y_0 $$
$$ ax^2+bx+c - m(x-x_0)-y_0 = 0 $$
$$ ax^2+bx+c - mx + mx_0-y_0 = 0 $$
$$ ax^2+x(b-m)+ mx_0-y_0 +c = 0 $$
In un'equazione di secondo grado $ Ax^2+Bx+C=0 $ se il discriminante è maggiore di zero $ \Delta>0 $ la somma delle radici x1 e x2 è uguale al rapporto tra i coefficienti -B/A
$$ x_1+x_2 = - \frac{B}{A} $$
Dove A=a e B=(b-m)
$$ x_1+x_2 = - \frac{b-m}{a} $$
In questo caso però mi interessa conoscere solo il punto di tangenza e non i punti di intesezione delle rette secanti.
Quindi, le soluzioni dell'equazione di 2° grado sono coincidenti $ x_1=x_2 $ e sono uguali a $ x_0 $
$$ x_0+x_0 = - \frac{b-m}{a} $$
$$ 2x_0 = - \frac{b-m}{a} $$
Da quest'ultima equazione ricavo il coefficiente angolare m
$$ m = 2ax_0 + b $$
Sostituisco il coefficiente angolare m nell'equazione del fascio di rette.
$$ y-y_0 = m \cdot (x-x_0) $$
$$ y-y_0 = (2ax_0 + b) \cdot (x-x_0) $$
$$ y-y_0 = 2ax_0x - 2ax_0^2 +bx-bx_0 $$
Sapendo che il punto $ P(x_0;y_0) $ è un punto della parabola, posso sostituire $ x_0 $ e $ y_0 $ nell'equazione della parabola.
$$ y_0 = ax_0^2+bx_0+c $$
Moltiplico per due entrambi i membri
$$ 2y_0 = 2ax_0^2+2bx_0+2c $$
Sommo membro a membro le due equazioni $ y-y_0 = m \cdot (x-x_0) $ e $ 2y_0 = 2ax_0^2+2bx_0+2c $
\[
\begin{array}{rcl}
y - y_0 & = & 2ax_0 x - 2ax_0^2 + bx - bx_0 \\
2y_0 & = & 2ax_0^2 + 2bx_0 + 2c \\
\hline
y + y_0 & = & 2ax_0 x + bx + bx_0 + 2c
\end{array}
\]
Ho ottenuto l'equazione
$$ y + y_0 = 2ax_0 x + bx + bx_0 + 2c $$
Divido per due entrambi i membri
$$ ( y + y_0 ) \cdot \frac{1}{2} = ( 2ax_0 x + bx + bx_0 + 2c ) \cdot \frac{1}{2} $$
$$ \frac{ y + y_0}{2} = \frac{2ax_0 x}{2} + \frac{bx+bx_0}{2} + \frac{2c}{2} $$
$$ \frac{y+y_0}{2} = ax_0 x + b \left( \frac{x+x_0}{2} \right) + c $$
Alla fine ottengo la formula che volevo dimostrare.
E così via.
