La sottrazione dei numeri complessi

La differenza tra due numeri complessi è un numero complesso che ha per parte reale la differenza delle parti reali e per parte immaginaria la differenza dei coefficienti delle parti immaginarie. $$ (a-bi)-(c-di) = (a-c)+(b-d)i $$

Un esempio

Prendo come esempio due numeri complessi z₁ e z₂

$$ z_1 = 5+6i $$

$$ z_2 = 2+4i $$

Calcolo la sottrazione z₁-z₂

$$ z_1 - z_2 = (5+6i)-(2+4i) $$

Sommo tra loro le parti reali e immaginarie dei due numeri complessi.

$$ z_1 - z_2 = 5+6i-2-4i) $$

$$ z_1 - z_2 = (5-2)+(6i-4i) $$

$$ z_1 - z_2 = 3+2i $$

La differenza tra i due numeri complessi z₁-z₂ è il numero complesso 3+2i.

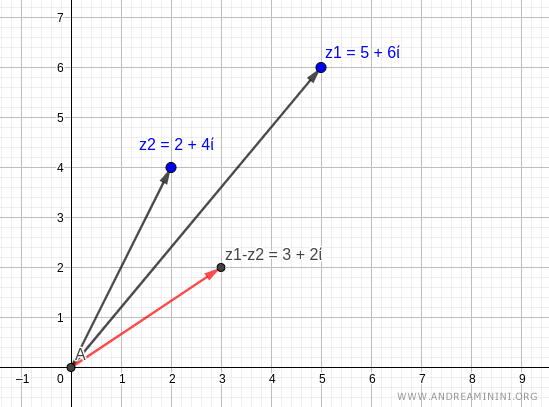
Nota. Posso calcolare la differenza anche scrivendo i due numeri complessi come coordinate del piano di Gauss (x.y) o come vettori a due dimensioni. Ad esempio, i precedenti numeri complessi z1 e z2 sul piano hanno le seguenti coppie di coordinate (o vettori) $$ z_1 = 5+6i = (5,6) $$ $$ z_2 = 2+4i = (2,4) $$ Calcolo la differenza tra i due vettori $$ z_1 – z_2 = (5,6) – (2,4) $$ $$ z_1 – z_2 = (5-2,6-4) $$ $$ z_1 – z_2 = (3,2) $$ Il risultato è sempre lo stesso.

La dimostrazione

Considero due numeri complessi z₁ e z₂

$$ z_1 = a+bi $$

$$ z_2 = c+di $$

Calcolo la differenza tra i due numeri complessi.

$$ z_1-z_2 = (a+bi)-(c+di) $$

$$ z_1-z_2 = a+bi-c-di $$

Applico la proprietà associativa e la proprietà distributiva

$$ z_1-z_2 = (a-c)+(bi-di) $$

$$ z_1-z_2 = (a-c)+i(b-d) $$

Pertanto, la differenza z₁-z₂ è un numero complesso che ha per parte reale la differenza delle parti reali (a-c) e per parte immaginaria la differenza dei coefficienti delle parti immaginarie (b-d)i.

Note a margine

Alcune osservazioni e note personali sulla sottrazione tra numeri complessi.

• La differenza tra numeri complessi coniugati
  La differenza fra due numeri complessi coniugati, \( z_1 = a + bi \) e \( z_2 = a - bi \), è un numero immaginario puro. $$ z_1 - z_2 = (a + bi) - (a - bi) = a + bi - a + bi = 2bi $$ La differenza è data solo dalla parte immaginaria, raddoppiata, con coefficiente \( 2b \). Questa proprietà si basa sull'eliminazione della parte reale e sul raddoppiamento del coefficiente della parte immaginaria, che diventa l'unico termine nella differenza.

  Esempio. Considero i numeri complessi \( z_1 = 3 + 4i \) e \( z_2 = 3 - 4i \) e calcolo la differenza $$ z_1 - z_2 = (3 + 4i) - (3 - 4i) = 3 + 4i - 3 + 4i = 8i $$ In questo caso, il risultato è un numero immaginario puro, \( 8i \), che corrisponde al doppio del coefficiente della parte immaginaria del minuendo, \( 4 \).

E così via.