Iperbole equilatera

L'iperbole equilatera è una particolare iperbole in cui l'asse trasverso e non trasverso sono di uguale lunghezza $ 2a=2b $ ovvero $ a=b $. La sua equazione standard è la seguente $$ \frac{x^2}{a^2} - \frac{y^2}{a^2} = \pm 1 $$ che si può scrivere anche in questa forma equivalente $$ x^2−y^2= \pm a^2 $$

Si tratta di una curva aperta definita come il luogo geometrico in cui tutti i punti soddisfano l'equazione x²-y²=a².

Per il resto, come nelle altre iperboli, ogni punto P della curva ha la stessa differenza di distanza dai due fuochi F₁ e F₂.

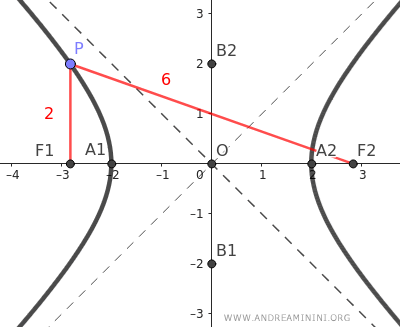
Nota. Come in qualsiasi iperbole, anche in un'iperbole equilatera la differenza delle distanze tra un punto P e i fuochi è sempre uguale a 2a. $$ | \overline{PF_1} - \overline{PF_2} | = 2a $$ Dove "a" è la distanza tra un vertice e il centro dell'iperbole. Ad esempio, se a=2 e b=2 allora la differenza delle distanze è uguale a 2a=4.

Le caratteristiche

L'iperbole equilatera si distingue dalle altre iperboli per gli assi simmetrici e uguali in lunghezza (congruenti).

Pertanto, la distanza dei vertici reali (a) e non reali (b) dal centro (O) è la stessa.

$$ a=b $$

Dove I vertici reali (a) sono i punti di intersezione dell'iperbole con l'asse trasverso. Mentre, i vertici non reali (b) sono i punti di intersezione dell'iperbole con l'asse non trasverso (o normale).

Poiché $ 2a=2b $ l'asse trasverso e non trasverso formano un quadrato anziché un rettangolo e gli asintoti coincidono con le diagonali del quadrato.

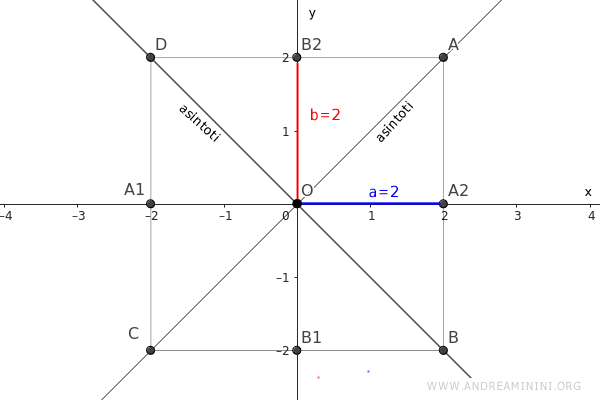
Quindi, nel caso dell'iperbole equilatera gli asintoti obliqui sono perpendicolari tra loro e coincidono con le bisettrici dei quadranti del piano cartesiano.

$$ y = x $$

$$ y = -x $$

Per il resto, i punti di fuoco si trovano sull'asse trasverso alla distanza dal centro pari a $ c=\sqrt(a^2+b^2) $ dove "a" e "b" sono le distanze dei vertici reali e non reali dal centro O dell'iperbole.

$$ c= \sqrt{a^2+b^2} $$

Nel caso in cui l'asse trasverso è l'asse x le coordinate dei fuochi sono le seguenti:

$$ F_1(-c;0) \\ F_2(c;0) $$

Se invece l'asse trasverso è l'asse y, le coordinate dei fuochi hanno queste componenti:

$$ F_1(0;-c) \\ F_2(0;c) $$

La semidistanza focale $ c $ nell'iperbole nell'iperbole si semplifica a

$$ c = \sqrt{a^2+a^2} = \sqrt{2a^2} = a \sqrt{2} $$

A sua volta l'eccentricità dell'iperbole diventa:

$$ e = \frac{c}{a} = \frac{a \sqrt{2}}{a} = \sqrt{2} $$

Infine, l'equazione canonica dell'iperbole equilatera è la seguente:

• Se i fuochi si trovano sull'asse x $$ x^2−y^2=a^2 $$
• Se i fuochi si trovano sull'asse y $$ x^2−y^2=-a^2 $$

Tutti i punti dell'iperbole equilatera devono soddisfare la precedente relazione.

Un esempio pratico

Considero una iperbole equilatera con centro sull'origine degli assi cartesiani O(0;0)

$$ x^2-y^2= 4 $$

In questo caso a²=4

$$ a^2 = 4 $$

Calcolo la radice quadrata in entrambi i membri e ottengo a=2.

$$ \sqrt{a^2} = \sqrt{4} $$

$$ a=2 $$

Ho così trovato la distanza dei vertici reali dell'iperbole dal centro sull'asse trasverso A₁A₂.

$$ A_1(-a;0) = (-2;0) $$

$$ A_2(a;0) = (2;0) $$

Rappresento i due vertici reali sul piano

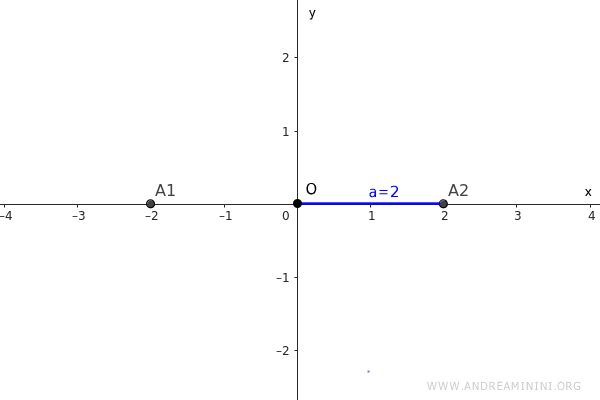
Sapendo che l'iperbole è equilatera, le variabili a=b hanno lo stesso valore, quindi anche b=2.

Pertanto, le coordinate dei vertici sull'asse non trasverso sono i seguenti:

$$ B_1(-b;0) = (-2;0) $$

$$ B_2(b;0) = (2;0) $$

Rappresento anche i vertici non reali sul piano

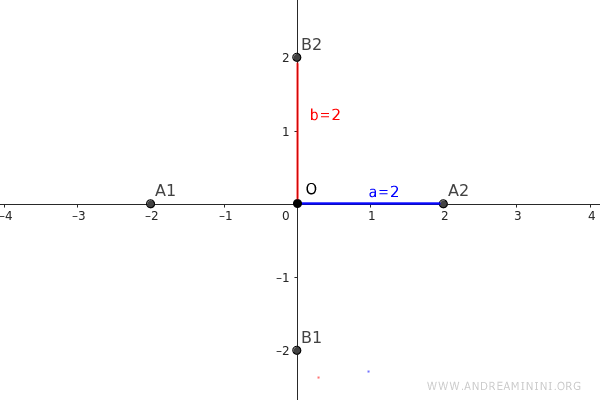
A questo punto per trovare le diagonali mi basta costruire un quadrato centrato sull'origine con lati lunghi 2a.

Le diagonali del quadrato si trovano sugli asintoti dell'iperbole equilatera.

Una volta noti "a" e "b", posso calcolare "c" ossia la distanza dei fuochi dal centro usando il teorema di Pitagora.

$$ c = \sqrt{a^2+b^2} $$

$$ c = \sqrt{2^2+2^2} = \sqrt{4+4} = \sqrt{8} = 2 \sqrt{2} = 2.83 $$

Quindi, le coordinate dei fuochi si trovano alle seguenti coordinate

$$ F_1(-c;0) = (-2.83;0) $$

$$ F_2(c;0) = (2.83;0) $$

Rappresento le coordinate dei fuochi sul piano

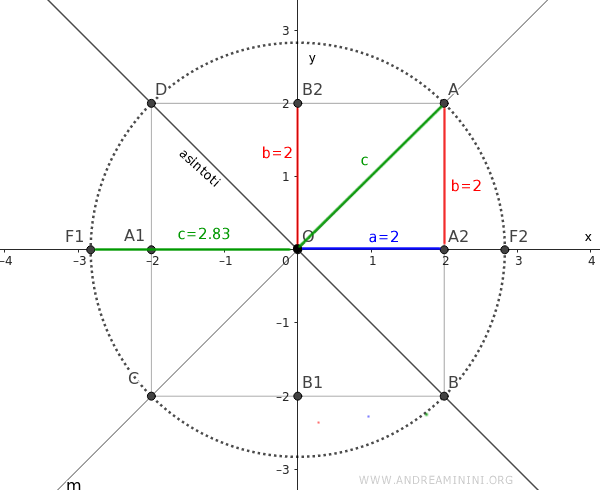
A questo punto posso calcolare i vari punti dell'iperbole usando l'equazione canonica

$$ x^2−y^2=a^2 $$

In questo caso a=2

$$ x^2−y^2=2^2 $$

$$ x^2−y^2=4 $$

Ricavo la y in funzione della x

$$ y^2 = x^2-4 $$

$$ \sqrt{y^2} = \sqrt{x^2-4} $$

$$ y = \pm \sqrt{x^2-4} $$

A questo punto calcolo le coordinate (x;y) dei punti dell'iperbole per alcuni valori della x nell'intervallo (-∞,-2.81]∪[2.81,∞).

x	y
-5	±4.58
-4	±3.46
-3	±2.24
3	±2.24
4	±3.46
5	±4.58

In questo modo posso aggiungere i primi punti dell'iperbole nel grafico.

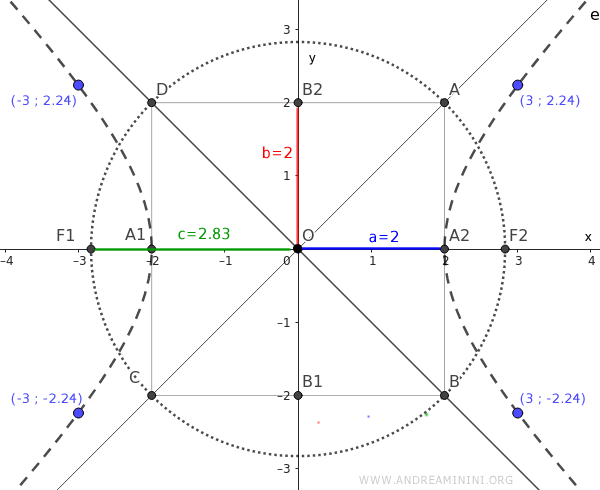
Per ultimare la costruzione della curva non devo far altro che trovare altri punti e unirli tra loro.

Il risultato finale è l'iperbole equilatera.

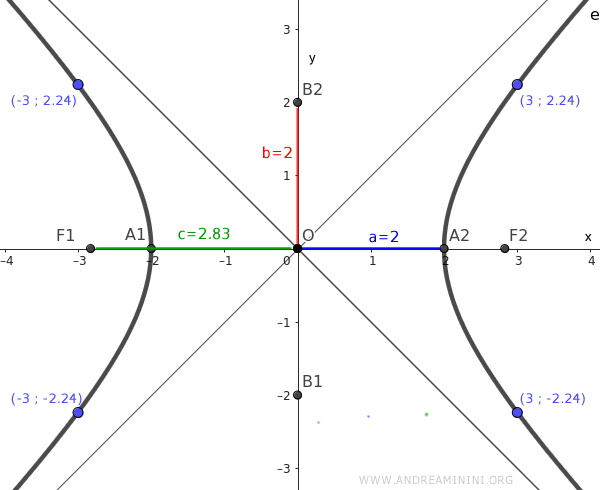
Nota. Come in qualsiasi altra iperbole, se prendo un punto P qualsiasi della curva, la differenza assoluta tra le distanze dai fuochi è costante ed è pari a 2a=4.

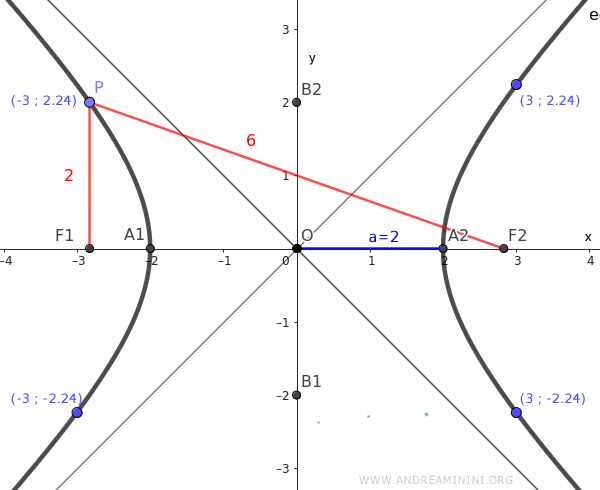
La dimostrazione

Considero una iperbole centrata sull'origine O(0;0) con gli assi trasversi sull'asse x e non trasversi sull'asse y che sono tra loro congruenti, ossia di uguale lunghezza.

$$ a=b $$

Essendo uguali, il rettangolo ABCD che ha lati di lunghezza 2a e 2b costruito al centro dell'iperbole diventa un quadrato.

 

In questo caso le diagonali del quadrato coincidono con le bisettrici dei quadranti del piano cartesiano.

$$ y = x $$

$$ y = -x $$

L'equazione canonica di un'iperbole centrata sull'origine e con i fuochi sull'asse x è la seguente:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

Sapendo che a=b, posso sostituire b² con a²

$$ \frac{x^2}{a^2} - \frac{y^2}{a^2} = 1 $$

$$ \frac{x^2-y^2}{a^2} = 1 $$

Per la proprietà invariantiva delle equazioni, moltiplico entrambi i membri dell'equazione per a²

$$ \frac{x^2-y^2}{a^2} \cdot a^2 = 1 \cdot a^2 $$

$$ x^2-y^2 = a^2 $$

Il risultato finale è l'equazione canonica dell'iperbole equilatera.

L'iperbole equilatera con gli asintoti paralleli agli assi cartesiani

L'equazione di un'iperbole equilatera con gli asintoti coincidenti con gli assi cartesiani è $$ xy=1 $$ Se gli asintoti sono paralleli agli assi cartesiani è $$ (x-x_0) \cdot (y-y_0) $$ dove $ x_0 $ e $ y_0 $ sono gli assi dell'iperbole.

L'iperbole equilatera con l'asse trasverso sulla bisettrice del piano cartesiano rappresenta una rotazione dell'iperbole equilatera standard di 45 gradi.

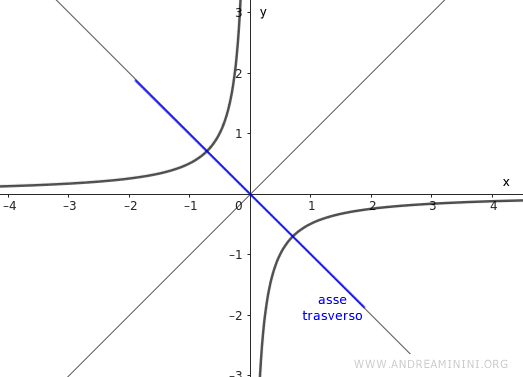
Si tratta di un caso particolare di iperbole equilatera in cui l'asse trasverso coincide con la bisettrice dei quadranti del piano anziché con gli assi.

In altre parole, le bisettrici diventano gli assi dell'iperbole mentre gli assi del piano cartesiano diventano gli asintoti dell'iperbole equilatera.

In questo sistema l'equazione dell'iperbole equilatera è la seguente:

$$ x \cdot y = k $$

Dove k è una costante positiva o negativa.

• Se k>0 i rami dell'iperbole sono nel primo e terzo quadrante.
• Se k<0 i rami dell'iperbole sono nel secondo e quarto quadrante.

Gli assi di simmetria sono le bisettrici dei quadranti

$$ y = x $$

$$ y = -x $$

La relazione tra $ k $ e la lunghezza del semiasse trasverso è

$$ k = \pm \frac{a^2}{2} $$

Pertanto, la lunghezza del semiasse trasverso è

$$ a = \overline{OA_1} = \overline{OA_2} = \sqrt{|k|+|k|} = \sqrt{2|k|} $$

I vertici reali si trovano alle coordinate

• Per k>0 $$ A_1(- \sqrt{k}; - \sqrt{k} ) $$ $$ A_2(\sqrt{k}; \sqrt{k} ) $$
• Per k<0 $$ A_1(- \sqrt{-k}; \sqrt{-k} ) $$ $$ A_2(\sqrt{-k}; -\sqrt{-k} ) $$

La semidistanza focale è

$$ c = a \sqrt{2} = \sqrt{2|k|} \cdot \sqrt{2} = 2 \sqrt{|k|} $$

Le coordinate dei fuochi sono:

• Per k>0 $$ F_1( - \sqrt{2k}; - \sqrt{2k} ) $$ $$ F_2( \sqrt{2k}; \sqrt{2k} ) $$
• Per k<0 $$ F_1( - \sqrt{-2k}; \sqrt{-2k} ) $$ $$ F_2( \sqrt{-2k}; - \sqrt{-2k} ) $$

Riepilogando, se k>0 l'asse trasverso è la bisettrice che passa per il I e il III quadrante del piano cartesiano

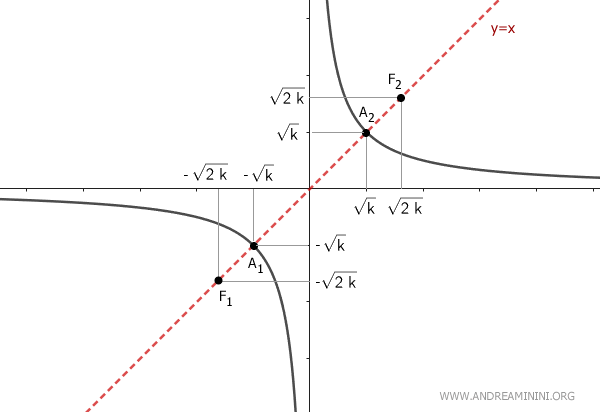
Se k<0 l'asse trasverso è la bisettrice del II e del IV quadrante del piano cartesiano.

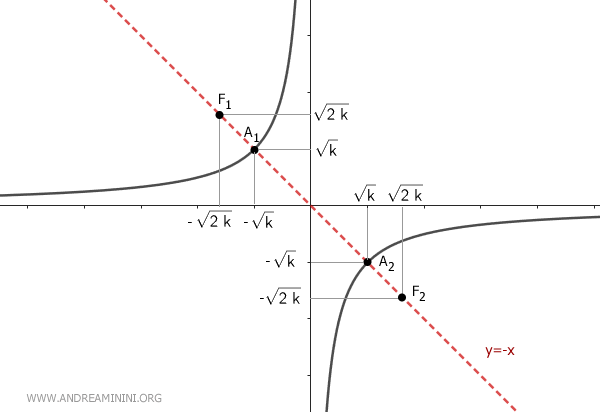
Dimostrazione

Per dimostrare le formule considero due sistemi di riferimento (x;y) e (x';y')

Il primo (x;y) si basa sugli assi cartesiani mentre il secondo (x';y') utilizza le bisettrici dei quadranti.

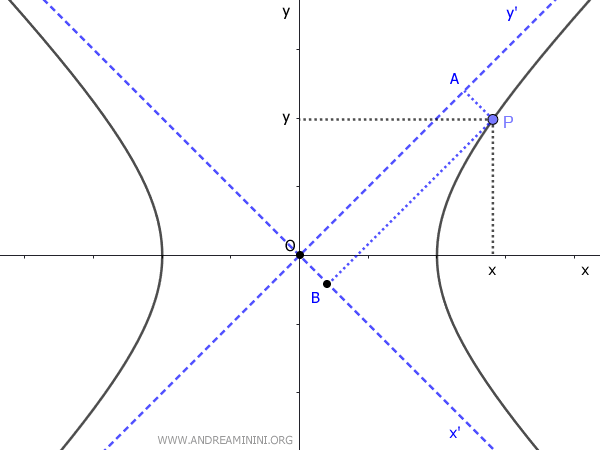
Ad esempio, il punto P nel primo sistema di riferimento si trova alle coordinate (x,y) mentre nel secondo sistema di riferimento si trova alle coordinate (x';y')

Quindi, nel secondo sistema di riferimento la lunghezza dei segmenti AP e BP è

$$ \overline{AP} = | x' | $$

$$ \overline{BP} = | y' | $$

Il prodotto di queste due lunghezze è semplicemente x'y'

$$ \overline{AP} \cdot \overline{BP}  = |x'| \cdot |y'| = |x'y'| $$

Per misurare gli stessi segmenti AP e BP nel primo sistema di riferimento (x;y) devo misurare la distanza del punto P dalle rette y' e x'.

Dove y' è la retta y=x ovvero x-y=0 mentre x' è la retta y=-x ovvero x+y=0.

La distanza di un punto P(x₀;y₀) da una retta ax+by+c=0 si misura tramite la formula:

$$ d = \frac{|ax_0+by_0+c|}{ \sqrt{a^2+b^2} } $$

La distanza AP del punto P dalla retta y' ossia  x-y=0 dove a=1 e b=-1 è la seguente:

$$ \overline{AP} = \frac{|x-y|}{ \sqrt{1^2+(-1)^2} } = \frac{|x-y|}{\sqrt{2}} $$

La distanza BP del punto P dalla retta x' ossia  x+y=0 dove a=1 e b=1 è la seguente:

$$ \overline{BP} = \frac{|x+y|}{ \sqrt{1^2+1^2} } = \frac{|x+y|}{\sqrt{2}} $$

Il prodotto di queste due lunghezze è:

$$ \overline{AP} \cdot \overline{BP}  = \frac{|x-y|}{\sqrt{2}}  \cdot  \frac{|x+y|}{\sqrt{2}} $$

$$ \overline{AP} \cdot \overline{BP}  = \frac{|x^2+xy-xy-y^2|}{\sqrt{2} \cdot \sqrt{2}}  $$

$$ \overline{AP} \cdot \overline{BP}  = \frac{|x^2-y^2|}{2}  $$

Dove nel caso di un'iperbole equilatera $ x^2 - y^2 = a^2 $

$$ \overline{AP} \cdot \overline{BP}  = \frac{a^2}{2}  $$

Riepilogando nei due sistemi di riferimento il prodotto AP·BP è

$$ \overline{AP} \cdot \overline{BP}  = |x'y'| = \frac{a^2}{2}  $$

ossia

$$ |x'y'| = \frac{a^2}{2}  $$

$$ x'y' = \pm \frac{a^2}{2}  $$

Sapendo che $ k = \frac{a^2}{2}  $ è un valore costante, lo indico con la lettera $ k $

$$ x'y' = \pm k $$

Pertanto, nel sistema di riferimento (x';y') fra le variabili x' e y' c'è un rapporto di proporzionalità inversa.

Un esempio pratico

Considero l'iperbole seguente

$$ xy = - \frac{1}{2} $$

In questo caso la costante è k=-1/2 ed è un valore negativo.

Quindi l'iperbole si trova nel secondo e nel quarto quadrante del piano cartesiano.

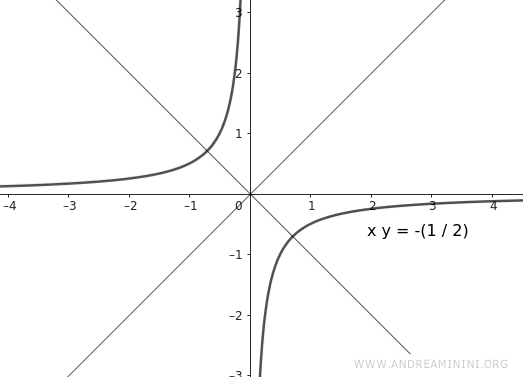
Gli assi x e y del piano sono gli asintoti dell'iperbole.

Viceversa le bisettrici del piano sono rispettiivamente l'asse trasverso e non trasverso dell'iperbole.

In questo caso $ k<1 $ e l'asse trasverso è $ y = - x $

I vertici si trovano alle coordinate:

$$ A_1(- \sqrt{-k}; \sqrt{-k} )  = (- \sqrt{- ( - \frac{1}{2} ) }; \sqrt{-( - \frac{1}{2} )} ) = \left(- \sqrt{ \frac{1}{2} } ; \sqrt{ \frac{1}{2} } \right) $$

$$ A_2(\sqrt{-k}; -\sqrt{-k} ) = (\sqrt{-( - \frac{1}{2} )}; -\sqrt{-( - \frac{1}{2} )} ) = \left( \sqrt{ \frac{1}{2} } ; - \sqrt{ \frac{1}{2} } \right) $$

La lunghezza del semiasse trasverso $ a $ è 1

$$ a = \sqrt{2|k|} = \sqrt{2 \cdot  |-\frac{1}{2} |} = 1 $$

I fuochi si trovano alle coordinate F₁(-1;1) e F₂(1;-1)

$$ F_1( - \sqrt{-2k}; \sqrt{-2k} ) = \left(  - \sqrt{-2 \cdot (- \frac{1}{2}) }; \sqrt{-2 \cdot (- \frac{1}{2}) }   \right) = \left(-1;1  \right)  $$

$$ F_2( \sqrt{-2k}; - \sqrt{-2k} ) = \left(   \sqrt{-2 \cdot (- \frac{1}{2}) }; - \sqrt{-2 \cdot (- \frac{1}{2}) }   \right)  = \left(1;-1  \right)  $$

Ecco la rappresentazione grafica:

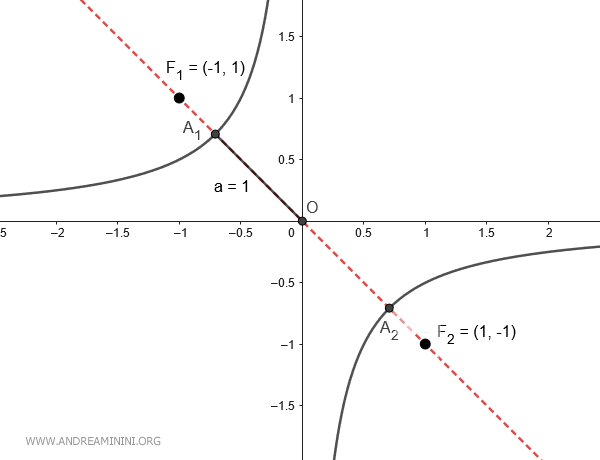
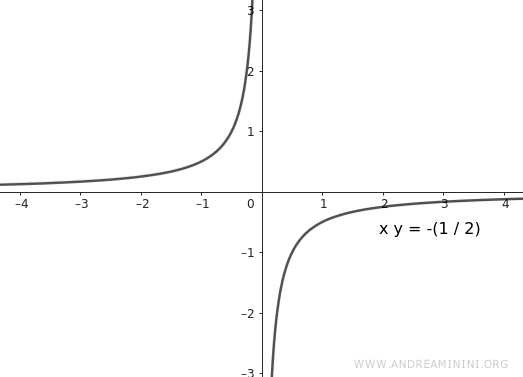
Dimostrazione. Considero un'iperbole equilatera con l'asse trasverso sull'asse x, la cui equazione canonica è $$ x^2-y^2=1 $$ Ruoto di 45° l'iperbole calcolando le nuove coordinate x' e y' tramite la matrice di riotazione. $$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \frac{\sqrt{2}}{2} & - \frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} $$ Le nuove coordinate sono le seguenti $$ x'= x \cdot \frac{\sqrt{2}}{2} - y \cdot \frac{\sqrt{2}}{2} $$ $$ y' = x \cdot \frac{\sqrt{2}}{2} + y \cdot \frac{\sqrt{2}}{2} $$ Ora sostituisco queste nuove coordinate nell'equazione canonica dell'iperbole equilatera $$ x'^2-y'^2=1 $$ $$ (x \cdot \frac{\sqrt{2}}{2} - y \cdot \frac{\sqrt{2}}{2})^2-(x \cdot \frac{\sqrt{2}}{2} + y \cdot \frac{\sqrt{2}}{2})^2=1 $$ $$ ( x \cdot \frac{\sqrt{2}}{2} )^2 - 2 xy \frac{\sqrt{2}}{2} \frac{\sqrt{2}}{2} + ( y \cdot \frac{\sqrt{2}}{2} )^2 - [ ( x \cdot \frac{\sqrt{2}}{2} )^2 + 2 xy \frac{\sqrt{2}}{2} \frac{\sqrt{2}}{2} + ( y \cdot \frac{\sqrt{2}}{2} )^2 ] = 1 $$ $$ \frac{1}{2}x^2 - xy + \frac{1}{2}y^2 - [ \frac{1}{2}x^2+xy + \frac{1}{2} y^2 ] = 1 $$ $$ -xy - xy = 1 $$ $$ -2xy = 1 $$ $$ 2xy = -1 $$ $$ xy = - \frac{1}{2} $$ In questo caso la costante è k=-1/2. Essendo k un valore negativo, l'iperbole equilatera si trova nel secondo e nel quarto quadrante.

Note

Alcune osservazioni e note a margine sulle iperboli equilatere

• L'equazione di una iperbole equilatera con gli asintoti paralleli $ (x-x_0)(y-y_0)= \pm 1 $ o coincidenti agli assi cartesiani $ xy= \pm 1 $ è un caso particolare di funzione omografica $$ y = \frac{ax+b}{cx+d} $$ con $ c \ne 0 $ e $ ad-bc \ne 0 $ e centro nel punto $ C \left( -  \frac{d}{c}; \frac{a}{c}  \right)  $ e gli asintoti in $ x = - \frac{d}{c} $ e $ y = \frac{a}{c} $

  Vale la pena notare che se $ c=0 $ o $ ad-bc=0 $ la funzione non è più un'iperbole perché degenera in una retta.
  

  Esempio. Considero l'equazione di un'iperbole equilatera centrata nell'origine con gli asintoti coincidenti con gli assi cartesiani $$ xy=1 $$ Applico una traslazione dell'iperbole dal centro $ O(0;0) $ al centro $ C(2;3) $.
  
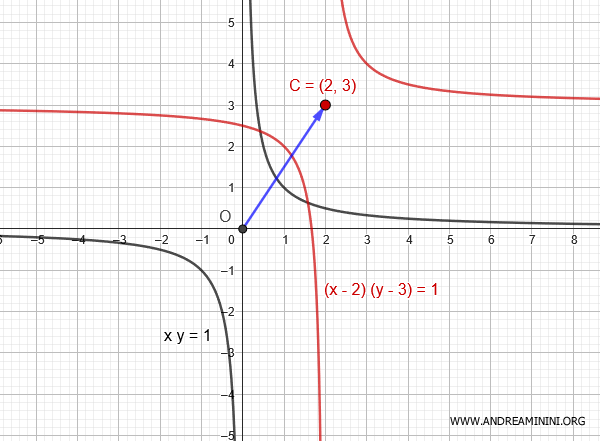
  Ogni punto dell'iperbole viene traslato nella stessa misura $$ \begin{cases} x'=x+2 \\ \\ y'=y+3 \end{cases} $$ Ricavo le variabili $ x $ e $ y $ $$ \begin{cases} x=x'-2 \\ \\ y=y'-3 \end{cases} $$ Quindi, sostituisco $ x=x'-2 $ e $ y = y-3 $ nell'equazione dell'iperbole $$ xy=1 $$ $$ (x'-2) \cdot (y'-3)=1 $$ Elimino gli apici per semplicità. $$ (x-2) \cdot (y-3)=1 $$ Quest'ultima è l'equazione dell'iperbole equilatera centrata nel punto $ C(2;3) $ con gli asintoti paralleli agli assi cartesiani in $ x_0 =2 $ e $ y_0=3 $. Ricavo la variabile y $$ (x-2) \cdot (y-3)=1 $$ $$ xy-3x-2y+6=1 $$ $$ y(x-2)=1-6+3x $$ $$ y=\frac{ 3x-5 }{x-2} $$ Questo conferma che l'iperbole equilatera con gli asintoti coincidenti o paralleli agli assi cartesiani è una funzione omografica $ y = \frac{ax+b}{cx+d} $ dove $ a= 3 $, $ b=-5 $, $c=1$, $ d=-2 $. La condizione $ c \ne 0 $ e $ ad-bc \ne 0 $ è soddisfatta. Quindi, è un'iperbole con centro in $ C(2;3) $ e gli asintoti in $$ x = - \frac{d}{c} = - \frac{-2}{1} = 2 $$ $$ y = \frac{a}{c} = \frac{3}{1} = 3  $$

E così via.