L'equazione dell'iperbole date le coordinate di un punto e di un fuoco

Per determinare l'equazione di un'iperbole centrata nell'origine, dato un punto \( P(x_0, y_0) \) e uno dei suoi fuochi \( F(c, 0) \), posso seguire due metodi alternativi:

• Metto a sistema la relazione $ c^2 = a^2 + b^2 $ e l'equazione dell'iperbole sostituendo $ x $ e $ y $ con le coordinate del punto \( P(x_0, y_0) \) $$ \begin{cases} \frac{x_0^2}{a^2} - \frac{y_0^2}{b^2} = 1 \\ \\ c^2 = a^2 + b^2 \end{cases} $$
• Calcolo la distanza tra il punto P e i fuochi sapendo che $ | PF - PF' | = 2a $ e una volta trovata la distanza $ a $ di un vertice dal centro, calcolo anche la distanza $ b $ dell'altro vertice tramite la relazione $ c^2 = a^2 + b^2 $

Nota. Se il fuoco si trova sull'asse x l'equazione dell'iperbole è $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ Viceversa, se il fuoco si trova sull'asse y l'equazione da considerare è $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$

Metodo 1

Supponiamo di avere un'iperbole centrata nell'origine degli assi che passa per il punto \( P(3, 4) \) e ha il fuoco alle coordinate \( F(5, 0) \).

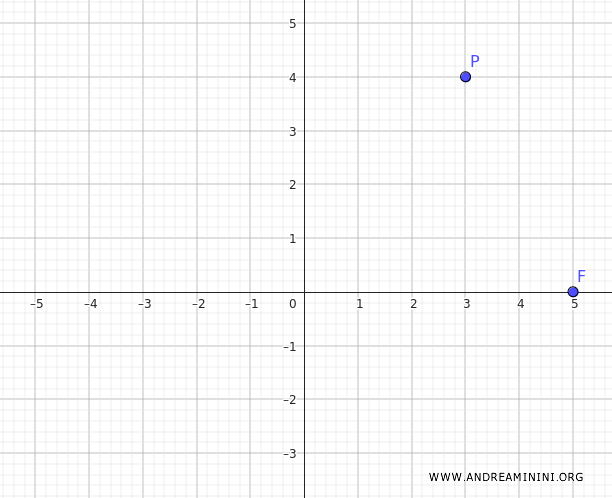
Il fuoco si trova sull'asse x, quindi l'equazione canonica dell'iperbole si scrive in questa forma:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

Costruisco un sistema di equazioni con l'equazione canonica dell'iperbole e la relazione $ c^2 = a^2+b^2 $

$$ \begin{cases} \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \\ \\ c^2 = a^2 + b^2 \end{cases} $$

Sostituisco x e y con le coordinate del punto $ P(3,4) $ ossia $ x = 3 $ e $ y = 4 $

$$ \begin{cases} \frac{3^2}{a^2} - \frac{4^2}{b^2} = 1 \\ \\ c^2 = a^2 + b^2 \end{cases} $$

$$ \begin{cases} \frac{9}{a^2} - \frac{16}{b^2} = 1 \\ \\ c^2 = a^2 + b^2 \end{cases} $$

Poiché conosco le coordinate del fuoco $ F(c,0)=(5,0) $, so già che la distanza del fuoco dal centro dell'iperbole è $ c=5 $

$$ \begin{cases} \frac{9}{a^2} - \frac{16}{b^2} = 1 \\ \\ 5^2 = a^2 + b^2 \end{cases} $$

$$ \begin{cases} \frac{9}{a^2} - \frac{16}{b^2} = 1 \\ \\ 25 = a^2 + b^2 \end{cases} $$

A questo punto risolvo il sistema utilizzando il metodo della sostituzione.

$$ \begin{cases} \frac{9}{(25 - b^2 )} - \frac{16}{b^2} = 1 \\ \\ a^2 = 25 - b^2  \end{cases} $$

$$ \begin{cases} \frac{9b^2 - 16(25 - b^2 )}{b^2(25 - b^2 )}= 1 \\ \\ a^2 = 25 - b^2  \end{cases} $$

$$ \begin{cases} 9b^2 - 16(25 - b^2 )= b^2(25 - b^2 ) \\ \\ a^2 = 25 - b^2  \end{cases} $$

$$ \begin{cases} 9b^2 - 400 + 16b^2= 25b^2 - b^4 \\ \\ a^2 = 25 - b^2  \end{cases} $$

$$ \begin{cases} 9^2 - 400 + 16b^2- 25b^2 + b^4 = 0 \\ \\ a^2 = 25 - b^2  \end{cases} $$

$$ \begin{cases} b^4 - 400 = 0 \\ \\ a^2 = 25 - b^2  \end{cases} $$

$$ \begin{cases} \sqrt{b^4} = \sqrt{400} \\ \\ a^2 = 25 - b^2  \end{cases} $$

$$ \begin{cases} b^2 = 20 \\ \\ a^2 = 25 - b^2  \end{cases} $$

Nota. La radice quadrata di 400 è $ \sqrt{400} = \pm 20 $ ma poiché $ b $ è una lunghezza, scarto il valore negativo (-20) e prendo in considerazione solo il valore positivo (+20)-

Una volta trovato $ b^2 = 20 $ lo sostituisco nella seconda equazione per trovare anche la distanza dell'altro vertice dal centro $ a $

$$ \begin{cases} b^2 = 20 \\ \\ a^2 = 25 - 20  \end{cases} $$

$$ \begin{cases} b^2 = 20 \\ \\ a^2 = 5  \end{cases} $$

A questo punto posso scrivere l'equazione canonica dell'iperbole sostituendo $ a^2=5 $ e $ b^2 = 20 $

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{5} - \frac{y^2}{20} = 1 $$

Questa è l'equazione dell'iperbole che passa per il punto $ P(4,5) $ e ha un fuoco alle coordinate $ F(5,0) $

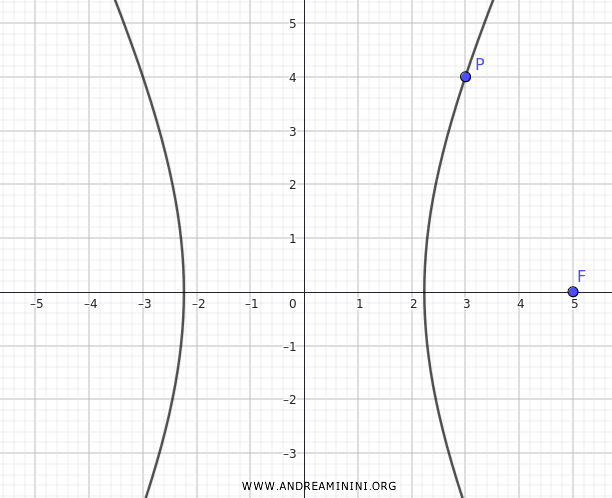
Metodo 2

Considero la stessa iperbole centrata nell'origine degli assi che passa per il punto \( P(3, 4) \) e ha il fuoco alle coordinate \( F(5, 0) \).

Dalle coordinate del fuoco $ F(c,0)=(5,0) $ deduco che la distanza del fuoco dal centro è $ c = 5 $

Inoltre, poiché il fuoco si trova sull'asse x, l'equazione canonica dell'iperbole è la seguente:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

Determino la distanza tra il fuoco $ F $ e il punto $ P $

$$ \overline{PF} = \sqrt{(x_0 - c)^2 + (y_0-0)^2} $$

Dove $ c=5 $ e le coordinate del punto sono $ x_0=3 $ e $ y_0=4 $

$$ \overline{PF} = \sqrt{(3- 5)^2 + 4^2} $$

$$ \overline{PF} = \sqrt{4 + 16} $$

$$ \overline{PF} = \sqrt{20} $$

$$ \overline{PF} = \sqrt{2^2 \cdot 5} $$

$$ \overline{PF} = 2 \sqrt{ 5} $$

Se un fuoco è \( F(5, 0) \), l'altro fuoco sarà \( F'(-5, 0) \).

Calcola la distanza tra il punto $ P $ e l'altro fuoco $ F' $

$$ PF' = \sqrt{(3 - (-5))^2 + (4-0)^2} $$

$$ PF' = \sqrt{8^2 + 4^2} $$

$$ PF' = \sqrt{64 + 16} $$

$$ PF' = \sqrt{80} $$

$$ PF' = \sqrt{2^4 \cdot 5} $$

$$ PF' = 2^2 \sqrt{5} $$

$$ PF' = 4 \sqrt{5} $$

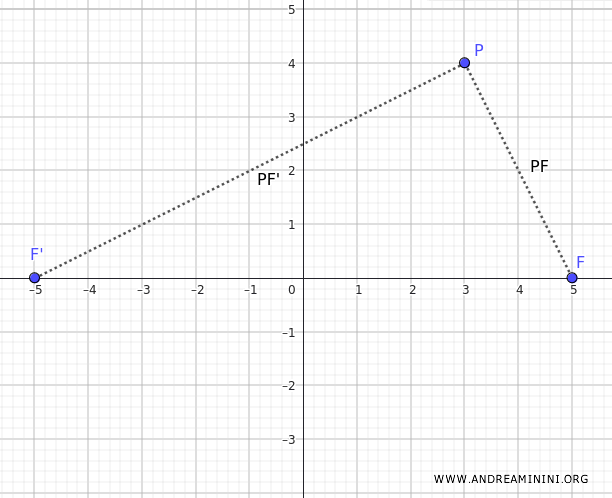
L'iperbole è il luogo dei punti tali che la differenza delle distanze dai due fuochi è costante e uguale a \( 2a \), dove \( 2a \) è la distanza tra i due vertici dell'iperbole. Quindi:

$$ | PF - PF' | = 2a $$

Sapendo che $ \overline{PF} = 2 \sqrt{5} $ e $ PF' = 4 \sqrt{5} $

$$ | 2 \sqrt{5} - 4\sqrt{5} | = 2a $$

$$ | - 2\sqrt{5} | = 2a $$

$$ 2\sqrt{5}  = 2a $$

$$ a = \sqrt{5}  $$

Dove \( a \) è la semi-distanza tra i vertici dell'iperbole.

In un'iperbole la relazione tra \( a \), \( b \) (semi-asse trasverso) e \( c \) (distanza focale) è data da:

$$ c^2 = a^2 + b^2 $$

Sostituisco $ c=5 $ e $ a = \sqrt{5}  $

$$ 5^2 = (\sqrt{5})^2 + b^2 $$

$$ 25 = 5 + b^2 $$

$$ b^2 = 25 - 5 $$

$$ b^2 = 20 $$

$$ b = \sqrt{20} $$

Una volta noto $ a = \sqrt{5}  $ e $ b = \sqrt{20} $ li sostituisco nell'equazione canonica dell'iperbole.

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{(\sqrt{5})^2} - \frac{y^2}{(\sqrt{20})^2} = 1 $$

$$ \frac{x^2}{5} - \frac{y^2}{20} = 1 $$

Questa è l'equazione dell'iperbole che passa per il punto \( (3, 4) \) e ha uno dei suoi fuochi in \( (5, 0) \).

E così via.