Equazione dell'iperbole che passa per due punti
Per scrivere l'equazione di un'iperbole centrata nell'origine che passa per due punti noti $ P_1(x_1;y_1) $ e $ P_2(x_2;y_2) $, seguo questi passi:
In base ai dati del problema devo capire qual'è l'asse trasverso, quello con i fuochi:
- Se l'asse trasverso è l'asse x, l'equazione canonica dell'iperbole è $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
- Se l'asse trasverso è l'asse y, l'equazione canonica dell'iperbole è $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
Quando non è possibile capire qual'è l'asse trasverso, devo considerare entrambe le ipotesi.
Poi costruisco un sistema di equazioni con due equazioni canoniche dell'iperbole, sostituendo le coordinate x e y rispettivamente con quelle dei punti noti $ P_1(x_1;y_1) $ e $ P_2(x_2;y_2) $.
Un esempio pratico
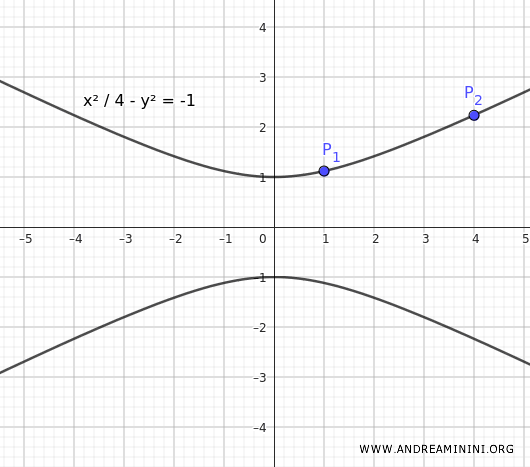
Considero un'equazione dell'iperbole con i fuochi sull'asse y che passa per i punti $ P_1(1; \frac{\sqrt{5}}{2}) $ e $ P_2(4;\sqrt{5}) $
Poiché i fuochi sono sull'asse y, l'equazione canonica dell'iperbole è la seguente:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
Costruisco un sistema di equazioni con due equazioni dell'iperbole, sostituendo le coordinate x e y con quelle dei due punti noti $ P_1(1; \frac{\sqrt{5}}{2}) $ e $ P_2(4;\sqrt{5}) $.
$$ \begin{cases} \frac{x_1^2}{a^2} - \frac{y_1^2}{b^2} = -1 \\ \\ \frac{x_2^2}{a^2} - \frac{y_2^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{1^2}{a^2} - \frac{(\frac{\sqrt{5}}{2})^2}{b^2} = -1 \\ \\ \frac{4^2}{a^2} - \frac{(\sqrt{5})^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{1}{a^2} - \frac{\frac{5}{4}}{b^2} = -1 \\ \\ \frac{16}{a^2} - \frac{5}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{1}{a^2} - \frac{5}{4} \cdot \frac{1}{b^2} = -1 \\ \\ \frac{16b^2-5a^2}{a^2b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{1}{a^2} - \frac{5}{4b^2} = -1 \\ \\ \frac{16b^2-5a^2}{a^2b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{4b^2-5a^2}{4a^2b^2} = -1 \\ \\ 16b^2-5a^2 = -a^2b^2 \end{cases} $$
$$ \begin{cases} 4b^2-5a^2 = -4a^2b^2 \\ \\ 16b^2-5a^2 = -a^2b^2 \end{cases} $$
Ora risolvo il sistema, ricavo la $ b $ nella prima equazione e la sostituisco nella seconda equazione.
$$ \begin{cases} 4b^2 + 4a^2b^2 = 5a^2 \\ \\ 16b^2-5a^2 = -a^2b^2 \end{cases} $$
$$ \begin{cases} b^2 \cdot (4 + 4a^2) = 5a^2 \\ \\ 16b^2-5a^2 = -a^2b^2 \end{cases} $$
$$ \begin{cases} b^2 = \frac{5a^2}{4 + 4a^2} \\ \\ 16b^2-5a^2 = -a^2b^2 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ 16b^2-5a^2 = -a^2b^2 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ 16( \sqrt{ \frac{5a^2}{4 + 4a^2} } )^2-5a^2 = -a^2( \sqrt{ \frac{5a^2}{4 + 4a^2} } )^2 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ 16 \cdot \frac{5a^2}{4 + 4a^2} -5a^2 = -a^2 \cdot \frac{5a^2}{4 + 4a^2} \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ \frac{80a^2 - 5a^2 \cdot (4 + 4a^2)}{4 + 4a^2} = -\frac{5a^4}{4 + 4a^2} \end{cases} $$
Moltiplico entrambi i lati della seconda equazione per $ 4+4a^2 $ e semplifico
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ 80a^2 - 5a^2 \cdot (4 + 4a^2) = -5a^4 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ 80a^2 - 20a^2 - 20a^4 + 5a^4 = 0 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ -15a^4 + 60a^2 = 0 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ a^2(60-15a^2) = 0 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ 3a^2(20-5a^2) = 0 \end{cases} $$
La seconda equazione ha due radici $ a=0 $ e $ a = \sqrt{\frac{20}{5}} = \sqrt{4} = 2 $$
Essendo una lunghezza, ignoro il valore nullo e considero soltanto la radice positiva $ a=2 $
Una volta nota la lunghezza del semiasse non trasverso $ a=2 $ lo sostituisco nella prima equazione per trovare il valore corrispondente di $ b $
$$ \begin{cases} b = \sqrt{ \frac{5 \cdot 2^2}{4 + 4 \cdot 2^2} } \\ \\ a = 2 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5 \cdot 4}{4 + 4 \cdot 4} } \\ \\ a = 2 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{20}{4 + 16} } \\ \\ a = 2 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{20}{20} } \\ \\ a = 2 \end{cases} $$
$$ \begin{cases} b = \sqrt{ 1 } \\ \\ a = 2 \end{cases} $$
$$ \begin{cases} b = 1 \\ \\ a = 2 \end{cases} $$
Pertanto, i semiassi dell'iperbole sono $ a =2 $ e $ b = 1 $
Li sostituisco nell'equazione canonica dell'iperbole
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
$$ \frac{x^2}{2^2} - \frac{y^2}{1^2} = -1 $$
$$ \frac{x^2}{4} - y^2 = -1 $$
Questa è l'equazione dell'iperbole con i fuochi sull'asse y che passa per i punti $ P_1(1; \frac{\sqrt{5}}{2}) $ e $ P_2(4;\sqrt{5}) $
E così via.
