Equazione dell'iperbole noto un asintoto e un fuoco

Per determinare l'equazione di un'iperbole centrata nell'origine, la conoscenza di un fuoco mi permette subito di capire se l'asse trasverso è l'asse x o l'asse y.

• Se il fuoco è $F(c;0)$ allora l'asse trasverso è l'asse x e l'equazione dell'iperbole è $$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$
• Se il fuoco è $F(0;c)$ allora l'asse trasverso è l'asse y e l'equazione dell'iperbole è $$\frac{x^2}{a^2} - \frac{y^2}{b^2} = -1$$

In entrambi i casi le equazioni degli asintoti dell'iperbole sono:

$$y = \pm \frac{b}{a}$$

La relazione tra i semiassi $a$ e $b$ e la distanza $c$ del fuoco dal centro dell'iperbole è sempre la seguente:

$$c^2 = a^2 + b^2$$

Dati questi elementi, posso risalire all'equazione dell'iperbole.

Un esempio pratico

Considero un'iperbole che ha un fuoco alle coordinate

$$F(c;0) = F(5;0)$$

e un asintoto

$$y = \sqrt{\frac{2}{3}} x$$

Il fuoco si trova sull'asse x, quindi l'equazione dell'iperbole si scrive in questo modo:

$$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$

Per trovare i semiassi $a$ e $b$, costruisco un sistema con l'equazione dell'asintoto e la relazione tra i semiassi dell'iperbole.

$$\begin{cases} y = \pm \frac{b}{a} x \\ \\ c^2 = a^2 + b^2 \end{cases}$$

Conosco già l'equazione di un asintoto $y = \sqrt{\frac{2}{3}} x$ e la distanza del fuoco dal centro ossia $c=5$

$$\begin{cases} \sqrt{\frac{2}{3}} x = \frac{b}{a} x \\ \\ 5^2 = a^2 + b^2 \end{cases}$$

Divido entrambi i lati della prima equazione per $x$

$$\begin{cases} \sqrt{\frac{2}{3}} = \frac{b}{a} \\ \\ 25 = a^2 + b^2 \end{cases}$$

Ricavo $b$ nella prima equazione

$$\begin{cases} b = \sqrt{\frac{2}{3}} a \\ \\ 25 = a^2 + b^2 \end{cases}$$

Sostituisco $b$ nella seconda equazione

$$\begin{cases} b = \sqrt{\frac{2}{3}} a \\ \\ 25 = a^2 + (\sqrt{\frac{2}{3}} a)^2 \end{cases}$$

$$\begin{cases} b = \sqrt{\frac{2}{3}} a \\ \\ 25 = a^2 + \frac{2}{3} a^2 \end{cases}$$

$$\begin{cases} b = \sqrt{\frac{2}{3}} a \\ \\ 25 = \frac{3a^2+2a^2}{3} \end{cases}$$

$$\begin{cases} b = \sqrt{\frac{2}{3}} a \\ \\ 25 = \frac{5a^2}{3} \end{cases}$$

$$\begin{cases} b = \sqrt{\frac{2}{3}} a \\ \\ a^2 = 25 \cdot \frac{3}{5} \end{cases}$$

$$\begin{cases} b = \sqrt{\frac{2}{3}} a \\ \\ a^2 = 15 \end{cases}$$

$$\begin{cases} b = \sqrt{\frac{2}{3}} a \\ \\ \sqrt{a^2} = \sqrt{15} \end{cases}$$

$$\begin{cases} b = \sqrt{\frac{2}{3}} a \\ \\ a = \sqrt{15} \end{cases}$$

Una volta noto $a = \sqrt{15}$ lo sostituisco nella prima equazione per trovare $b$

$$\begin{cases} b = \sqrt{\frac{2}{3}} \sqrt{15} \\ \\ a = \sqrt{15} \end{cases}$$

$$\begin{cases} b = \sqrt{\frac{2}{3} \cdot 15}  \\ \\ a = \sqrt{15} \end{cases}$$

$$\begin{cases} b = \sqrt{10}  \\ \\ a = \sqrt{15} \end{cases}$$

Quindi, la lunghezza dei semiassi dell'iperbole è $a = \sqrt{15}$ e $b = \sqrt{10}$ che posso sostituire nell'equazione canonica dell'iperbole.

$$\frac{x^2}{( \sqrt{15} )^2} - \frac{y^2}{( \sqrt{10} )^2} = 1$$

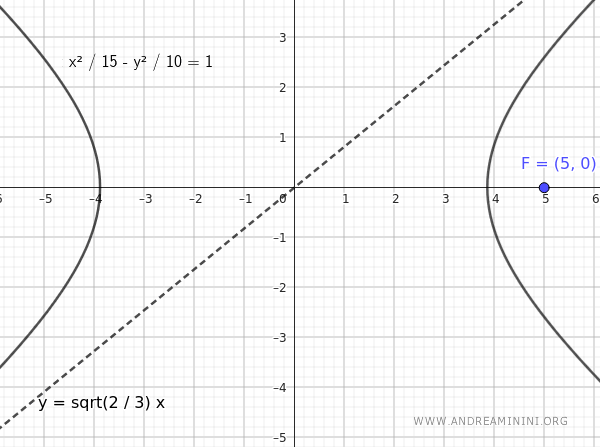
$$\frac{x^2}{15} - \frac{y^2}{10} = 1$$

Questa è l'equazione dell'iperbole che ha un fuoco alle coordinate $F(c;0) = F(5;0)$ e un asintoto $y = \sqrt{\frac{2}{3}} x$.

E così via.