Equazione dell'iperbole noto un asintoto e un punto
Per determinare l'equazione di una iperbole centrata nell'origine conoscendo l'equazione dell'asintoto $ y = \frac{b}{a} x $ e le coordinate $ P(x_0;y_0) $ di un punto dell'iperbole, seguo questi passaggi.
In base ai dati del problema cerco di capire qual'è l'asse trasverso, quello dove si trovano i fuochi, per determinare l'equazione canonica dell'iperbole
- Se l'asse trasverso è l'asse x l'equazione dell'iperbole è $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
- Se l'asse trasverso è l'asse y l'equazione dell'iperbole è $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
Costruisco un sistema con l'equazione canonica e l'equazione dell'iperbole.
$$ \begin{cases} y = \pm \frac{b}{a} x \\ \\ \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 \end{cases} $$
Nell'equazione canonica dell'iperbole sostituisco $ x $ e $ y $ con le coordinate del punto noto $ P(x_0;y_0) $
$$ \begin{cases} y = \pm \frac{b}{a} x \\ \\ \frac{x_0^2}{a^2} - \frac{y_0^2}{b^2} = \pm 1 \end{cases} $$
Risolvendo il sistema risalgo alla lunghezza dei semiassi $ a $ e $ b $, necessari per scrivere l'equazione dell'iperbole.
Un esempio pratico
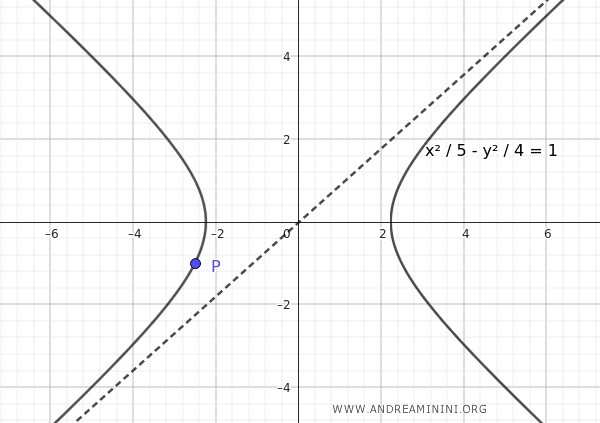
Devo trovare l'equazione dell'iperbole centrata nell'origine degli assi con i fuochi sull'asse x che passa per il punto $ P( - \frac{5}{2};-1) $ e l'equazione di un asintoto è $ y= \frac{2}{\sqrt{5}} x $$
Poiché i fuochi si trovano sull'asse x, l'equazione canonica dell'iperbole è:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
Sostituisco $ x $ e $ y $ con le coordinate del punto noto $ P( - \frac{5}{2};-1) $
$$ \frac{(- \frac{5}{2})^2}{a^2} - \frac{(-1)^2}{b^2} = 1 $$
$$ \frac{\frac{25}{4}}{a^2} - \frac{1}{b^2} = 1 $$
$$ \frac{25}{4} \cdot \frac{1}{a^2} - \frac{1}{b^2} = 1 $$
$$ \frac{25}{4a^2} - \frac{1}{b^2} = 1 $$
Costruisco un sistema di equazioni con l'asintoto e l'equazione dell'iperbole con le coordinate del punto noto
$$ \begin{cases} y= \frac{2}{\sqrt{5}} x \\ \\ \frac{25}{4a^2} - \frac{1}{b^2} = 1 \end{cases} $$
Sapendo che l'equazione dell'iperbole è $ y = \frac{b}{a} x $
$$ \begin{cases} \frac{b}{a} x= \frac{2}{\sqrt{5}} x \\ \\ \frac{25}{4a^2} - \frac{1}{b^2} = 1 \end{cases} $$
$$ \begin{cases} \frac{b}{a} = \frac{2}{\sqrt{5}} \\ \\ \frac{25}{4a^2} - \frac{1}{b^2} = 1 \end{cases} $$
$$ \begin{cases} b = \frac{2}{\sqrt{5}} a \\ \\ \frac{25}{4a^2} - \frac{1}{b^2} = 1 \end{cases} $$
Sostituisco $ b = \frac{2}{\sqrt{5}} a $ nella seconda equazione
$$ \begin{cases} b = \frac{2}{\sqrt{5}} a \\ \\ \frac{25}{4a^2} - \frac{1}{(\frac{2}{\sqrt{5}} a)^2} = 1 \end{cases} $$
$$ \begin{cases} b = \frac{2}{\sqrt{5}} a \\ \\ \frac{25}{4a^2} - \frac{1}{ \frac{4a^2}{5} } = 1 \end{cases} $$
$$ \begin{cases} b = \frac{2}{\sqrt{5}} a \\ \\ \frac{25}{4a^2} - \frac{5}{4a^2} = 1 \end{cases} $$
$$ \begin{cases} b = \frac{2}{\sqrt{5}} a \\ \\ \frac{25-5}{4a^2} = 1 \end{cases} $$
$$ \begin{cases} b = \frac{2}{\sqrt{5}} a \\ \\ \frac{20}{4a^2} = 1 \end{cases} $$
$$ \begin{cases} b = \frac{2}{\sqrt{5}} a \\ \\ \frac{5}{a^2} = 1 \end{cases} $$
$$ \begin{cases} b = \frac{2}{\sqrt{5}} a \\ \\ a^2 = 5 \end{cases} $$
$$ \begin{cases} b = \frac{2}{\sqrt{5}} a \\ \\ \sqrt{a^2} = \sqrt{5} \end{cases} $$
$$ \begin{cases} b = \frac{2}{\sqrt{5}} a \\ \\ a = \sqrt{5} \end{cases} $$
Una volta trovato il semiasse $ a= \sqrt{5} $ lo sostituisco nella prima equazione per trovare anche $ b $
$$ \begin{cases} b = \frac{2}{\sqrt{5}} \cdot \sqrt{5} \\ \\ a = \sqrt{5} \end{cases} $$
$$ \begin{cases} b = 2 \\ \\ a = \sqrt{5} \end{cases} $$
Quindi, noti i semiassi $ a = \sqrt{5} $ e $ b=2 $ posso completare l'equazione canonica dell'iperbole.
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{(\sqrt{5})^2} - \frac{y^2}{2^2} = 1 $$
$$ \frac{x^2}{5} - \frac{y^2}{4} = 1 $$
Questa è l'equazione dell'iperbole centrata nell'origine degli assi con i fuochi sull'asse x che passa per il punto $ P( - \frac{5}{2};-1) $ e l'equazione di un asintoto è $ y= \frac{2}{\sqrt{5}} x $
E così via.
