Equazione dell'iperbole dato un vertice e una tangente
Per determinare l'equazione di un'iperbole centrata nell'origine degli assi dati una retta tangente e un vertice, seguo questi passaggi.
- Cerco di capire dai dati del problema qual'è l'asse trasverso, quello con i fuochi. Se l'asse trasverso è l'asse x l'equazione dell'iperbole è $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ Se l'asse trasverso è l'asse y l'equazione dell'iperbole è $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
- Costruisco un sistema con l'equazione canonica dell'iperbole e l'equazione della tangente.$$ \begin{cases} \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 \\ \\ a'x+b'y +c'=0 \end{cases} $$
- Sostituisco il dato sul vertice noto e risolvo il sistema per cercare il vertice mancante, tenendo conto che la condizione di tangenza si verifica quando il discriminante è nullo. $ \Delta = 0 $
Un esempio pratico
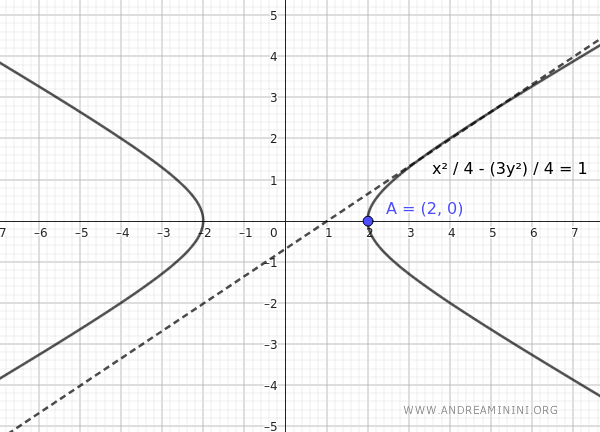
Un'iperbole centrata nell'origine è tangente alla retta $ 2x-3y-2=0 $ e ha un vertice reale in $ A(2;0) $.
Sapendo che un vertice reale si trova in $ A(2;0) $ deduco che $ a=2 $ e l'asse trasverso si trova sull'asse x, quindi l'equazione della iperbole è:
$$ \frac{x^2}{a^2} - {y^2}{b^2} = 1 $$
$$ \frac{x^2}{2^2} - {y^2}{b^2} = 1 $$
$$ \frac{x^2}{4} - {y^2}{b^2} = 1 $$
Costruisco un sistema di equazioni con l'equazione dell'iperbole e della retta per trovare il punto di tangenza.
$$ \begin{cases} 2x-3y - 2 = 0 \\ \\ \frac{x^2}{4} - {y^2}{b^2} = 1 \end{cases} $$
Per verificare la tangenza, dobbiamo sostituire l'equazione della retta nell'equazione dell'iperbole e verificare se ottengo una sola soluzione, cioè la retta tocca l'iperbole in un solo punto.
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ \frac{x^2}{4} - {y^2}{b^2} = 1 \end{cases} $$
Ora sostituisco la \(y\) nell'equazione dell'iperbole:
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ \frac{x^2}{4} - \frac{\left( \frac{2x-2}{3} \right)^2}{b^2} = 1 \end{cases} $$
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ \frac{x^2}{4} - \frac{ \frac{4x^2 -8x +4 }{9} }{b^2} = 1 \end{cases} $$
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ \frac{x^2}{4} - \frac{4x^2 -8x +4 }{9} \cdot \frac{1}{b^2} = 1 \end{cases} $$
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ \frac{x^2}{4} - \frac{4x^2 -8x +4 }{9b^2} = 1 \end{cases} $$
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ \frac{9b^2x^2 + 4 \cdot (-4x^2 +8x -4= }{4 \cdot 9b^2} = 1 \end{cases} $$
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ \frac{9b^2x^2 -16x^2 +32x -16 }{36b^2} = 1 \end{cases} $$
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ 9b^2x^2 -16x^2 +32x -16 = 36b^2 \end{cases} $$
Riorganizzo i termini
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ (9b^2 -16) \cdot x^2 +32x -16 - 36b^2 = 0 \end{cases} $$
Perché la retta sia tangente all'iperbole, questa equazione quadratica deve avere una sola soluzione, il che significa che il discriminante deve essere uguale a zero.
Dove il discriminante di un'equazione quadratica \(Ax^2 + Bx + C = 0\) è dato da \(B^2 - 4AC\).
$$ \Delta = B^2 - 4AC = 0 $$
In questo caso $ A =9b^2 -16, \quad B = 32, \quad C = -16 - 36b^2 $
$$ 32^2 - 4 \cdot (9b^2 -16 ) \cdot ( -16 - 36b^2 ) = 0 $$
$$ 1024 - 4 \cdot (9b^2 -16 ) \cdot ( -16 - 36b^2 ) = 0 $$
Divido entrambi i lati dell'equazione per 4
$$ \frac{1}{4} \cdot [ 1024 - 4 \cdot (9b^2 -16 ) \cdot ( -16 - 36b^2 ) ] = \frac{1}{4} \cdot 0 $$
$$ 256 - (9b^2 -16 ) \cdot ( -16 - 36b^2 ) = 0 $$
$$ 256 - 9b^2 \cdot ( -16 - 36b^2 ) + 16 \cdot ( -16 - 36b^2 ) = 0 $$
$$ 256 + 144b^2 + 324 b^4 - 256 - 576b^2 = 0 $$
$$ 324 b^4 - 432b^2 = 0 $$
$$ b^2 ( 324 b^2 - 432 ) = 0 $$
Quindi il determinante $ \Delta = 0 $ si annulla quando $ b^2 = 0 $ oppure $ b^2 = \frac{432}{324} = \frac{4}{3} $
Ignoro $ b^2 = 0 $ perché il semiasse dell'iperbole non può essere nullo, quindi $ b^2 = \frac{4}{3} $
$$ b^2 = \frac{4}{3} $$
$$ \sqrt{b^2} = \sqrt{ \frac{4}{3} } $$
$$ b = 2 \sqrt{ \frac{1}{3} } $$
Una volta note le lunghezze dei semiassi $ a = 2 $ e $ b = 2 \sqrt{ \frac{1}{3} } $, le sostituisco nell'equazione canonica dell'iperbole.
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{2^2} - \frac{y^2}{( 2 \sqrt{ \frac{1}{3} } )^2} = 1 $$
$$ \frac{x^2}{4} - \frac{y^2}{ \frac{4}{3} } = 1 $$
$$ \frac{x^2}{4} - y^2 \cdot \frac{3}{4}= 1 $$
$$ \frac{x^2}{4} - \frac{3y^2}{4}= 1 $$
Moltiplico entrambi i lato dell'equazione per 4.
$$ 4 \cdot ( \frac{x^2}{4} - \frac{3y^2}{4} )= 1 \cdot 4 $$
$$ x^2 - 3y^2 = 4 $$
Questa è l'equazione dell'iperbole centrata nell'origine che è tangente alla retta $ 2x-3y-2=0 $ e ha un vertice reale in $ A(2;0) $.
E così via.
