L'equazione dell'iperbole noto un punto e un vertice
Quando conosco le coordinate di un punto $ P(x_0;y_0) e di un vertice A o B di un'iperbole centrata nell'origine, posso completare l'equazione seguendo questi passaggi:
Poiché non conosco le coordinate dei fuochi, non so stabilire se l'asse maggiore dell'iperbole è orizzontale o verticale, quindi devo considerare entrambe le ipotesi
$$ \frac{x^2}{a^2} + \frac{x^2}{b^2} = \pm 1 $$
Sostituisco le coordinate del punto noto e del vertice nell'equazione.
Quindi, risolvo l'equazione per determinare l'altro vertice.
Esempio
In questo esercizio devo trovare l'equazione di un'iperbole centrata nell'origine degli assi cartesiani che ha un vertice reale in $ A( \sqrt{5};0 ) $ e passa per il punto $ P(- \frac{5}{2};1) $
Il vertice reale si trova sull'asse x, quindi l'asse maggiore dove si trovano i fuochi dell'iperbole è orizontale.
Pertanto, l'equazione dell'iperbole è la seguente:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
La scrivo in una forma più comoda per i calcoli che seguono
$$ \frac{b^2x^2-a^2y^2}{a^2b^2} = 1 $$
$$ b^2x^2-a^2y^2 = a^2b^2 $$
Sostituisco le coordinate del punto noto $ P(- \frac{5}{2};1) $ nell'equazione dell'iperbole, ossia $ x= - \frac{5}{2} $ e $ y=1 $.
$$ b^2 \cdot (- \frac{5}{2})^2-a^ \cdot(1)^2 = a^2b^2 $$
$$ \frac{25}{4} b^2 -a^2 = a^2b^2 $$
$$ \frac{25}{4}b^2 -a^2 = a^2b^2 $$
Ora sostituisco le coordinate del vertice noto $ A(a;0)=( \sqrt{5};0 ) $ ossia $ a=\sqrt{5} $
$$ \frac{25}{4}b^2 -( \sqrt{5} )^2 = ( \sqrt{5} )^2b^2 $$
$$ \frac{25}{4}b^2 - 5 = 5b^2 $$
$$ \frac{25}{4}b^2 - 5b^2 = 5 $$
$$ \frac{25b^2-20b^2}{4} = 5 $$
$$ \frac{5b^2}{4} = 5 $$
$$ b^2 = 5 \cdot \frac{4}{5} $$
$$ b^2 = 4 $$
Pertanto, se $ b^2 = 4 $ il semiasse non reale è lungo $ b=2 $
A questo punto, sostituisco $ a= \sqrt{5} $ e $ b=2 $ nell'equazione canonica dell'iperbole.
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{(\sqrt{5})^2} - \frac{y^2}{2^2} = 1 $$
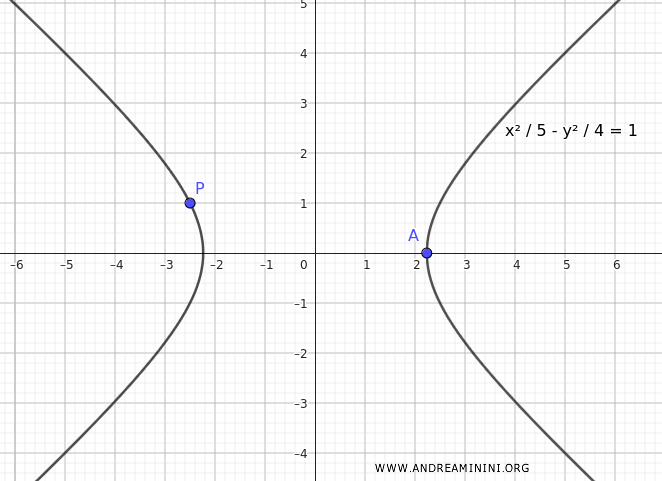
$$ \frac{x^2}{5} - \frac{y^2}{4} = 1 $$
Quest'ultima è l'equazione dell'iperbole centrata nell'origine che ha un vertice reale in $ A( \sqrt{5};0 ) $ e passa per il punto $ P(- \frac{5}{2};1) $
E così via.
