Retta secante, tangente o esterna a una iperbole
Una retta $$ a'x+b'y+c=0 $$ e una iperbole $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 $$ possono essere secanti, tangenti o esterne
- Se hanno due punti in comune sono secanti.
- Se hanno un punto in comune possono essere tangenti oppure la retta è parallela a un asintoto.
- Se non hanno punti in comune sono esterne.
Quindi, la presenza di un solo punto in comune non implica necessariamente la condizione di tangenza.
Per stabilire la posizione della retta rispetto all'iperbole, devo costruire un sistema di equazioni
$$ \begin{cases} \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 \\ \\ a'x+b'y+c=0 \end{cases} $$
Poi studiare l'equazione risolvente.
- Se l'equazione risolvente è di secondo grado (2°)
- $ \Delta>0 $
se il discriminante è maggiore di zero, esistono due soluzioni reali e la retta è secante all'iperbole in due punti distinti.
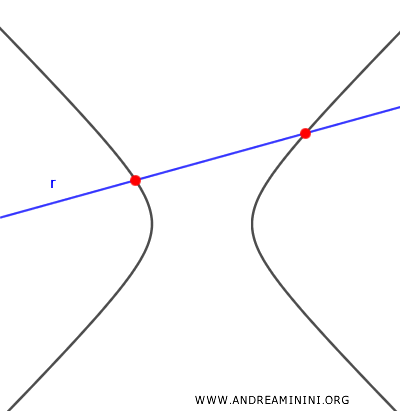
- $ \Delta=0 $
se il discriminante è nullo, esiste una sola soluzione reale e la retta è tangente all'iperbole.
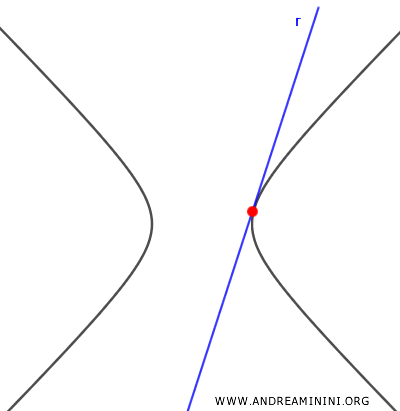
- $ \Delta<0 $
se il discriminante è negativo, non ci sono soluzioni reali e la retta è esterna all'iperbole.
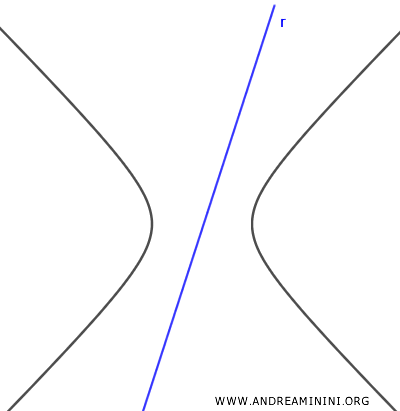
- $ \Delta>0 $
- Se l'equazione risolvente è di primo grado (1°), ossia lineare, allora la retta è secante all'iperbole in un punto.
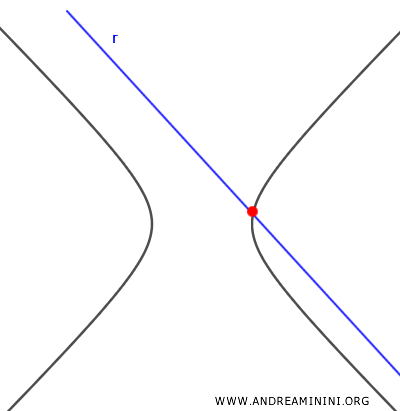
Un esempio pratico
Considero un'iperbole
$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$
e una retta
$$ x+y-1=0 $$
Devo capire se sono tangenti, secanti o esterne.
Costruisco il sistema di equazioni.
$$ \begin{cases} \frac{x^2}{4} - \frac{y^2}{3} = 1 \\ \\ x+y-1=0 \end{cases} $$
Ricavo le y in entrambe le equazioni
$$ \begin{cases} y^2 = 3 \cdot ( \frac{x^2}{4} - 1 ) \\ \\ y=1-x \end{cases} $$
$$ \begin{cases} y = \sqrt{ \frac{3x^2}{4} - 3 } \\ \\ y=1-x \end{cases} $$
Poi eguaglio le equazioni y=y e ottengo l'equazione risolvente del sistema.
$$ \sqrt{ \frac{3x^2}{4} - 3 } = 1 - x $$
$$ ( \sqrt{ \frac{3x^2}{4} - 3 } )^2 = ( 1 - x )^2 $$
$$ \frac{3x^2}{4} - 3 = 1 -2x+x^2 $$
$$ \frac{3x^2}{4} - 3 - 1 +2x-x^2 = 0 $$
$$ \frac{3x^2-4x^2}{4} +2x - 4 = 0 $$
$$ -\frac{x^2}{4} +2x -4= 0 $$
L'equazione risolvente è un'equazione di 2° grado, quindi la retta non è parallela a un asintoto dell'iperbole.
Calcolo il discriminante dell'equazione di 2° grado.
$$ \Delta = b^2 - 4ac $$
Dove $ a = - \frac{1}{4} $, $ b=2 $, $ c=-4 $
$$ \Delta = 2^2 - 4 \cdot ( - \frac{1}{4} ) \cdot (-4) $$
$$ \Delta = 4 - 4 $$
$$ \Delta = 0 $$
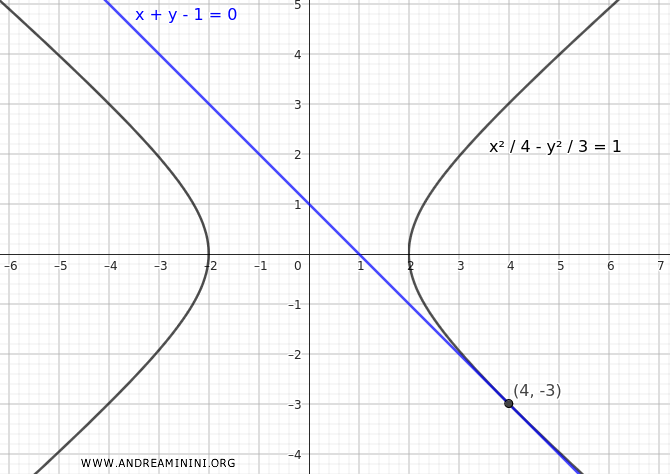
Il discriminante è nullo, quindi la retta è tangente all'iperbole.
Calcolo il valore dell'ascissa $ x $ del punto di tangenza.
$$ x = \frac{-b \pm \Delta}{2a} $$
$$ x = \frac{-2 \pm 0}{2 \cdot (- \frac{1}{4} )} $$
$$ x = \frac{-2}{- \frac{1}{2}} $$
$$ x = \frac{2}{ \frac{1}{2}} $$
$$ x = 2 \cdot \frac{2}{1} $$
$$ x = 4 $$
Una volta trovata la componente $ x=4 $ del punto di tangenza, la sostituisco nell'equazione della retta per ottenere la componente y
$$ y=1-x $$
$$ y=1-4 $$
$$ y=-3 $$
Quindi, il punto di tangenza si trova alle coordinate $ (x;y)=(4;-3) $
Esempio 2
Considero un'iperbole
$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$
e una retta
$$ y = - \frac{ \sqrt{3} }{2} x+\frac{1}{2} $$
Devo capire se la retta è secante, tangente o esterna.
Nota. Osservando il coefficiente angolare della retta $ - \frac{ \sqrt{3} }{2} $ mi posso già accorgere che la retta è parallela a un asintoto dell'iperbole. Gli asintoti dell'iperbole sono ottenuti dall'equazione $$ y = \pm \frac{b}{a}x $$ In questo caso $ a^2=4 $ e $ b^2 = 3 $ , quindi $ a= 2 $ e $ b= \sqrt{3} $. $$ y = \pm \frac{\sqrt{3}}{2}x $$ Quindi, il coefficiente angolare della retta coincide con quello di un asintoto. Da questo posso già dedurre che la retta è secante in un punto dell'iperbole. In ogni caso, per completezza svolgerò tutti i calcoli.
Costruisco il sistema di equazioni
$$ \begin{cases} \frac{x^2}{4} - \frac{y^2}{3} = 1 \\ \\ y = - \frac{ \sqrt{3} }{2} x+\frac{1}{2} \end{cases} $$
$$ \begin{cases} y^2 = 3 \cdot ( \frac{x^2}{4} - 1 ) \\ \\ y = - \frac{ \sqrt{3} }{2} x+\frac{1}{2} \end{cases} $$
$$ \begin{cases} y = \sqrt{ \frac{3x^2}{4} - 3 } \\ \\ y = - \frac{ \sqrt{3} }{2} x+\frac{1}{2} \end{cases} $$
Quindi, l'equazione risolvente eguagliando y=y è
$$ \sqrt{ \frac{3x^2}{4} - 3 } = - \frac{ \sqrt{3} }{2} x+\frac{1}{2} $$
$$ ( \sqrt{ \frac{3x^2}{4} - 3 } )^2 = ( - \frac{ \sqrt{3} }{2} x+\frac{1}{2} )^2 $$
$$ \frac{3x^2}{4} - 3 = (- \frac{ \sqrt{3} }{2} x )^2 + 2 \cdot (- \frac{ \sqrt{3} }{2} x ) \cdot \frac{1}{2} + ( \frac{1}{2} )^2 $$
$$ \frac{3x^2}{4} - 3 = \frac{ 3 }{4} x^2 - \frac{\sqrt{3} x}{2} + \frac{1}{4} $$
$$ \require{cancel} \cancel{ \frac{3x^2}{4} } - 3 - \cancel{ \frac{ 3 }{4} x^2 } + \frac{\sqrt{3} x}{2} - \frac{1}{4} = 0 $$
$$ \frac{\sqrt{3} x}{2} - 3 - \frac{1}{4} = 0 $$
$$ \frac{\sqrt{3} x}{2} - \frac{12}{4} - \frac{1}{4} = 0 $$
$$ \frac{\sqrt{3} x}{2} - \frac{13}{4} = 0 $$
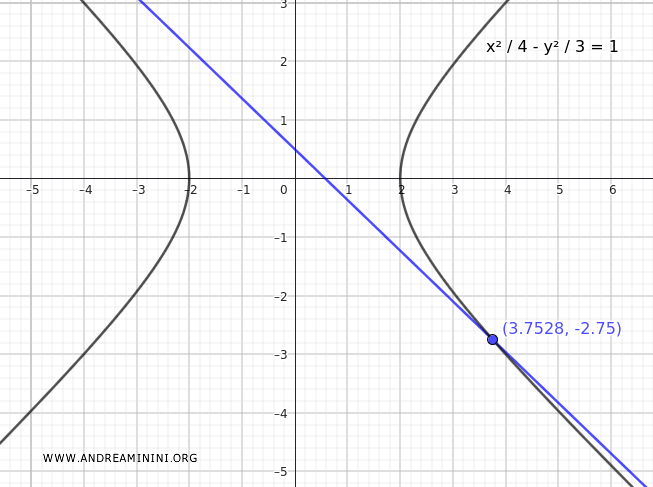
L'equazione risolvente è un'equazione lineare, quindi la retta è secante all'iperbole in un punto.
Questo vuole dire che la retta è parallela a un asintoto dell'iperbole.
A questo punto ricavo la componente x del punto in comune.
$$ x = \frac{13}{4} \cdot \frac{2}{ \sqrt{3}} $$
$$ x = \frac{13}{2 \sqrt{3} } $$
Nota. Gli asintoti dell'iperbole sono $$ y = \pm \frac{b}{a} x $$ dove $ a = 2 $ e $ b = \sqrt{3} $ $$ y = \pm \frac{\sqrt{3}}{2} x $$ Come si può subito notare, il coefficiente angolare di un asintoto è uguale al coefficiente angolare della retta $ -\frac{ \sqrt{3} }{2} $
Per trovare anche la componente y del punto secante, sostituisco $ x = \frac{13}{2 \sqrt{3} } $ nell'equazione della retta.
$$ y = - \frac{ \sqrt{3} }{2} x+\frac{1}{2} $$
$$ y = - \frac{ \sqrt{3} }{2} \cdot \frac{13}{2 \sqrt{3} } +\frac{1}{2} $$
$$ y = - \frac{13}{4} +\frac{1}{2} $$
$$ y = \frac{-13+2}{4} $$
$$ y = -\frac{11}{4} $$
Ecco il grafico della retta e dell'iperbole secanti in un punto.
E così via.
