L'equazione di una iperbole noto un vertice e un fuoco
Per trovare l'equazione di un'iperbole centrata nell'origine conoscendo le coordinate di un fuoco e di un vertice, posso seguire i seguenti passaggi.
- Se il fuoco \((c, 0)\) e il vertice \((a, 0)\) sono sull'asse \(x\), allora l'equazione è nella forma: $$
\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ Se invece il fuoco \((0, c)\) e il vertice \((0, b)\) sono sull'asse \( y \) l'equazione da considerare è $$
\frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$ - Calcolo \(b\) usando la relazione tra \(a\), \(b\) e \(c\): $$ c^2 = a^2 + b^2 $$
Una volta note le lunghezze dei vertici \(a\) e \(b\) sull'asse trasverso e non trasverso, posso scrivere l'equazione dell'iperbole.
Esempio
Considero un'iperbole centrata nell'origine degli assi cartesiani $ O(0,0) $, di cui conosco le coordinate di un fuoco in \(F(5, 0)\) e un vertice in \(A(3, 0)\).
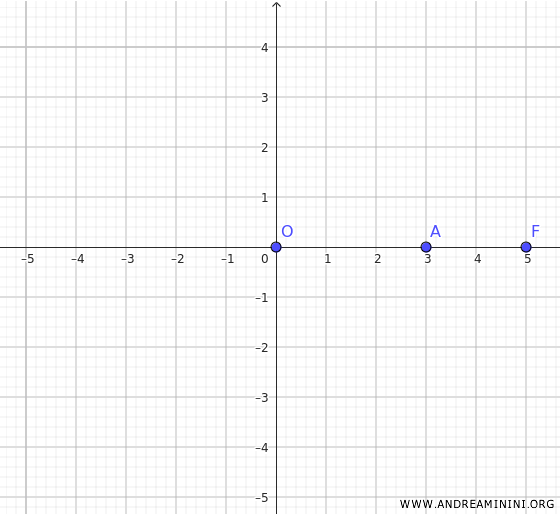
I fuochi si trovano sull'asse x, quindi l'equazione dell'iperbole che devo considerare è la seguente:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
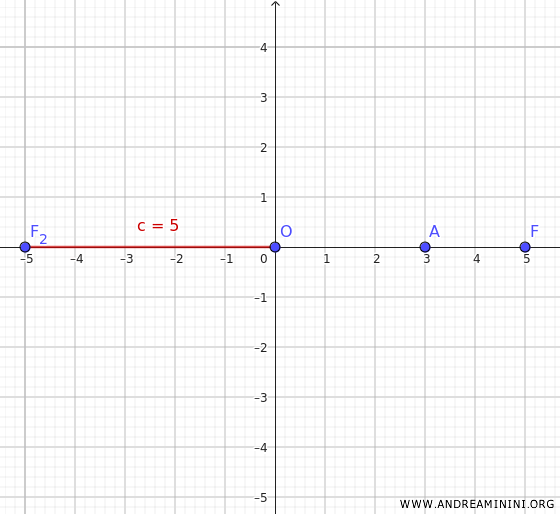
Essendo l'iperbole simmetrica rispetto al centro e agli assi, se conosco le coordinate di un fuoco \(F(5, 0)\) posso ottenere immediatamente anche le coordinate dell'altro fuoco \(F_2(-5,0) \)
In entrambi i casi la distanza del fuoco dal centro è $ c = 5 $
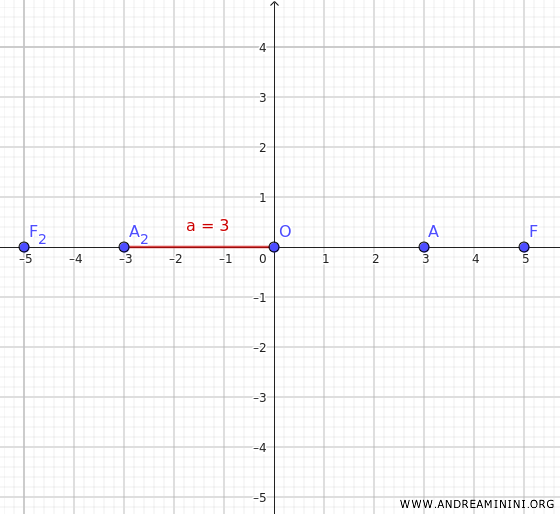
Allo stesso modo, conoscendo le coordinate di un vertice \(A(3, 0)\) ottengo quelle dell'altro vertice \(A_2(-3, 0)\)
Quindi, la distanza di ogni vertice dal centro è $ a = 3 $
A questo punto utilizzo la relazione seguente per ottenere la lunghezza dell'asse non trasverso $ b $
$$ c^2 = a^2+b^2 $$
$$ 5^2 = 3^2 + b^2 $$
$$ 25 = 9 + b^2 $$
$$ b^2 = 25-9 $$
$$ b^2 = 16 $$
$$ \sqrt{b^2} = \sqrt{16} $$
$$ b = \pm 4 $$
Essendo $ b $ una lunghezza, scarto il valore negativo.
$$ b = 4 $$
A questo punto, sapendo che $ a=3 $ , $ b = 4 $ posso scrivere l'equazione dell'iperbole:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
Sostituendo i valori di \(a\) e \(b\):
$$ \frac{x^2}{3^2} - \frac{y^2}{4^2} = 1 $$
$$ \frac{x^2}{9} - \frac{y^2}{16} = 1 $$
Quindi, l'equazione dell'iperbole centrata nell'origine con il fuoco in \((5, 0)\) e il vertice in \((3, 0)\) è $ \frac{x^2}{9} - \frac{y^2}{16} = 1 $
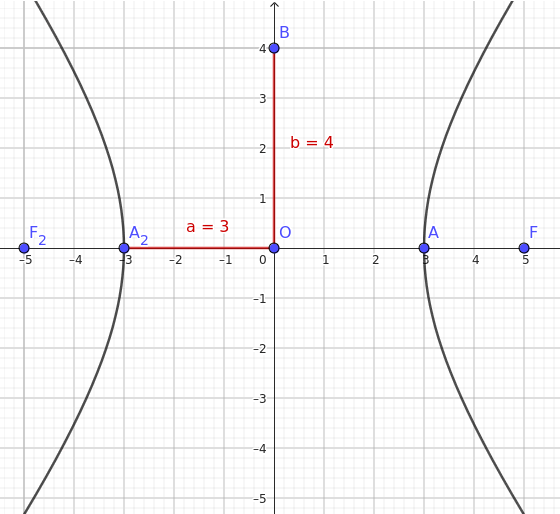
E così via.
