Equazione di una iperbole dato un fuoco e una tangente

Per determinare l'equazione di una iperbole dato un fuoco e una tangente, seguo questi passaggi:

• In base ai dati del problema cerco di capire se l'asse trasverso è l'asse x $$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$ oppure l'asse y $$\frac{x^2}{a^2} - \frac{y^2}{b^2} = -1$$ Da questo deriva l'equazione canonica dell'iperbole.
• La conoscenza del fuoco mi permette di usare la relazione $c^2 = a^2+b^2$ con $a$ e $b$ incognite
• Metto a confronto l'equazione della retta tangente e la formula di sdoppiamento $\frac{x_0x}{a^2} - \frac{y_0y}{b^2} = 1$ per ottenere le coordinate $(x_0;y_0)$ del punto di tangenza in termini di $a^2$ e $b^2$. Poi le sostituisco nell'equazione della retta tangente e ottengo un'altra equazione con $a$ e $b$ incognite.
• Costruisco un sistema con le due equazioni per trovare $a^2$ e $b^2$

Questi passaggi mi permettono di scrivere l'equazione dell'iperbole.

Esempio pratico

L'equazione di un'iperbole centrata nell'origine con un fuoco alle coordinate $F( \sqrt{7},0 )$ e una retta tangente $x-y = 1$

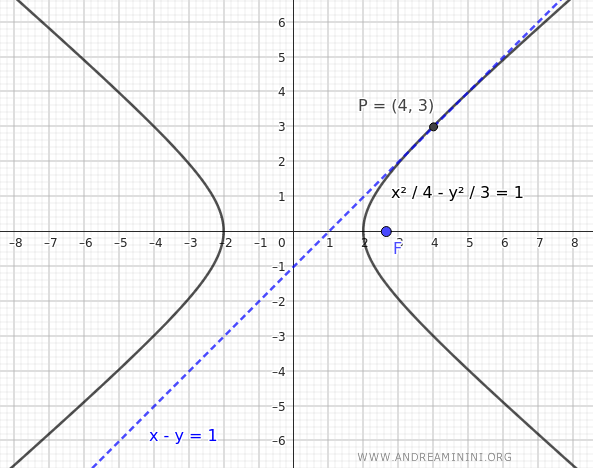
Il fuoco si trova sull'asse x, quindi l'equazione dell'iperbole è la seguente:

$$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$

Dove $a$ e $b$ sono i semiassi dell'iperbole. L'iperbole ha i fuochi lungo l'asse $x$, quindi possiamo usare la relazione tra i parametri $a$, $b$ e la distanza focale $c$, dove $c^2 = a^2 + b^2$.

Il fuoco si trova alle coordinate $F( \sqrt{7},0 )$, quindi alla distanza $c=\sqrt{7}$ dal centro dell'iperbole.

$$c = \sqrt{7}$$

Sapendo che in un'iperbole $c^2 = a^2+b^2$

$$c^2 = a^2 + b^2$$

$$(\sqrt{7} )^2 = a^2+b^2$$

$$a^2+b^2 = 7 \quad \text{(equazione 1)}$$

Ora devo trovare un'altra equazione ce abbia come incognite le variabili $a$ e $b$.

L'altro dato del problema è la retta tangente data dall'equazione $x - y = 1$.

Nel caso di una iperbole l'equazione della retta tangente in un punto $(x_0, y_0)$ dell'iperbole è data da:

$$\frac{x_0x}{a^2} - \frac{y_0y}{b^2} = 1$$

Metto a confronto questa equazione con cl'equazione della retta tangente $x - y = 1$

$$\underbrace{ \frac{x_0}{a^2} }_1 x - \underbrace{ \frac{y_0}{b^2} }_1 y= 1 \Leftrightarrow x-y=1$$

Da questo confronto deduco che i coefficienti della x e della y sono:

$$\frac{x_0}{a^2} = 1 \quad \text{e} \quad -\frac{y_0}{b^2} = -1$$

Questo implica che

$$x_0 = a^2 \quad \text{e} \quad y_0 = b^2$$

Quindi, il punto di tangenza $(x_0, y_0)$ della retta sull'iperbole è $(a^2, b^2)$.

Il punto $(x_0,y_0)=(a^2, b^2)$ è tangente, quindi appartiene sia all'iperbole che alla retta $x - y = 1$.

Pertanto , posso sostituire $x = a^2$ e $y = b^2$ nell'equazione della tangente $x - y = 1$:

$$a^2 - b^2 = 1 \quad \text{(Equazione 2)}$$

In questo modo ottengo un'altra equazione con $a$ e $b$ incognite.

Costruisco un sistema di equazioni con le equazioni trovate e risolvo il sistema.

$$\begin{cases} a^2+b^2 = 7  \\ \\ a^2 - b^2 = 1 \end{cases}$$

Ricavo $a^2$ nella prima equazione e la sostituisco nella seconda.

$$\begin{cases} a^2 = 7 - b^2  \\ \\ a^2 - b^2 = 1 \end{cases}$$

$$\begin{cases} a^2 = 7 - b^2  \\ \\ 7 - b^2  - b^2 = 1 \end{cases}$$

$$\begin{cases} a^2 = 7 - b^2  \\ \\ - 2b^2 = 1-7 \end{cases}$$

$$\begin{cases} a^2 = 7 - b^2  \\ \\ - 2b^2 = -6 \end{cases}$$

$$\begin{cases} a^2 = 7 - b^2  \\ \\ 2b^2 = 6 \end{cases}$$

$$\begin{cases} a^2 = 7 - b^2  \\ \\ b^2 = \frac{6}{2} \end{cases}$$

$$\begin{cases} a^2 = 7 - b^2  \\ \\ b^2 = 3 \end{cases}$$

Una volta ottenuto $b^2 =3$ lo sostituisco nella prima equazione per trovare anche $a^2$

$$\begin{cases} a^2 = 7 - 3  \\ \\ b^2 = 3 \end{cases}$$

$$\begin{cases} a^2 = 4  \\ \\ b^2 = 3 \end{cases}$$

Noti $a^2=4$  e $b^2 = 3$ posso sostituirli nell'equazione canonica dell'iperbole.

$$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$

$$\frac{x^2}{4} - \frac{y^2}{3} = 1$$

Questa è l'equazione dell'iperbole che ha un fuoco alle coordinate $F( \sqrt{7},0 )$ e una retta tangente $x-y = 1$

E così via.