La formula di sdoppiamento dell'iperbole
La formula di sdoppiamento mi permette di trovare la retta tangente a un punto $ P(x_0;y_0) $ dell'iperbole. $$ \frac{xx_0}{a^2} - \frac{yy_0}{b^2} = \pm 1 $$
Questa formula si ottiene sostituendo nell'equazione canonica dell'iperbole $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 $$ sostituendo $ x^2 \rightarrow xx_0 $ e $ y^2 \rightarrow yy_0 $.
Deriva dall'applicazione delle formule di sdoppiamento delle coniche al caso particolare dell'iperbole.
Nota. Ovviamente queste formule sono utili esclusivamente per ottenere l'equazione della retta tangente in un punto dell'iperbole. Non può essere utilizzata se il punto non appartiene all'iperbole.
Un esempio pratico
Considero l'equazione di un'iperbole
$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$
Voglio trovare la retta tangente al punto $ P(4;3) $ dell'iperbole.
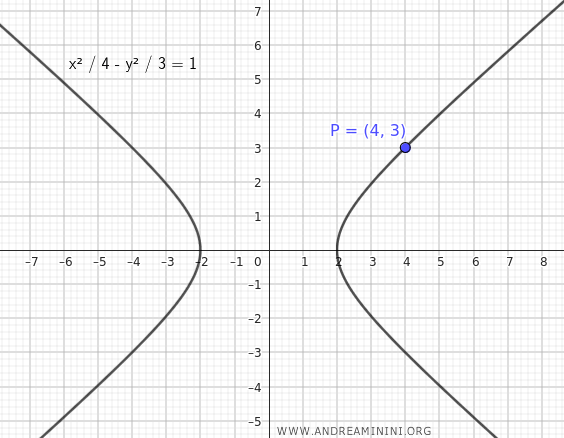
Innanzitutto, verifico se il punto $ P $ è un punto dell'iperbole, sostituendo le coordinate $ x=4 $ e $ y=3 $ nell'equazione dell'iperbole.
$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$
$$ \frac{4^2}{4} - \frac{3^2}{3} = 1 $$
$$ 4 - 3 = 1 $$
$$ 1 = 1 $$
L'equazione è soddisfatta, questo significa che il punto $ P(4;3) $ appartiene all'iperbole.
Una volta verificato questo, posso applicare la formula di sdoppiamento sostituendo $ x^2 \rightarrow xx_0 $ e $ y^2 \rightarrow yy_0 $ all'equazione canonica dell'iperbole.
$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$
$$ \frac{xx_0}{4} - \frac{yy_0}{3} = 1 $$
Le coordinate del punto di tangenza sono $ P(4;3) $ ossia $ x_0 = 4 $ e $ y_0 = 3 $
$$ \frac{x \cdot 4}{4} - \frac{y \cdot 3}{3} = 1 $$
$$ x - y = 1 $$
$$ y = x - 1 $$
Quindi, la retta tangente al punto $ P(4;3) $ è la retta $ y = x - 1 $
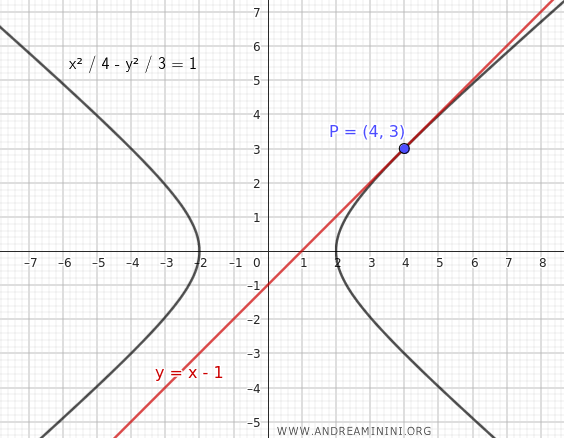
E così via.
