L'equazione dell'iperbole

Dove \(a\) è la distanza dal centro $ O $ dell'iperbole ai vertici lungo l'asse delle \(x\) mentre \(b\) è la distanza associata all'asse delle \(y\), che determina la forma dell'iperbole.

In entrambi i casi l'iperbole si presenta come una curva aperta e simmetrica rispetto all'asse x, all'asse y e all'origine, costituita da due rami simmetrici rispetto agli assi di simmetria.

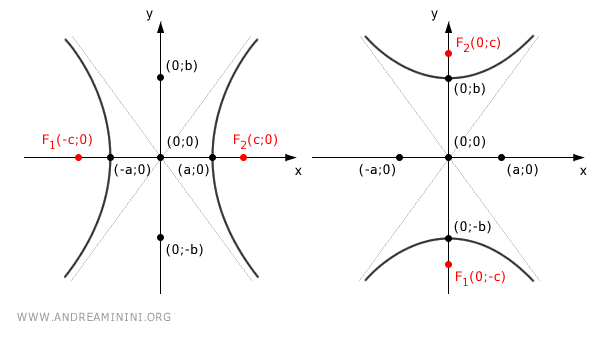
Il centro dell'iperbole \((0, 0)\) nella forma standard, è il punto di simmetria dell'iperbole dove passano due rette, dette asintoti, a cui l'iperbole si avvicina sempre di più ma che non raggiunge mai.

Le equazioni degli asintoti dell'iperbole sono:

$$ y = \pm \frac{b}{a} x $$

Gli asintoti formano un angolo con gli assi e rappresentano le direzioni verso cui i rami dell'iperbole si dirigono all'infinito.

 

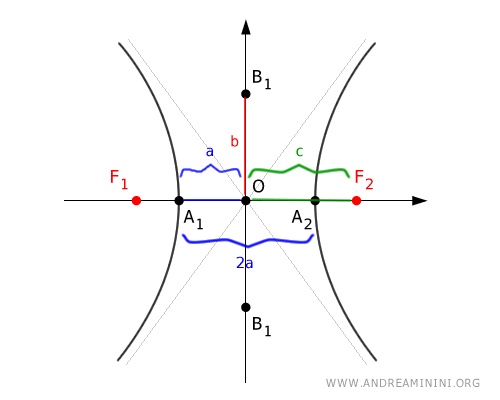
L'iperbole è formata da due rami che si estendono all'infinito, ognuno dei quali si avvicina ai suoi asintoti.

I fuochi sono due punti fissi interni all'iperbole situati lungo l'asse delle \(x\) o sull'asse delle \( y \), la cui differenza in valore assoluto delle distanze da qualsiasi punto $ P(x;y) $ dell'iperbole è costante ed è pari a $ 2a $

$$ | \overline{PF_1} - \overline{PF_2} |  = 2a $$

Nota. Se l'iperbole ha i fuochi sull'asse verticale y vale la relazione $$ | \overline{PF_1} - \overline{PF_2} |  = 2b $$

Le coordinate dei fuochi sono:

• Se i fuochi si trovano sull'asse x:  $$ F_1(-c;0) $$ $$ F_2(c;0) $$
• Se i fuochi si trovano sull'asse y: $$ F_1(0;-c) $$ $$ F_2(0;c) $$

Dove $ c $ è la distanza di un fuoco dal centro mentre $ a $ e $ b $ sono quelle dei vertici rispetto al centro e tra queste vale la relazione seguente:

$$ c = \sqrt{a^2+b^2} $$

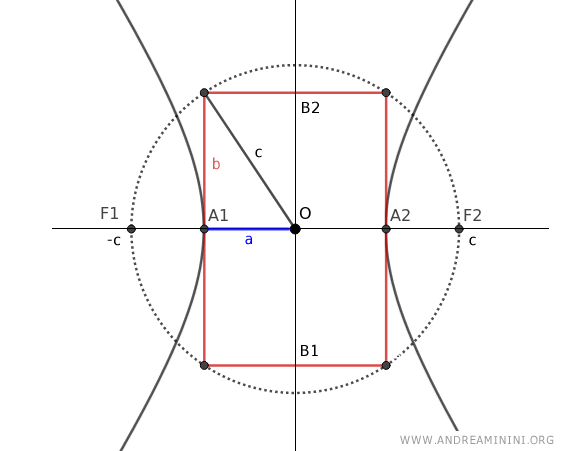
Spiegazione. Traccio una circonferenza centrata nel centro O dell'iperbole con raggio "c" e un rettangolo con lati 2a e 2b centrato sul centro dell'iperbole. Poi costruisco un triangolo rettangolo che ha il raggio "c" come ipotenusa e i lati "a" e "b" come cateti. Quindi, per il teorema di Pitagora c²=a²+b².

L'asse dove passano i fuochi è detto asse trasverso, mentre l'altro asse perpendicolare è detto asse non trasverso.

Le intersezioni dell'iperbole con l'asse trasverso sono dette vertici e sono:

• Se i fuochi si trovano sull'asse x:  $$ A_1(-a;0) $$ $$ A_2(a;0) $$
• Se i fuochi si trovano sull'asse y:  $$ B_1(0;-b) $$ $$ B_2(0;b) $$

Spiegazione. Per trovare le coordinate dei vertici in un'iperbole con l'asse trasverso x basta sostituire y=0 nell'equazione canonica dell'iperbole. $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ $$ \frac{x^2}{a^2} - \frac{0^2}{b^2} = 1 $$ $$ \frac{x^2}{a^2} = 1 $$ $$ x^2 = a^2 $$ $$ x = a $$ Analogamente per trovare le coordinate dei vertici in un'iperbole con l'asse trasverso y sostituisco x=0 nell'equazione canonica dell'iperbole. $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$ $$ \frac{0^2}{a^2} - \frac{y^2}{b^2} = -1 $$ $$ - \frac{y^2}{b^2} = -1 $$ $$ - y^2 = - b^2 $$ $$  y^2 =  b^2 $$ $$ y = b $$

I vertici che si trovano sull'asse trasverso sono detti vertici reali dell'iperbole, mentre quelli che si trovano sull'asse non trasverso sono detti vertici non reali.

L'eccentricità dell'iperbole è il rapporto tra la distanza focale $ c $ e la lunghezza dell'asse trasverso $ a $ o $ b $

• Se l'asse trasverso è l'asse x $$ e = \frac{c}{a} $$
• Se l'asse trasverso è l'asse y $$ e = \frac{c}{b} $$

Poiché in un iperbole $ c > a $ se l'asse trasverso è l'asse x e $ a > 0 $ deduco che l'eccentricità $ e = \frac{c}{a} $ è sempre maggiore di 1 $ e > 1 $

Nota. Lo stesso accade se l'asse trasverso è l'asse y, in questo caso $ c > b $  e $ b > 0 $, pertanto l'eccentricità $ e = \frac{c}{b} $ è sempre maggiore di 1 $ e > 1 $

Ogni iperbole ha due fuochi e due rette direttrici che sono simmetriche, parallele tra loro e perpendicolari rispetto all'asse trasverso.

Se l'asse trasverso, quello coni fuochi, coincide con l'asse \(x\), le rette direttrici sono date da:

$$ x = \pm \frac{a^2}{c} $$

Nel caso in cui l'asse trasverso sia l'asse \(y\), invece, le rette direttrici sono espresse nel seguente modo:

$$ y = \pm \frac{b^2}{c} $$

In generale, come accade per qualsiasi conica, dato un punto \( P(x;y) \) dell'iperbole, il rapporto tra la distanza \( \overline{PF} \) del punto dal fuoco e la distanza \( \overline{PH} \) del punto dalla retta direttrice è costante e corrisponde all'eccentricità dell'iperbole:

$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$

Ecco un esempio pratico delle rette direttrici di un'iperbole.

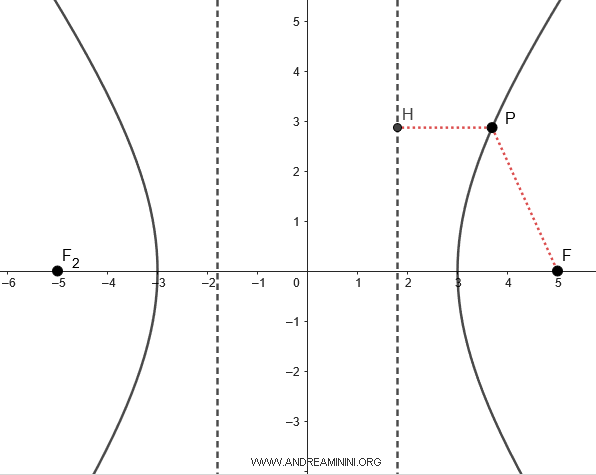
Dimostrazione. Considero un'iperbole con l'asse trasverso sull'asse x. $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ Le rette direttrici sono perpendicolari all'asse x $$ x = k $$ Per definizione, il rapporto la distanza tra un punto dell'iperbole e il fuoco e la distanza tra lo stesso punto e la retta direttrice è costante ed è uguale all'eccentricità. $$ \frac{ \overline{PF} }{ \overline{PH} } = e $$ Dove l'eccentricità è il rapporto $ e=\frac{c}{a} $ $$ \frac{ \overline{PF} }{ \overline{PH} } = \frac{c}{a} $$ Scelgo come punto $ P $ il vertice $ A(a,0) $ dell'iperbole. Quindi la distanza $ \overline{PF} = c-a $ mentre la distanza $ \overline{PH} = a-k $ $$ \frac{ c-a }{ a-k } = \frac{c}{a} $$ $$ a \cdot (c-a)= c \cdot (a-k) $$ $$ \require{cancel} \cancel{ac} -a^2 = \cancel{ac} - kc $$ $$ - a^2 \cdot (-1) = - kc \cdot (-1) $$ $$ a^2 = kc $$ $$ k = \frac{a^2}{c} $$ Poiché l'altra retta direttrice è parallela e simmetrica, le due rette direttrici si trovano sull'asse x nei punti $ (k;0) $ e $ (-k;0) $. Allo stesso modo si dimostra che se l'asse trasverso è sull'asse y, le rette direttrici sono $ y = \pm \frac{b^2}{c} $

Esempio Pratico

Immagino di avere un'iperbole con \(a = 3\) e \(b = 4\) con i fuochi sull'asse $ x $.

L'equazione dell'iperbole è

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{3^2} - \frac{y^2}{4^2} = 1 $$

$$ \frac{x^2}{9} - \frac{y^2}{16} = 1 $$

Per comprendere meglio, traccio questa iperbole su un piano cartesiano.

I vertici dell'iperbole si trovano a \((\pm 3, 0)\).

Gli asintoti sono determinati dalle equazioni 

$$ y = \pm \frac{4}{3} x $$

Tracciando queste linee e disegnando i rami dell'iperbole che si avvicinano agli asintoti, ottengo la rappresentazione grafica dell'iperbole.

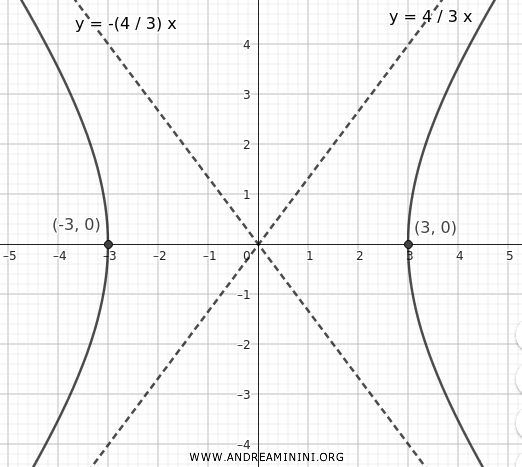
I fuochi si trovano sull'asse x quindi si trovano alle coordinate

$$ F_1(-c;0) $$

$$ F_1(c;0) $$

Dove $ c^2 = a^2+b^2 $

$$ c^2 = a^2 + b^2 $$

$$ \sqrt{c^2} = \sqrt{a^2 + b^2} $$

$$ c = \sqrt{a^2 + b^2} $$

Sapendo che $ a^2 = 9 $ e $ b^2 = 16 $

$$ c = \sqrt{9 + 16} $$

$$ c = \sqrt{25} $$

$$ c = 5 $$

Quindi, i fuochi si trovano alle coordinate:

$$ F_1(-5;0) $$

$$ F_1(5;0) $$

Ecco la rappresentazione grafica

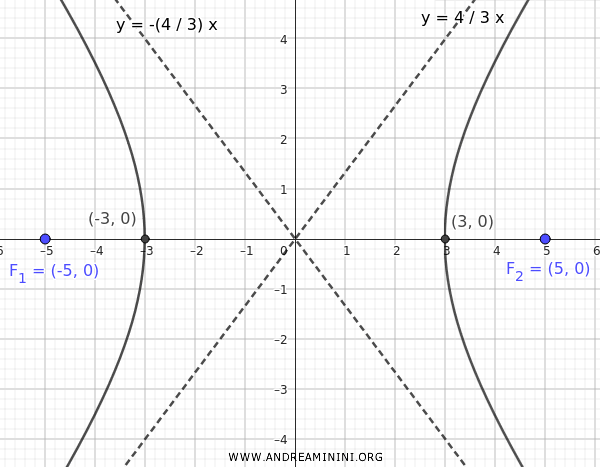
In questo caso l'asse trasverso, quello con i fuochi, coincide con l'asse x.

Quindi, le rette direttrici sono espresse in questo modo:

$$ x = \pm \frac{a^2}{c}  $$

Dove $ a=3 $ e $ c=5 $

$$ x = \pm \frac{a^2}{c} = \pm \frac{3^2}{5} = \pm \frac{9}{5} = \pm 1.8  $$

Il rapporto tra le distanze $ \overline{PF} $ e $ \overline{PH} $ è costante per qualsiasi punto $ P(x;y) $ dell'iperbole ed è uguale all'eccentricità ( e ).

$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$

Ad esempio, nel caso del punto $ P $ la distanza tra il punto e il fuoco è $ \overline{PF} = 4.09  $ mentre quella dallo stesso punto e la retta direttrice è $ \overline{PH} = 2.46  $

$$ e = \frac{ \overline{PF} }{ \overline{PH} } = \frac{4.09}{2.46} \approx 1.67 $$

Pertanto, l'eccentricità dell'iperbole è $ e \approx 1.67 $

Il rapporto $ e = \frac{ \overline{PF} }{ \overline{PH} } $ è uguale in qualsiasi altro punto dell'iperbole.

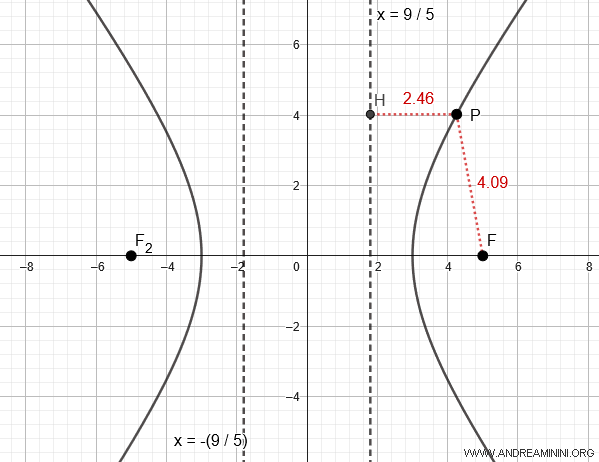
Nota. Un altro modo per calcolare l'eccentricità dell'iperbole è la formula $$ e = \frac{c}{a} = \frac{5}{3} \approx 1.67 $$ Il risultato finale è lo stesso.

La dimostrazione

Considero il caso in cui i fuochi F1(-c;0) e F2(c;0) siano allineati sull'asse x delle ascisse e il centro dell'iperbole sia l'origine degli assi cartesiani.

Per trovare l'equazione canonica dell'iperbole, scelgo un qualsiasi punto P(x;y) dell'iperbole

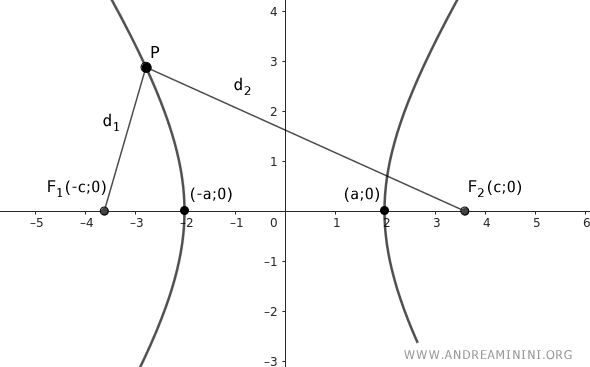
In una iperbole la differenza delle distanze del punto tra i due fuochi è uguale a 2a.

$$ \overline{PF_1} - \overline{PF_2} = 2a $$

Perché la differenza delle distanze è uguale a 2a? Per definizione in qualsiasi punto di un'iperbole la differenza delle distanze è costante in valore assoluto e i fuochi si trovano alla distanza "c" dal centro.

Se considero il punto A₂, la distanza del punto dal fuoco F₂ è c-a e dal fuoco F₁ è a+c $$ \overline{A_2F_2} = c-a $$ $$ \overline{A_2F_1} = a+c $$ Ora calcolo la differenza tra le distanze $$ \overline{A_2F_1} - \overline{A_2F_2} = k $$ $$ (a+c) - (c-a) = k $$ $$ a+c-c+a = k $$ $$ 2a = k $$

Tornando al punto P

Utilizzo il teorema di Pitagora per calcolare le distanze del punto P dai fuochi.

$$ d_1 = \overline{PF_1} = \sqrt{(x-(-c))^2+(y-0)^2} = \sqrt{(x+c)^2+y^2}  $$

$$ d_2 = \overline{PF_2} = \sqrt{(x-c)^2+(y-0)^2} = \sqrt{(x-c)^2+y^2} $$

Quindi, posso scrivere la differenza delle distanze anche in questo modo equivalente.

$$ \overline{PF_1} - \overline{PF_2} = 2a $$

$$ \sqrt{(x+c)^2+y^2} - \sqrt{(x-c)^2+y^2} = 2a $$

Sposto una delle due radici nel membro a destra.

$$ \sqrt{(x+c)^2+y^2} = 2a + \sqrt{(x-c)^2+y^2} $$

Poi elevo entrambi i membri dell'equazione alla seconda.

$$ ( \sqrt{(x+c)^2+y^2} ) = ( 2a + \sqrt{(x-c)^2+y^2} )^2 $$

$$ (x+c)^2+y^2 = (2a)^2 + 2 \cdot ( 2a \sqrt{(x-c)^2+y^2} ) + (\sqrt{(x-c)^2+y^2} )^2 $$

$$ (x+c)^2+y^2 = (2a)^2 + 2 \cdot ( 2a \sqrt{(x-c)^2+y^2} ) + (\sqrt{(x-c)^2+y^2} )^2 $$

$$ (x+c)^2+y^2 = 4a^2 + 4a \sqrt{(x-c)^2+y^2} + (x-c)^2+y^2 $$

$$ (x+c)^2 = 4a^2 + 4a \sqrt{(x-c)^2+y^2} + (x-c)^2 $$

Ora sviluppo il quadrato dei binomi (x+c)² e (x-c)² fuori dalla radice e semplifico

$$ x^2+2xc+c^2 = 4a^2 + 4a \sqrt{(x-c)^2+y^2} + x^2-2xc+c^2 $$

$$ 2xc = 4a^2 + 4a \sqrt{(x-c)^2+y^2} -2xc $$

$$ 2xc - 4a^2 +2xc = 4a \sqrt{(x-c)^2+y^2} $$

$$ 4xc - 4a^2 = 4a \sqrt{(x-c)^2+y^2} $$

Divido entrambi i membri dell'equazione per 4

$$ \frac{ 4xc - 4a^2}{4} = \frac{ 4a \sqrt{(x-c)^2+y^2} }{4} $$

$$ xc - a^2 = a \sqrt{(x-c)^2+y^2} $$

Elevo al quadrato entrambi i membri dell'equazione per togliere la radice.

$$ ( xc - a^2 )^2 = ( a \sqrt{(x-c)^2+y^2} )^2 $$

$$ x^2c^2-2xca^2+a^4 = a^2 \cdot [(x-c)^2+y^2 ] $$

$$ x^2c^2-2xca^2+a^4 = a^2 \cdot ( x^2-2xc+c^2+y^2 ) $$

$$ x^2c^2-2xca^2+a^4 = x^2a^2-2xca^2+a^2c^2+a^2y^2 $$

Poi semplifico

$$ x^2c^2+a^4 = x^2a^2+a^2c^2+a^2y^2 $$

Divido entrambi i membri dell'equazione per a²

$$ \frac{ x^2c^2+a^4}{a^2} = \frac{ x^2a^2+a^2c^2+a^2y^2 }{a^2} $$

$$ \frac{x^2c^2}{a^2}+a^2 = x^2+c^2+y^2 $$

Sposto i termini noti del membro di destra dell'equazione e le incognite a sinistra.

$$ \frac{x^2c^2}{a^2} -x^2 -y^2= c^2-a^2 $$

Metto in evidenza x²

$$ x^2 \cdot ( \frac{c^2}{a^2} - 1) -y^2 = c^2-a^2 $$

$$ x^2 \cdot ( \frac{c^2-a^2}{a^2}) -y^2 = c^2-a^2 $$

A questo punto, sapendo che c>a pongo c²-a²=b²

$$ x^2 \cdot ( \frac{b^2}{a^2}) -y^2 = b^2 $$

$$ \frac{x^2b^2}{a^2} -y^2 = b^2 $$

Spiegazione. Costruisco un rettangolo con lati 2a e 2b centrato sul centro dell'iperbole, poi traccio una diagonale e ottengo un triangolo rettangolo che ha "c" per ipotenusa mentre "a" e "b" sono i cateti. Per il teorema di Pitagora c²=a²+b². Quindi, c²-a²=b².

Poi divido entrambi i membri dell'equazione per b²

$$ \frac{1}{b^2} \cdot [ \frac{x^2b^2}{a^2} -y^2 ] = \frac{1}{b^2} \cdot b^2 $$

$$ \frac{ x^2b^2 }{a^2b^2} - \frac{ y^2 }{b^2} = 1 $$

$$ \frac{ x^2 }{a^2} - \frac{ y^2 }{b^2} = 1 $$

Il risultato finale è l'equazione canonica dell'iperbole quando i fuochi si trovano sull'asse x e il centro dell'ellisse coincide con l'origine O(0;0) degli assi cartesiani.

E così via.