Equazione dell'iperbole data l'eccentricità e un vertice
Per scrivere l'equazione di una iperbole centrata nell'origine degli assi cartesiani conoscendo l'eccentricità e un vertice $ A(a;0) $ oppure $ B(0;b) $, seguo questi passaggi:
- Se i fuochi si trovano sull'asse x, l'equazione dell'iperbole è $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ mentre l'eccentricità è $$ e= \frac{c}{a} $$
- Se i fuochi si trovano sull'asse y, l'equazione dell'iperbole è $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$ mentre l'eccentricità è $$ e= \frac{c}{b} $$
In entrambi i casi la relazione tra i semiassi $ a $, $ b $ e la distanza del fuoco dal centro dell'iperbole $ c $ è la seguente:
$$ c^2 = a^2 + b^2 $$
Nota. Se il problema non consente di capire qual è l'asse trasverso, quello in cui si trovano i fuochi, vanno considerate entrambe le ipotesi: asse trasverso sull'asse x e asse trasverso sull'asse y.
Un esempio pratico
Considero un'iperbole centrata nell'origine con un vertice non reale nel punto $ A(-2;0) $ e l'eccentricità $ e = \frac{3 \sqrt{5}}{5} $
Il vertice $ A(-2;0) $ si trova sull'asse x e il problema cita espressamente che non è "reale", quiindi l'asse reale dove ci sono anche i fuochi e l'asse y.
Quando l'asse reale (trasverso) è l'asse y, l'equazione dell'iperbole è la seguente:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
L'eccentricità dell'iperbole è invece la seguente:
$$ e = \frac{c}{b} $$
Metto le due equazioni in un sistema
$$ \begin{cases} e = \frac{c}{b} \\ \\ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 \end{cases} $$
Conosco l'eccentricità $ e = \frac{3 \sqrt{5}}{5} $ e le coordinate di un vertice $ A(a;0)=(2;0) $ quindi $ a=2 $
$$ \begin{cases} \frac{3 \sqrt{5}}{5} = \frac{c}{b} \\ \\ \frac{x^2}{2^2} - \frac{y^2}{b^2} = 1 \end{cases} $$
$$ \begin{cases} \frac{3 \sqrt{5}}{5} = \frac{c}{b} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
Sapendo che $ c^2 = a^2+b^2 $ allora $ c = \sqrt{a^2+b^2} $ con $ a=2 $
$$ \begin{cases} \frac{3 \sqrt{5}}{5} = \frac{\sqrt{a^2+b^2}}{b} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{3 \sqrt{5}}{5} = \frac{\sqrt{2^2+b^2}}{b} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{3 \sqrt{5}}{5} = \frac{\sqrt{4+b^2}}{b} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
Elevo al quadrato entrambi i lati della prima equazione
$$ \begin{cases} ( \frac{3 \sqrt{5}}{5} )^2 = ( \frac{\sqrt{4+b^2}}{b} )^2 \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{9 \cdot 5}{25} = \frac{4+b^2}{b^2} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{9}{5} = \frac{4}{b^2} + \frac{b^2}{b^2} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{9}{5} = \frac{4}{b^2} + 1 \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{9}{5} - 1 = \frac{4}{b^2} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{9-5}{5} = \frac{4}{b^2} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{4}{5} = \frac{4}{b^2} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} b^2 = \frac{5}{4} \cdot 4 \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} b^2 = 5 \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \sqrt{b^2} = \sqrt{5} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} b = \sqrt{5} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
Una volta noto $ b = \sqrt{5} $ posso sostituirlo nella seconda equazione
$$ \begin{cases} b = \sqrt{5} \\ \\ \frac{x^2}{4} - \frac{y^2}{(\sqrt{5})^2} = -1 \end{cases} $$
$$ \begin{cases} b = \sqrt{5} \\ \\ \frac{x^2}{4} - \frac{y^2}{5} = -1 \end{cases} $$
Quindi, l'equazione dell'iperbole centrata nell'origine con un vertice non reale nel punto $ A(-2;0) $ e l'eccentricità $ e = \frac{3 \sqrt{5}}{5} $ è la seguente:
$$ \frac{x^2}{4} - \frac{y^2}{5} = -1 $$
Ecco la rappresentazione grafica:
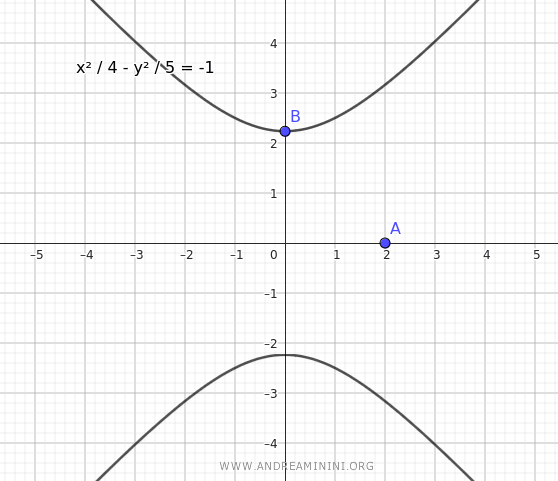
E così via.
