Iperbole centrata in un punto diverso dall'origine
L'equazione di un'iperbole traslata con centro nel punto \((p, q)\) si ottiene semplicemente traslando l'iperbole canonica centrata nell'origine \((0, 0)\).
- Iperbole con asse reale sull'asse \(x\):
L'equazione canonica di un'iperbole centrata nell'origine con l'asse reale sull'asse \(x\) è: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ Se si trasla il centro dell'iperbole da \((0, 0)\) a \((p, q)\), l'equazione diventa: $$
\frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} = 1 $$ - Iperbole con asse reale sull'asse \(y\):
L'equazione canonica di un'iperbole centrata nell'origine con l'asse reale sull'asse \(y\) è: $$
\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1 $$ Traslando il centro dell'iperbole a \((p, q)\), l'equazione diventa: $$
\frac{(y-q)^2}{a^2} - \frac{(x-p)^2}{b^2} = 1 $$
In entrambi i casi, \(a\) rappresenta la distanza dal centro ai vertici lungo l'asse reale, mentre \(b\) è la distanza dal centro agli estremi dell'asse trasverso (asse immaginario).
L'equazione generale di un'iperbole traslata
L'equazione generale di una conica è data dalla forma:
$$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$
In questa forma, \(Ax^2\) e \(Cy^2\) rappresentano i termini quadratici, \(Bxy\) è il termine misto, e \(Dx\) e \(Ey\) sono i termini lineari. \(F\) è un termine costante.
Per ottenere questa forma da un'equazione di un'iperbole centrata nel punto \((p, q)\) come:
$$ \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} = 1 $$
Espando l'equazione canonica dell'iperbole, sviluppando i quadrati:
$$ \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} = 1 $$
$$ \frac{(x^2 - 2px + p^2)}{a^2} - \frac{(y^2 - 2qy + q^2)}{b^2} = 1 $$
Moltiplico entrambi i membri per \(a^2b^2\) per eliminare i denominatori:
$$ b^2(x^2 - 2px + p^2) - a^2(y^2 - 2qy + q^2) = a^2b^2 $$
$$ b^2x^2 - 2b^2px + b^2p^2 - a^2y^2 + 2a^2qy - a^2q^2 = a^2b^2 $$
Porto tutti i termini al primo membro:
$$ b^2x^2 - a^2y^2 - 2b^2px + 2a^2qy + (b^2p^2 - a^2q^2 - a^2b^2) = 0 $$
Confrontando con la forma generale \(Ax^2 + By^2 + Cx + Dy + E = 0\), i coefficienti sono:
- \(A = b^2\)
- \(B' = -a^2\)
- \(C = -2b^2p\)
- \(D = 2a^2q\)
- \(E = b^2p^2 - a^2q^2 - a^2b^2\)
Questa è la forma espansa dell'equazione di un'iperbole traslata. Ogni termine rappresenta un componente dell'equazione generale di una conica centrata non sull'origine.
Un esempio pratico
Faccio un esempio pratico di un'iperbole traslata.
Supponiamo di partire dall'equazione canonica di un'iperbole con asse reale sull'asse \(x\) (quindi orizzontale) e centro nell'origine \((0, 0)\):
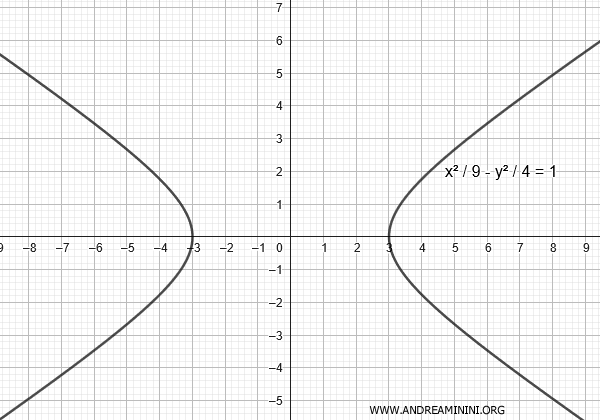
$$ \frac{x^2}{9} - \frac{y^2}{4} = 1 $$
Questa è un'iperbole orizzontale con \(a^2 = 9\) (quindi \(a = 3\)) e \(b^2 = 4\) (quindi \(b = 2\)).
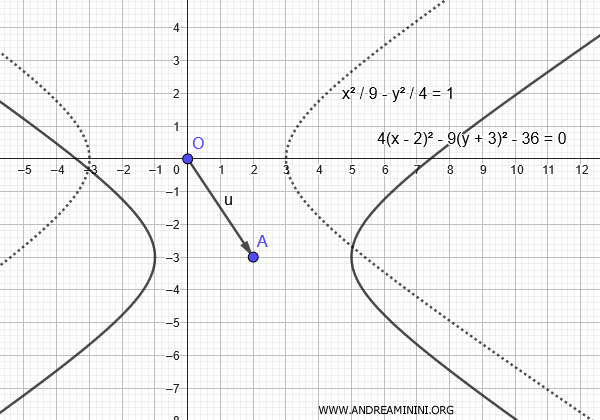
Voglio traslare il centro dell'iperbole dal punto \((0, 0)\) al punto \((p, q) = (2, -3)\).
L'equazione dell'iperbole traslata diventa:
$$ \frac{(x - 2)^2}{9} - \frac{(y + 3)^2}{4} = 1 $$
Ora espando questa equazione per ottenere la forma generale:
$$ \frac{(x^2 - 4x + 4)}{9} - \frac{(y^2 + 6y + 9)}{4} = 1 $$
Moltiplico entrambi i membri per 36 (che è il minimo comune multiplo di 9 e 4) per eliminare i denominatori:
$$ 4(x^2 - 4x + 4) - 9(y^2 + 6y + 9) = 36 $$
Espando e semplifico:
$$ 4x^2 - 16x + 16 - 9y^2 - 54y - 81 = 36 $$
Porto tutti i termini al primo membro:
$$ 4x^2 - 9y^2 - 16x - 54y + 16 - 81 - 36 = 0 $$
Semplifico i termini costanti:
$$ 4x^2 - 9y^2 - 16x - 54y - 101 = 0 $$
Questa è l'equazione dell'iperbole traslata con centro nel punto \((2, -3)\) e gli stessi valori di \(a^2\) e \(b^2\) dell'iperbole originaria.
Le coordinate del centro dell'iperbole
Le coordinate del centro di un'iperbole non centrata nell'origine $$ Ax^2 + By^2 + Cx + Dy + E = 0 $$ si ottengono usando questa formula $$ \left(p, q\right) = \left(-\frac{C}{2A}, - \frac{D}{2B}\right) $$
Esempio
L'equazione generale di un'iperbole non centrata nell'origine è:
$$ 4x^2 - 9y^2 - 16x - 54y - 101 = 0 $$
In questo caso $ A=4 $ , $ B=-9 $, $C=-16 $, $D =-54 $, $ E=-101 $
Quindi le coordinate del centro sono le seguenti:
$$ \left(p, q\right) = \left(-\frac{C}{2A}, - \frac{D}{2B}\right) $$
$$ \left(p, q\right) = \left(-\frac{-16}{2 \cdot 4}, - \frac{-54}{2 \cdot (-9)}\right) $$
$$ \left(p, q\right) = \left(\frac{16}{8}, - \frac{54}{18}\right) $$
$$ \left(p, q\right) = \left( 2, -3\right) $$
Dimostrazione
Considero l'equazione di un'iperbole non centrata nell'origine nella forma generale:
$$ Ax^2 + By^2 + Cx + Dy + E = 0 $$
Raggruppo i termini quadratici e lineari:
$$ (Ax^2 + Cx)+ (By^2 + Dy) = -E $$
Completo il quadrato per i termini in \(x\) e in \(y\):
- Per il termine in \(x\)
Considero i termini con la \( x \) ossia \(Ax^2 + Cx\) e fattorizzo per \(A\): $$
A\left(x^2 + \frac{C}{A}x\right) $$ Completo il quadrato aggiungendo e sottraendo \(\left(\frac{C}{2A}\right)^2\): $$
A\left(x^2 + \frac{C}{A}x + \left(\frac{C}{2A}\right)^2 - \left(\frac{C}{2A}\right)^2\right) = A\left(\left(x + \frac{C}{2A}\right)^2 - \left(\frac{C}{2A}\right)^2\right) $$ Questo diventa: $$ A\left(x + \frac{C}{2A}\right)^2 - A\left(\frac{C}{2A}\right)^2 $$ - Per il termine in \(y\)
Considero i termini con la \( y \) ossia \(By^2 + Dy\) e fattorizzo per \(B\): $$ B\left(y^2 + \frac{D}{B}y\right) $$ Completo il quadrato aggiungendo e sottraendo \(\left(\frac{D}{2B}\right)^2\): $$ B\left(y^2 + \frac{D}{B}y + \left(\frac{D}{2B}\right)^2 - \left(\frac{D}{2B}\right)^2\right) = B\left(\left(y + \frac{D}{2B}\right)^2 - \left(\frac{D}{2B}\right)^2\right) $$ Questo diventa: $$ B\left(y +\frac{D}{2B}\right)^2 + B\left(\frac{D}{2B}\right)^2$$
Sostituisco i quadrati completati:
$$ Ax^2 + Cx + By^2 + Dy = -E $$
$$ (Ax^2 + Cx) + ( By^2 + Dy) = -E $$
$$ A\left(x^2 + \frac{C}{A}x\right) + B\left(y^2 + \frac{D}{B}y\right) = -E $$
$$ A\left(x + \frac{C}{2A}\right)^2 - A\left(\frac{C}{2A}\right)^2 + B\left(y + \frac{D}{2B}\right)^2 - B\left(\frac{D}{2B}\right)^2 = E $$
$$ A\left(x + \frac{C}{2A}\right)^2 + B\left(y + \frac{D}{2B}\right)^2 = E + A\left(\frac{C}{2A}\right)^2 + B\left(\frac{D}{2B}\right)^2 $$
L'equazione ora è in una forma che mostra chiaramente la traslazione, quindi il centro dell'iperbole è dato da:
$$ \left(-\frac{C}{2A},- \frac{D}{2B}\right) $$
Questo dimostra che le coordinate del centro sono:
$$ \left(p, q\right) = \left(-\frac{C}{2A}, - \frac{D}{2B}\right) $$
Gli assi di simmetria
Gli assi di simmetria di un'iperbole non centrata nell'origine $$ Ax^2 + By^2 + Cx + Dy + E = 0 $$ sono le componenti del centro $ (p,q) $ ossia $$ x = p = -\frac{C}{2A} $$ $$ y = q = - \frac{D}{2B} $$
Esempio
L'equazione generale di un'iperbole non centrata nell'origine è:
$$ 4x^2 - 9y^2 - 16x - 54y - 101 = 0 $$
In questo caso $ A=4 $ , $ B=-9 $, $C=-16 $, $D =-54 $, $ E=-101 $
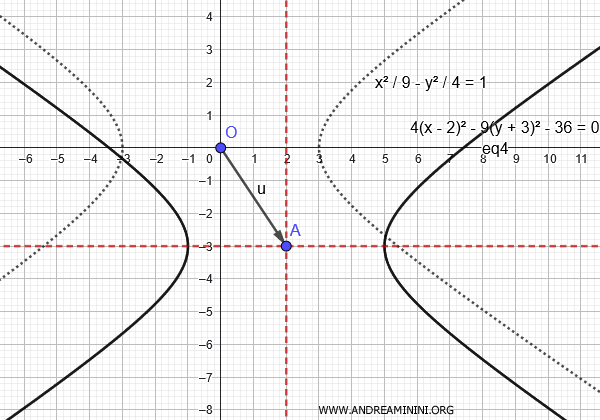
Gli assi di simmetria dell'iperbole sono
$$ x = p = -\frac{C}{2A} = -\frac{-16}{2 \cdot 4} = 2 $$
$$ y = q = - \frac{D}{2B} =- \frac{-54}{2 \cdot (-9)} = -3 $$
Dimostrazione
Gli assi di simmetria dell'iperbole corrispondono alle rette passanti per il centro e parallele agli assi coordinati o inclinate rispetto a questi nel caso in cui l'iperbole sia ruotata.
Quindi, se l'iperbole non èn ruotata, cioè gli assi sono paralleli agli assi cartesiani, le equazioni degli assi di simmetria sono:
$$ x = p $$
$$ y = q $$
Dove \((p, q)\) è il centro dell'iperbole.
Nota. Se l'iperbole è ruotata, le equazioni degli assi di simmetria possono essere ottenute dalla trasformazione che coinvolge l'angolo di rotazione \(\theta\) derivato dai coefficienti \(A\), \(B\), e dai termini di misto (se presenti) nell'equazione generale. In generale, si tratta di risolvere l'equazione per trovare la direzione degli assi di simmetria.
E così via.
