Le rette tangenti all'iperbole

Per trovare le rette tangenti a un'iperbole che passano per un punto P(x0;y0), costruisco un sistema con l'equazione dell'iperbole e l'equazione del fascio di rette che passano per il punto P.

$$ \begin{cases} \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 \\ \\ y-y_0 = m (x-x_0) \end{cases} $$

Il sistema mi permette di trovare un'equazione risolvente di secondo grado nella variabile y.

Per trovare le rette tangenti, impongo la condizione di tangente $ \Delta = 0 $ all'equazione risolvente e la risolvo rispetto al coefficiente angolare m.

• Se l'equazione ha due soluzioni reali m₁≠m₂, allora esistono due rette tangenti all'iperbole che passano il punto P(x₀;y₀) e quest'ultimo è un punto esterno all'iperbole.
  
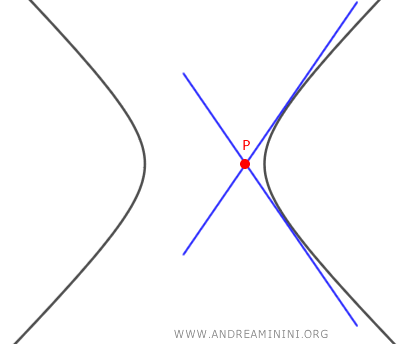
• Se l'equazione ha una sola soluzione reale m₁=m₂, allora esiste una retta tangente all'iperbole che passa il punto P(x₀;y₀) e quest'ultimo è un punto dell'iperbole.
  
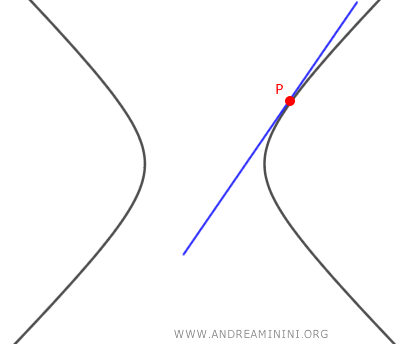
• Se l'equazione non ha soluzioni reali, allora non esistono rette tangenti all'iperbole passanti per il punto P(x₀;y₀).
  

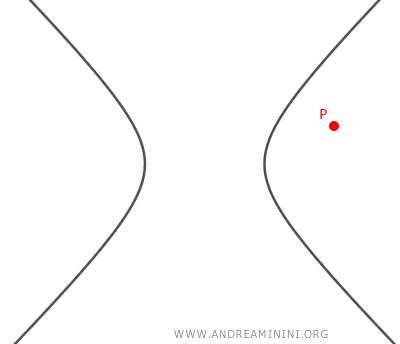
Esempio pratico

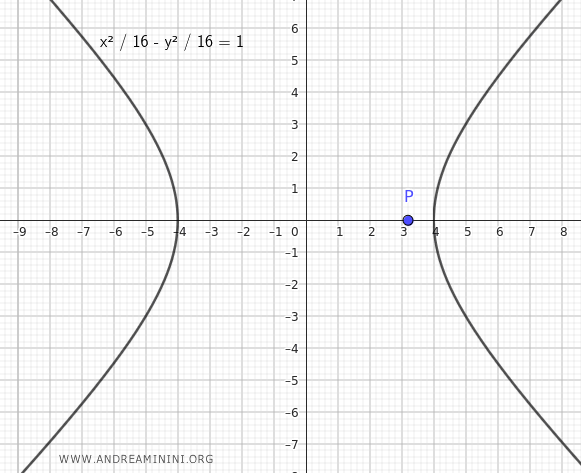
Considero un'equazione

$$ \frac{x^2}{16} - \frac{y^2}{16} = 1 $$

Devo trovare la tetta o le rette tangenti che passano per il punto $ P( \frac{16}{5};0) $

Per prima cosa scrivo un sistema con l'equazione dell'iperbole e l'equazione del fascio di rette che passa per $ P( \frac{16}{5};0) $

$$ \begin{cases} \frac{x^2}{16} - \frac{y^2}{16} = 1 \\ \\ (y-y_0)=m(x-x_0) \end{cases} $$

In questo caso le coordinate del punto sono $ x_0 = \frac{16}{5} $ e $ y_0 = 0 $

$$ \begin{cases} \frac{x^2}{16} - \frac{y^2}{16} = 1 \\ \\ (y-0)=m(x-\frac{16}{5}) \end{cases} $$

$$ \begin{cases} \frac{x^2}{16} - \frac{y^2}{16} = 1 \\ \\ y=mx-\frac{16m}{5} \end{cases} $$

Ricavo la variabile y in entrambe le equazioni

$$ \begin{cases} y^2 = 16 \cdot ( \frac{x^2}{16} -1 ) \\ \\ y=mx-\frac{16m}{5} \end{cases} $$

$$ \begin{cases} y^2 = x^2 - 16 \\ \\ y=mx-\frac{16m}{5} \end{cases} $$

$$ \begin{cases} y = \sqrt{ x^2 - 16 } \\ \\ y=mx-\frac{16m}{5} \end{cases} $$

L'equazione risolvente del sistema è la seguente:

$$ \sqrt{ x^2 - 16 } = mx-\frac{16m}{5} $$

$$ (\sqrt{ x^2 - 16 })^2 = ( mx-\frac{16m}{5})^2 $$

$$ x^2 - 16  = (mx)^2 - 2 \cdot mx \cdot \frac{16m}{5} +(\frac{16m}{5})^2 $$

$$ x^2 - 16  = m^2x^2 - \frac{32m^2x}{5} + \frac{256m^2}{25} $$

$$ x^2 - 16  - m^2x^2 + \frac{32m^2x}{5} - \frac{256m^2}{25} = 0 $$

$$ x^2 (1- m^2  ) + x (\frac{32m^2}{5} )   - 16   - \frac{256m^2}{25} = 0 $$

Si tratta di un'equazione di 2° grado in x.

Impongo la condizione di tangenza $ \Delta = 0 $.

$$ \Delta = b^2 - 4ac = 0 $$

In questo caso $ a =1- m^2  $, $ b = \frac{32m^2}{5} $, $ c = - 16  - \frac{256m^2}{25} $

$$  ( \frac{32m^2}{5} ) ^2 - 4 \cdot (1-m^2) \cdot ( - 16  - \frac{256m^2}{25} ) = 0 $$

$$  \frac{1024m^4}{25}  -  (4-4m^2) \cdot ( - 16   - \frac{256m^2}{25} ) = 0 $$

$$  \frac{1024m^4}{25}  -  4 \cdot ( - 16   - \frac{256m^2}{25} ) +4m^2 \cdot ( - 16   - \frac{256m^2}{25} ) = 0 $$

$$ \require{cancel} \cancel{  \frac{1024m^4}{25} }  + 64 + \frac{1024m^2}{25}   - 64m^2   - \cancel{ \frac{1024m^4}{25} }  = 0 $$

$$  \frac{1024m^2-1600m^2}{25}  + 64 = 0 $$

$$  - \frac{576m^2}{25}  = -64 $$

$$  m^2  = \frac{- 64 \cdot 25}{-576} $$

$$  m^2  = \frac{800}{288} $$

$$  m^2  = \frac{400}{144} $$

$$  m^2  = \frac{200}{72} $$

$$  m^2  = \frac{100}{36} $$

$$  m^2  = \frac{50}{18} $$

$$  m^2  = \frac{25}{9} $$

$$ \sqrt{  m^2 }  = \sqrt{  \frac{25}{9} } $$

$$ m  = \pm  \frac{5}{3}  $$

Una volta trovato il coefficiente angolare, lo sostituisco nell'equazione del fascio di rette.

$$ y=mx-\frac{16m}{5} $$

Devo considerare entrambi i valori del coefficiente angolare

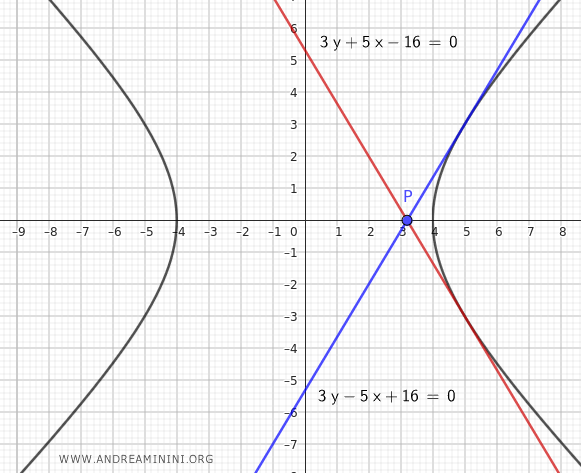
• Per $ m =\frac{5}{3} $ $$ y=\frac{5}{3}  x-\frac{16 \cdot \frac{5}{3} }{5} $$ $$ y=\frac{5}{3}  x-\frac{16 \cdot \frac{5}{3} }{5} $$ $$ y=\frac{5}{3}  x-\frac{\frac{80}{3} }{5} $$ $$ y =\frac{5}{3}  x- \frac{80}{3}  \cdot \frac{1}{5} $$ $$ y=\frac{5}{3}  x- \frac{16}{3} $$ $$ y - \frac{5}{3}  x + \frac{16}{3} = 0 $$ $$ 3 \cdot ( y - \frac{5}{3}  x + \frac{16}{3}) =  3 \cdot 0 $$ $$ 3y - 5x + 16 =  0 $$
• Per $ m = - \frac{5}{3} $ $$ y= - \frac{5}{3}  x-\frac{16 \cdot ( - \frac{5}{3} ) }{5} $$ $$ y= - \frac{5}{3}  x-\frac{ ( - \frac{80}{3} ) }{5} $$ $$ y= - \frac{5}{3}  x + \frac{80}{3} \cdot \frac{1}{5}  $$ $$ y= - \frac{5}{3}  x + \frac{16}{3} $$ $$ y + \frac{5}{3}  x - \frac{16}{3} = 0 $$ $$ 3 \cdot ( y + \frac{5}{3}  x - \frac{16}{3} )  = 3 \cdot 0 $$ $$ 3y + 5x - 16  = 0 $$

Ecco il grafico delle rette tangenti all'iperbole che passano per il punto $ P( \frac{16}{5};0) $

E così via.