Somma di sottospazi vettoriali

Dato uno spazio vettoriale V sul campo K e due sottospazi A e B di V, la somma A+B dei sottospazi è un sottospazio vettoriale composto dalla somma dei vettori di A e di B. $$A+B := \{ \vec{a}+\vec{b}, \vec{a} \in A, \vec{b} \in B \}$$ Pertanto la somma dei sottospazi contiene l'unione dei due sottospazi $$A∪B \subset A+B$$ Inoltre, A+B è il più piccolo sottospazio vettoriale che contiene l'unione dei sottospazi A∪B.

La somma di due sottospazi A+B è un sottospazio dello spazio vettoriale V.

E' detto sottoinsieme somma di V.

$$A+B \in V$$

Essendo V uno spazio vettoriale beneficia delle proprietà somma degli spazi vettoriali.

A sua volta, la somma dei sottospazi A+B contiene i due sottospazi A e B

$$A \in A+B$$

$$B \in A+B$$

Inoltre, lo spazio A+B è il più piccolo sottospazio vettoriale di V che contiene sia A che B come sottospazi.

Nota. Non lo è l'unione A∪B perché l'unione di sottospazi non è a sua volta un sottospazio vettoriale.

Dimostrazione

La somma dei sottospazi A+B è un sottospazio vettoriale

Per prima cosa devo dimostrare che la somma dei sottospazi vettoriali è un sottospazio vettoriale.

Osservo preliminarmente che i sottospazi A e B contengono il vettore nullo 0.

Quindi, anche l'insieme A+B contiene il vettore nullo.

$$\vec{a} + \vec{b} = \vec{0} + \vec{0} = \vec{0} \in A+B$$

Posso quindi procedere a verificare se rispetta le le due proprietà dei sottospazi vettoriali.

1) Proprietà della somma

Prendo due vettori generici u e w di A+B.

$$\vec{u},\vec{w} \in A+B$$

Dove u e w sono vettori ottenuti sommando un vettore di A con un vettore di B

$$\vec{u} = \vec{a_1} + \vec{b_1}$$

$$\vec{w} = \vec{a_2} + \vec{b_2}$$

con

$$\vec{a_1} \ , \ \vec{a_2} \in A$$

$$\vec{b_1} \ , \ \vec{b_2} \in B$$

La somma dei vettori

$$\vec{u} + \vec{w} = (\vec{a_1} + \vec{b_1} ) + (\vec{a_2} +\vec{b_2} )$$

Per la proprietà associativa posso riscriverla in questa forma equivalente

$$\vec{u} + \vec{w} = (\vec{a_1} + \vec{a_2} ) + ( \vec{b_1} + \vec{b_2} )$$

La somma dei vettori a₁+a₂ è un vettore somma che appartiene al sottospazio vettoriale A.

Allo stesso modo la somma dei vettori b₁+b₂ è un vettore somma del sottospazio B.

$$\vec{a_1} + \vec{a_2} \in A$$

$$\vec{b_1}+\vec{b_2} \in B$$

La somma di un vettore di A con un vettore di B appartiene all'insieme A+B

$$\vec{u} + \vec{w} = ( \vec{a_1} + \vec{a_2} ) + ( \vec{b_1} + \vec{b_2}) \in A+B$$

Pertanto, l'insieme A+B è chiuso rispetto alla somma.

E' la prima proprietà dei sottospazi vettoriali.

2) Proprietà del prodotto

Dato uno scalare k di K e la somma u+w di due elementi generici di A+B.

$$k \in K$$

$$\vec{u}+\vec{w} \in A+B$$

dove u e w sono vettori ottenuti sommando un vettore di A con un vettore di B

$$\vec{u} = \vec{a_1} +\vec{b_1}$$

$$\vec{w} = \vec{a_2} + \vec{b_2}$$

con

$$\vec{a_1}, \vec{a_2} \in A$$

$$\vec{b_1}, \vec{b_2} \in B$$

Il prodotto tra k e la somma degli elementi

$$k ( \vec{u} + \vec{w} ) = k ( \vec{a_1} + \vec{b_2} ) + k ( \vec{a_2} + \vec{b_2} )$$

può essere riscritto

$$k ( \vec{u} + \vec{w} ) = k \vec{a_1} + k \vec{b_1} + k \vec{a_2} + k \vec{b_2}$$

ossia

$$k ( \vec{u} + \vec{w} ) = k ( \vec{a_1} + \vec{a_2} ) + k ( \vec{b_1} + \vec{b_2} )$$

dove

$$k (\vec{a_1}+\vec{a_2}) \in A$$

$$k (\vec{b_1}+\vec{b_2}) \in B$$

Quindi

$$k ( \vec{u} + \vec{w} ) \in A+B$$

Il prodotto scalare ka appartiene all'insieme A+B.

Quindi, l'insieme A+B è chiuso rispetto al prodotto.

Anche la seconda proprietà dei sottospazi è soddisfatta.

Poiché sono soddisfatte entrambe le proprietà dei sottospazi vettoriali, ne consegue che la somma di due sottospazi vettoriali è un sottospazio vettoriale.

La somma dei sottospazi A+B contiene l'unione A∪B

A questo punto devo dimostrare che la somma dei sottospazi A+B contiene l'unione dei sottospazi A∪B

Ogni vettore del sottospazio A posso scriverlo come somma del vettore con il vettore nullo

$$\forall \vec{a} \in A \ \Rightarrow \vec{a} = \vec{a} + \vec{0}$$

Poiché la somma A+B è un sottospazio vettoriale, allora contiene il vettore nullo.

Quindi, il sottospazio A è contenuto nella somma A+B dei sottospazi

$$A \subset A+B$$

Posso fare la stessa considerazione anche per ogni vettore del sottospazio B

$$\forall \vec{b} \in B \ \Rightarrow \vec{a} = \vec{a} + \vec{0}$$

Quindi, anche il sottospazio B è contenuto nella somma A+B dei sottospazi

$$B \subset A+B$$

In conclusione, la somma dei sottospazi A+B contiene tutti i vettori di A e di B, ossia contiene l'unione dei sottospazi A∪B.

$$A \cup B \subset A+B$$

Un esempio pratico

Considero lo spazio vettoriale V=R³

$$V = R^3$$

e due sottospazi vettoriali

$$A = \{ \vec{a} \in R, \vec{b}=0 \}$$

$$B = \{ \vec{a} = 0, \vec{b} \in R \}$$

Il sottospazio A contiene i vettori sull'asse delle ascisse.

Il sottospazio B contiene i vettori sull'asse delle ordinate.

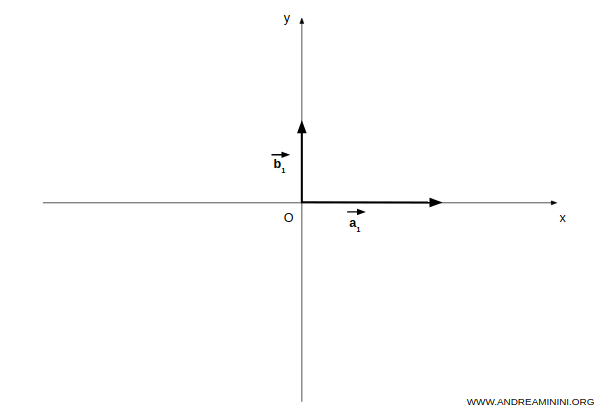
Ora considero il sottospazio composto dalla somma dei sottospazi vettoriali A+B

$$A+B$$

Il sottospazio somma A+B include al suo interno sia il sottospazio A che il sottospazio B.

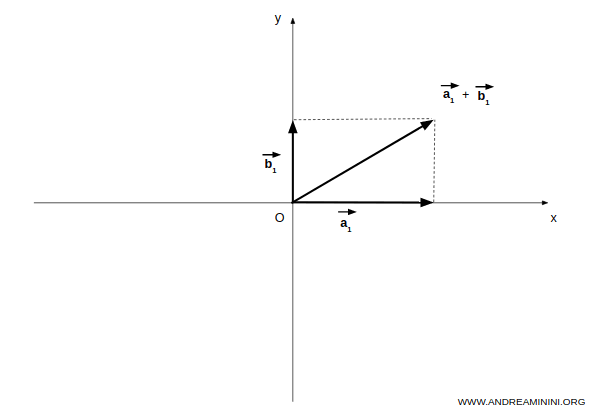
Inoltre, essendo un sottospazio include qualsiasi somma tra vettori e qualsiasi prodotto di un vettore per uno scalare ossia tutto il piano.

Il piu' piccolo sottospazio che contiene A e B

La somma degli spazi vettoriali A+B è il più piccolo sottospazio vettoriale di V che contiene l'unione dei sottospazi A∪B.

Dimostrazione

Considero un qualsiasi sottospazio vettoriale L che contiene tutti i vettori di A e B, ossia l'unione dei due sottospazi A∪B.

$$A \cup B \subseteq L$$

Pertanto, ogni vettore del sottospazio A è contenuto anche in L

$$\forall \ a \in A \rightarrow a \in L$$

Lo stesso vale per vettori di B

$$\forall \ b \in B \rightarrow b \in L$$

Essendo L un sottospazio vettoriale, per la definizione di sottospazio, contiene al suo interno anche la somma dei vettori di A e di B

$$\{ \vec{a}+\vec{b} \ | \ \vec{a} \in A \ , \ \vec{b} \in B \} \subseteq L$$

Quindi, il sottospazio vettoriale L contiene al suo interno il sottospazio vettoriale A+B

$$A+B \subseteq L$$

In generale, qualsiasi sottospazio vettoriale che contiene A e B include al suo interno anche la somma A+B.

Pertanto, fra tutti i sottospazi vettoriali che contengono l'unione dei sottospazi A∪B, il sottospazio somma A+B è il più piccolo.

Nota. Il sottospazio della somma dei sottospazi A+B è contenuto in tutti i sottospazi che contengono A e B. Di conseguenza A+B è sicuramente il più piccolo tra tutti i sottospazi che contengono A e B. Inoltre, qualsiasi sottoinsieme più piccolo Z di A+B che contenga A e B $$A, B \subset Z \subset A+B$$ non è un sottospazio perché non soddisfa una delle proprietà dei sottospazi vettoriali in quanto la somma dei vettori di A e B non è un'operazione interna in Z. Di conseguenza, A+B è il sottospazio più piccolo in grado di contenere i sottospazi A e B.

E così via