I sottospazi vettoriali
Cos'è un sottospazio vettoriale
Un sottospazio vettoriale è un sottoinsieme dello spazio vettoriale che soddisfa tutte le proprietà degli spazi vettoriali.
La definizione di sottospazio vettoriale
- Sia V uno spazio vettoriale su un campo K, un sottoinsieme è uno sottospazio vettoriale di V $$ W ⊆ V $$ se valgono le seguenti proprietà:
- Dati due elementi qualsiasi w1 e w2 di W, anche la loro somma w1+w2 appartiene all'insieme W $$ \forall \ \vec{w}_1 \ , \ \vec{w}_2 \ \in \ W \ \Rightarrow \ \vec{w}_1 + \vec{w}_2 \in W $$
- Dato uno scalare λ qualsiasi appartenente al campo K e un elemento qualsiasi w dell'insieme W, anche il prodotto λw appartiene all'insieme W. $$ \forall \ \lambda \in K \ , \ \forall \vec{w} \ \in \ W \ \Rightarrow \ \lambda \cdot \vec{w} \ \in \ W $$
In altri termini, un sottospazio vettoriale è un sottoinsieme chiuso alle operazioni di addizione e di prodotto per uno scalare.
A sua volta anche un sottospazio vettoriale è uno spazio vettoriale.
Quindi, in un sottospazio vettoriale valgono tutte le proprietà degli spazi vettoriali.
Nota. Quest'ultimo aspetto è molto importante perché non tutti i sottoinsiemi di uno spazio vettoriale sono anche sottospazi vettoriali. Per capire se un sottoinsieme è un sottospazio vettoriale oppure no devo verificare se soddisfa le proprietà degli spazi vettoriali.
Come verificare se un sottoinsieme è uno spazio vettoriale
Per capire se un sottoinsieme è anche uno spazio vettoriale, verifico se il sottoinsieme include l'elemento nullo oppure no.
A cosa serve?
L'elemento nullo è una delle proprietà degli spazi vettoriali.
Un sottospazio vettoriale è a sua volta uno spazio vettoriale. Quindi, deve contenere l'elemento nullo.
Se il sottoinsieme non ha un elemento nullo, il sottoinsieme non è un sottospazio vettoriale.
Una volta appurato che il sottoinsieme includa l'elemento nullo, verifico se rispetta le proprietà dei sottospazi vettoriali.
Un sottoinsieme è un sottospazio vettoriale se rispetta le due proprietà dei sottospazi vettoriali.
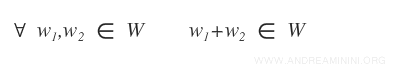
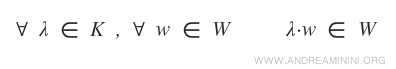
Quindi, calcolo la somma di due elementi del sottoinsieme e il prodotto scalare di due generici vettori del sottoinsieme W.
Se il risultato della somma e del prodotto scalare appartiene ancora al sottoinsieme W, allora il sottoinsieme è un sottospazio vettoriale. Altrimenti non lo è.
Un esempio pratico
Esempio 1
In questo semplice esempio verifico se un sottoinsieme W è un sottospazio vettoriale.

Esempio 2
In quest'altro esempio analizzo un altro sottoinsieme.
In questo caso l'equazione è uguale a uno e l'esito è completamente diverso.
![]()
Altri esempi svolti
Come riconoscere il sottospazio vettoriale tramite il grafico
Posso verificare le proprietà dei sottospazi vettoriali anche osservando la rappresentazione grafica sul piano cartesiano.
Se il sottoinsieme W contiene l'elemento nullo (0,0) il grafico passa per l'origine O.
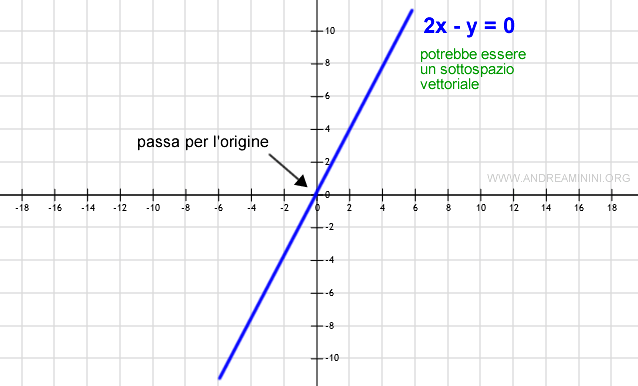
Nota. E' una condizione necessaria ma non sufficiente. Anche se la retta passa per l'origine non è detto che si tratti di un sottospazio vettoriale. Potrebbe esserlo oppure no.
Se invece il grafico non passa dall'origine, il sottoinsieme W non ha l'elemento nullo.
Quindi il sottoinsieme W non è un sottospazio vettoriale.
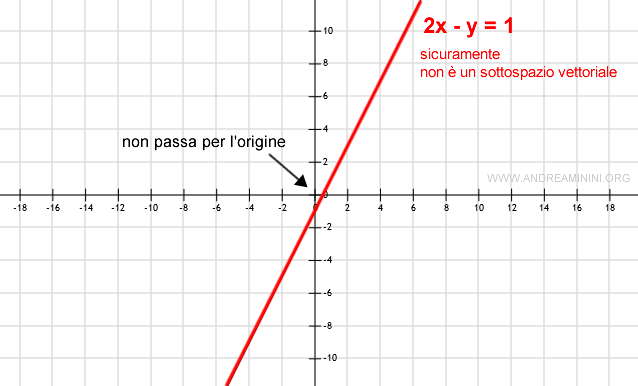
Nota. Se la retta non passa per l'origine è inutile qualsiasi altro controllo. Di sicuro il sottoinsieme W non è un sottospazio vettoriale.
Una volta appurato che la retta passa per l'origine, devo verificare se il sottoinsieme W rispetta le due proprietà dei sottospazi.
E' un sottospazio vettoriale se...
Il sottoinsieme W è un sottospazio vettoriale se la somma di due elementi qualsiasi è sempre un punto della retta ( insieme W ).
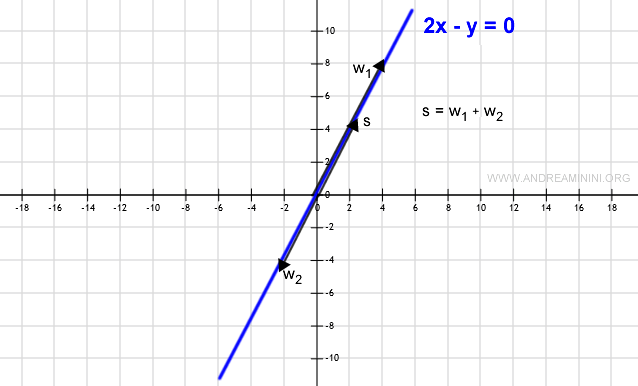
Inoltre, dato uno scalare e un elemento w qualsiasi, il prodotto scalare è sempre un vettore sulla retta ( insieme W ).
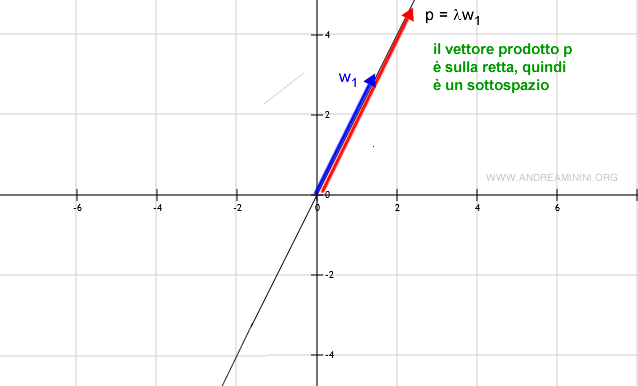
Non è un sottospazio vettoriale se...
Non è un sottospazio vettoriale se la somma w1+w2 determina un vettore al di fuori della retta ( insieme W ).
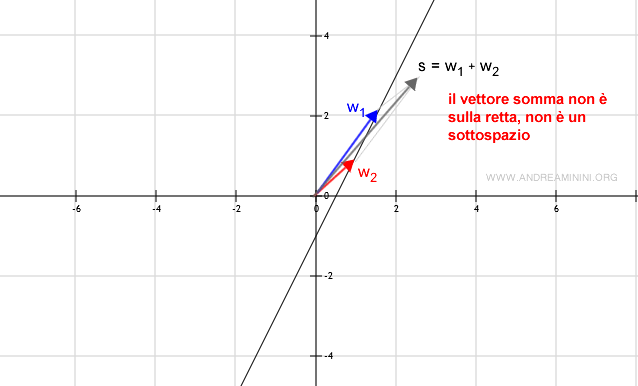
Oppure, dato un elemento w qualsiasi, il prodotto scalare λw determina un vettore al di fuori della retta ( sottoinsieme W ).
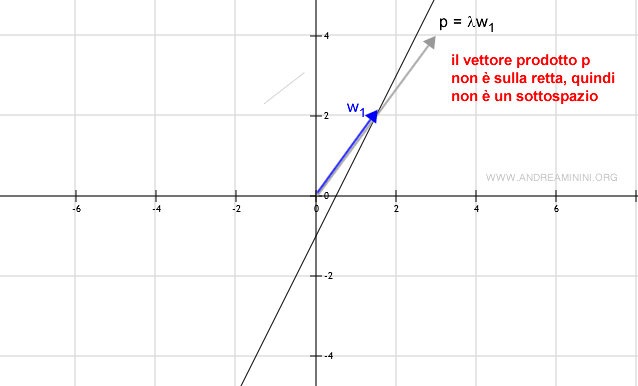
In conclusione, anche l'analisi grafica sul piano consente di scorgere le proprietà dei sottospazi vettoriali.
I sottospazi vettoriali e le combinazioni lineari
Un sottoinsieme W dello spazio vettoriale V è un sottospazio vettoriale di V se anche la sua combinazione lineare con n scalari appartiene a W.

Questa definizione riassume le due caratteristiche dei sottospazi vettoriali, ossia la chiusura rispetto alla somma e al prodotto scalare.
