Sottospazi supplementari
I sottospazi vettoriali sono detti sottospazi supplementari se sono in somma diretta e la loro somma è uguale all'intero spazio vettoriale.
La definizione di spazi supplementari
Dati due sottospazi A e B dello spazio vettoriale V, sono sottospazi supplementari se
$$ \begin{cases} A \oplus B \\ A + B = V \end{cases} $$
La prima proprietà ( somma diretta ) è un'intersezione banale.
$$A \oplus B => A \cap B = \{ 0_v \} $$
La seconda proprietà afferma che la somma dei sottospazi A+B è uguale all'intero spazio vettoriale V.
$$ A+B = V $$
Quando due sottospazi sono supplementari si scrive
$$A \oplus B = V $$
Per definire gli spazi supplementari devono essere soddisfatte entrambe le proprietà. Una sola delle due non è sufficiente.
La differenza tra somma diretta e somma di sottospazi. La somma diretta è l'insieme intersezione dei due sottospazi composto soltanto dal vettore nullo { 0v }. La somma di due sottospazi è, invece, l'insieme composto dalle somme dei loro elementi.
Esempi pratici
In questi esempi verifico se due sottospazi vettoriali sono supplementari oppure no.
Esempio 1
Dato uno spazio vettoriale V nel campo R3 e due sottospazi vettoriali A e B.
$$ A = \{ (x,y,z) \in R^3 ,\begin{cases} x=0 \\ y=0 \end{cases} \} $$
$$ B = \{ (x,y,z) \in R^3 , z=0 \} $$
Il sottospazio A è l'asse z ( blu ) nello spazio a 3 dimensioni.
Il sottospazio B, invece, è il piano (x,y) di colore rosso nello spazio a 3 dimensioni in corrispondenza di z=0.
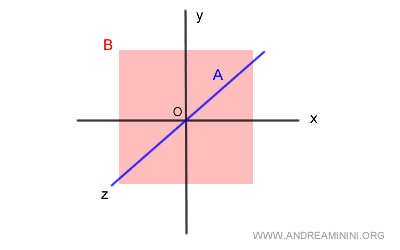
L'intersezione AVB è un insieme composto soltanto dal vettore nullo 0v ( intersezione banale ).
$$ A \cap B = \{0_v\} $$
Quindi i sottospazi A e B sono in somma diretta tra loro.
$$ A \oplus B $$
E' la prima condizione degli spazi vettoriali supplementari.
Ora devo verificare se la somma A+V è uguale allo spazio vettoriale V.
$$ A+B = V $$
La somma sposta il piano B in ogni punto dell'asse Z.
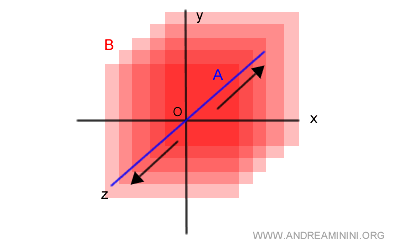
Pertanto, la somma A+B eguaglia lo spazio vettoriale V nel campo R3.
Anche la seconda condizione degli spazi supplementari è soddisfatta.
Quindi, i sottospazi A e B sono sottospazi supplementari.
Esempio 2
Dato uno spazio vettoriale V nel campo R3 e due sottospazi vettoriali A e B.
$$ A = \{ (x,y,z) \in R^3 ,\begin{cases} x=0 \\ y=0 \end{cases} \} $$
$$ B = \{ (x,y,z) \in R^3 ,\begin{cases} z=0 \\ y=0 \end{cases} \} $$
Il sottospazio A è l'asse z ( blu ) mentre il sottospazio B è l'asse x ( rosso ) nello spazio a 3 dimensioni.
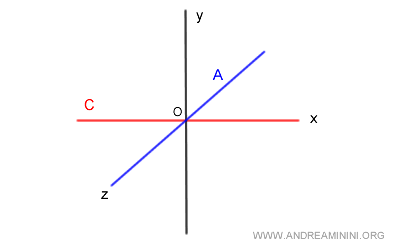
L'intersezione A⋂B è banale perché comprende soltanto il vettore nullo 0v.
$$ A \cap B = \{0_v\} $$
Quindi i sottospazi A e B sono in somma diretta tra loro.
$$ A \oplus B $$
Ora devo verificare se la loro somma A+B eguaglia lo spazio vettoriale V.
$$ A+B = \{ (x,y) \in R^2 \} $$
La somma A+B corrisponde al piano (x,z) su due dimensioni (R2).
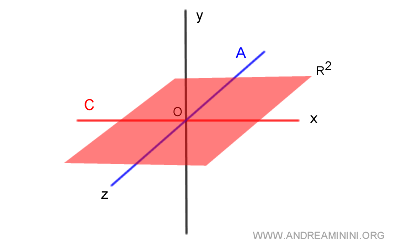
Non corrisponde allo spazio vettoriale V su tre dimensioni (R3).
Quindi, pur essendo in somma diretta tra loro, in questo caso i sottospazi A e B non sono sottospazi supplementari.
Esempio 3
Dato uno spazio vettoriale V nel campo R3, prendo due sottospazi vettoriali A e B.
$$ A = \{ (x,y,z) \in R^3 , \begin{cases} x=0 \\ y=0 \end{cases} \} $$
$$ C = \{ (x,y,z) \in R^3 , y=0 \} $$
Il sottospazio A è con l'asse z ( blu ) dello spazio a 3 dimensioni.
Il sottospazio C, invece, è il piano (x,z) dello spazio a 3 dimensioni in corrispondenza di y=0 ( piano rosso ).
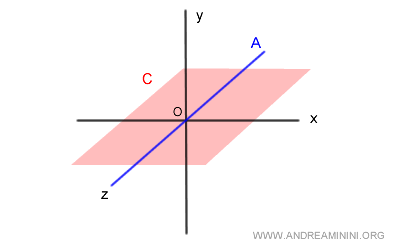
Calcolo l'intersezione tra A e C
$$ A \cap C=\{ R \} <> \{ 0_v \}$$
L'insieme intersezione A⋂B è composto dagli infiniti punti dell'asse Z ( blu ). E' diverso da { 0v }.
Pertanto, in questo caso i sottospazi A e C non sono in somma diretta tra loro.
Non essendo in somma diretta, i sottospazi A+V non sono sottospazi supplementari.
E' quindi inutile verificare se la somma A+C sia uguale a V.
E così via.
