Lo spazio vettoriale dei vettori geometrici applicati
Uno spazio vettoriale dei vettori geometrici del piano applicati al punto O, è l'insieme dei vettori che hanno origine nel punto O e terminano in qualsiasi altro punto del piano.
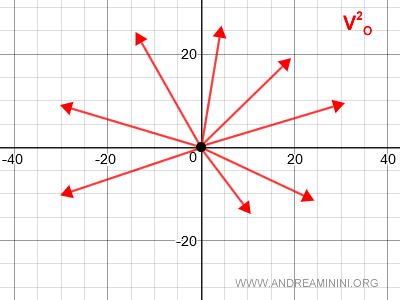
Spiegazione
Dato un punto O del piano, l'insieme dei vettori applicati in O è uno spazio vettoriale V2O.
Cos'è un vettore applicato in O? E' un vettore OP che ha origine in O e termina nel punto P.
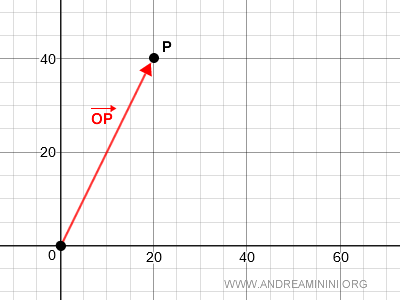
Nello spazio vettoriale V2O si possono calcolare le operazioni di addizione e prodotto per uno scalare.
Addizione tra vettori
Dati due vettori OP e OQ, l'addizione dei vettori è la seguente:
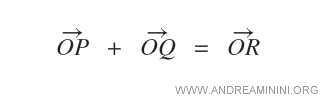
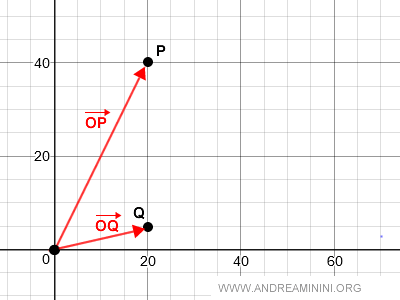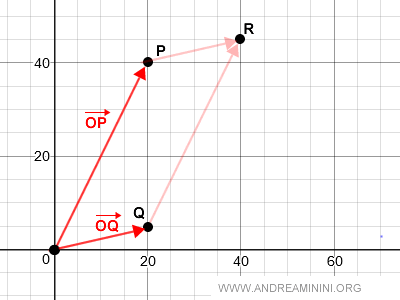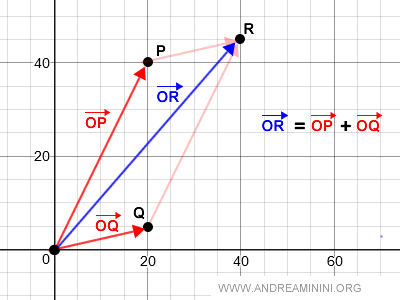
Secondo la regola del parallelogramma, l'addizione dei vettori è la diagonale del parallelogramma OPRQ.
Dal punto di vista grafico l'addizione di due vettori geometrici è la seguente:
Prodotto di un vettore per uno scalare
Dato un vettore OP e un numero scalare α, il prodotto è un vettore OQ che ha origine nel punto O e termina nel punto Q.
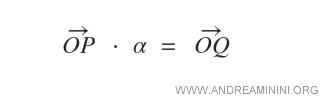
Il coefficiente angolare del vettore OQ è il seguente:
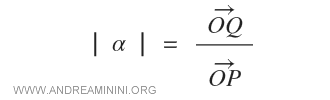
La rappresentazione su due dimensioni del prodotto di un vettore per uno scalare è la seguente:
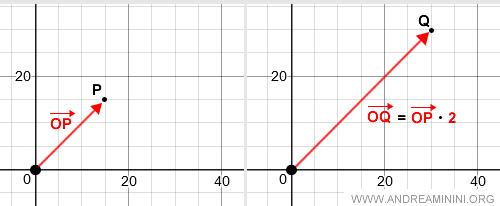
A seconda del segno di α, il vettore OQ si aggiunge in un verso o nell'altro del vettore OP.
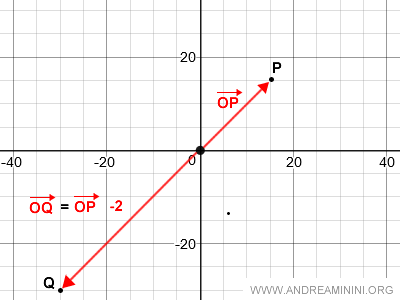
La direzione dei vettori OQ e OP è sempre la stessa, perché il valore assoluto del coefficiente angolare |α| è lo stesso.
Alcuni casi particolari
Se lo scalare α è uguale a uno (α=1), il prodotto OQ è uguale al vettore OP.
Se lo scalare α è uguale a meno uno (α=-1), il prodotto OQ è uguale al vettore opposto OP', dove il punto P' è il simmetrico di P rispetto a O.
Se lo scalare α è nullo (α=0), il prodotto di OP per lo scalare è il punto OO ossia è un vettore nullo OO.
