Generatori dello spazio vettoriale
Un sistema di generatori è un insieme di vettori S={v1,...,vm} di uno spazio vettoriale V $$ S = \{ v_1 , ... , v_m \} \in \ V $$ che permette di determinare ogni vettore vi∈V dello spazio vettoriale tramite la combinazione lineare dei vettori di S con altrettanti a1,...am ∈ R coefficienti scalari $$ \vec{v}_i=a_1 \vec{v}_1 +...+ a_m \vec{v}_m \ \ \ \forall v_i \in V $$
In pratica, le combinazioni lineari dei vettori S={v1,...,vm} generano tutti i vettori dello spazio vettoriale V.
Per questo i vettori di S sono detti generatori.
Pertanto, dato un insieme S di vettori dello spazio vettoriale V
$$ S = \{ v_1, v_2, ... ,v_n \} $$
Il più piccolo sottospazio vettoriale lineare L(S) che contiene S è uguale allo spazio vettoriale V.
$$ L(S) = V $$
Il numero dei vettori generatori in S può essere finito o infinito, purché sempre inferiore o uguale al numero dei vettori dello spazio vettoriale V.
$$ m \le i $$
In questi appunti indico l'insieme dei vettori generatori con S e il sottospazio vettoriale di S con L(S).
A cosa serve un generatore di spazio vettoriale
Uno spazio vettoriale V può essere composto da infiniti vettori. Per descriverlo non è però necessario elencarli tutti.
Ogni vettore v ∈ V posso scriverlo come combinazione lineare di altri vettori dello spazio vettoriale.
Esempio
$$ v_4 = a_1 v_1 + a_2 v_2 + a_3 v_3 $$ $$ v_5 = a_1 v_1 + a_2 v_2 + a_3 v_3 $$ $$ v_6 = a_1 v_1 + a_2 v_2 + a_3 v_3 $$ $$ \vdots $$
Basta scegliere opportunamente un sottoinsieme finito o infinito di vettori S={v1,..,vm}.
$$ L = \{ v_1 , v_2 , v_3 \} $$
Dalla combinazione lineare dei vettori di S con m numeri scalari αm posso ottenere qualsiasi altro vettore dello spazio vettoriale V.
$$ \forall \ v_i \in V \: \: v = a_1 v_1 + a_2 v_2 + a_3 v_3 $$
Un esempio di generatore
L'intero spazio vettoriale V = R2 nel campo dei numeri reali R può essere generato da due soli vettori.
$$ v_1 = ( 1, 0 ) $$ $$ v_2 = ( 0, 1 ) $$
Questi due vettori sul piano cartesiano R2 sono così rappresentati:
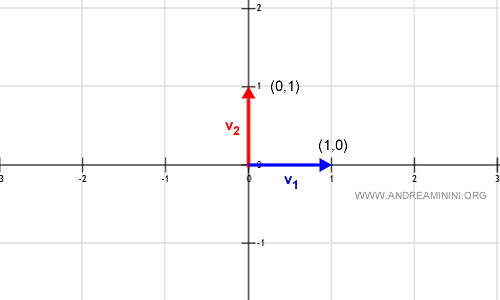
Per dimostrare che i vettori v1 e v2 siano generatori dello spazio vettoriale R2, scrivo la loro combinazione lineare con due scalari a1 e a2 appartenenti a R.
$$ v = a_1 v_1 + a_2 v_2 \: \: \: \: \: \: con \: \: a_1=1 , a_2=1 $$
$$ v = 1 ( 1 , 0 ) + 1 ( 0 , 1 ) = $$
$$ v = ( 1 , 0 ) + ( 0 , 1 ) $$
$$ v = ( 1 , 1 ) $$
Questa combinazione lineare genera un altro vettore (v3) dello spazio vettoriale V che punta alle coordinate (1,1).
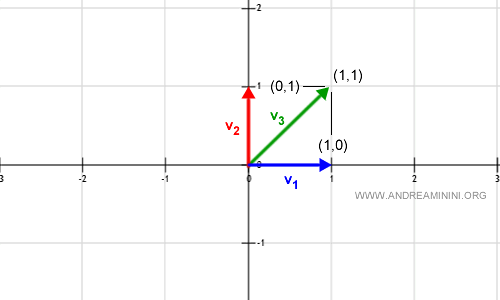
Ora modifico la combinazione lineare usando lo scalare a2=2.
$$ v = a_1 v_1 + a_2 v_2 \: \: \: \: \: \: con \: \: a_1=1 , a_2=2 $$
$$ v = 1 ( 1 , 0 ) + 2 ( 0 , 1 ) = $$
$$ v = ( 1 , 0 ) + ( 0 , 2 ) $$
$$ v = ( 1 , 2 ) $$
Il vettore v2 ha raddoppiato la lunghezza mentre v1 è rimasto tale e quale.
Questa combinazione lineare genera un altro vettore (v4) dello spazio vettoriale, diverso dal precedente, che punta alle coordinate (1,2).
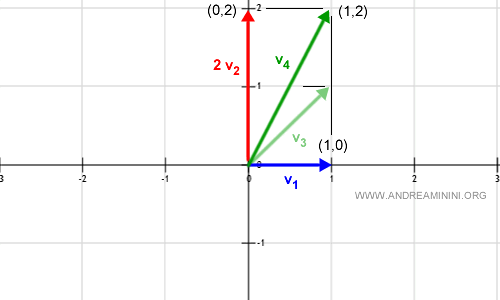
In questo modo, modificando gli scalari a1 e a2 dei vettori v1 e v2 posso generare ogni vettore v dello spazio vettoriale V.
Pertanto, posso affermare che v1 e v2 sono un sistema di generatori dello spazio vettoriale R2.
$$ L_R = \{ v_1 , v_2 \} = R^2$$
E così via.
Nota. Il solo vettore v1 non è invece un generatore dello spazio vettoriale V=R2 perché genera soltanto i vettori sulla retta delle ascisse (x). E' quindi soltanto un generatore del sottospazio {x}. Lo stesso si può dire per il vettore v2, preso singolarmente non è un generatore di R2 perché genera vettori solo sulla retta delle ordinate. E' quindi soltanto un generatore del sottospazio {y}.
Esempio 2
Un generatore dello spazio vettoriale può essere composto anche da un solo vettore.
Ad esempio, in uno spazio vettoriale V nel campo K=R dei numeri reali, considero un vettore v qualsiasi non nullo.
$$ \vec{v} \in V $$
Dal punto di vista grafico
Il vettore v deve essere non nullo.
$$ \vec{v} \in \vec{0} $$
L'insieme generato dal vettore L(v) è composto dalla combinazione lineare del vettore v con gli scalari k di K
$$ L(v) = \{ k \cdot \vec{v} \} $$
I vettori generati hanno la stessa direzione del vettore generatore, ossia si si trovano sulla stessa retta.
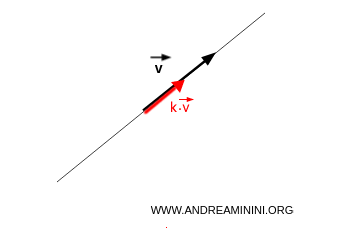
Quello che cambia è il verso e il modulo (lunghezza) di ciascun vettore.
Nota. Il vettore generatore deve essere non nullo, perché qualsiasi scalare moltiplicato per un modulo pari a zero è sempre zero.
Esempio 3
In generale due vettori v1, v2 non nulli generano un sottospazio vettoriale
$$ \vec{v_1} \ne 0 $$ $$ \vec{v_2} \ne 0 $$
Il sottospazio generato dipende dalla dipendenza o indipendenza lineare tra i due vettori.
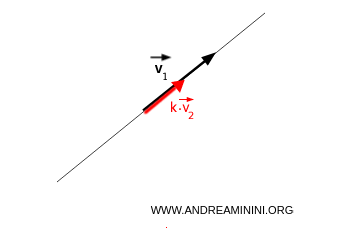
- Se i due vettori sono paralleli $$ \vec{v_1} = k \cdot \vec{v_2} $$ allora il sottospazio vettoriale generato dai due vettori L(v1,v2) si trova sulla rette che contiene i due vettori v1, v2
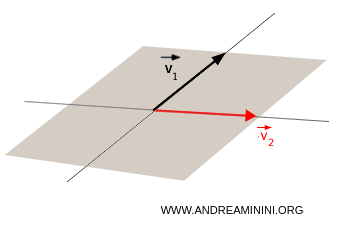
- Se i vettori non sono paralleli $$ \vec{v_1} \ne k \cdot \vec{v_2} $$ allora il sottospazio vettoriale generato dai due vettori è il piano che contiene i due vettori v1 e v2.
Come verificare se i vettori sono generatori
Per verificare se i vettori sono un sistema di generatori dello spazio vettoriale V, devo risolvere il sistema di equazioni della loro combinazione lineare.
Un esempio pratico
Ho due vettori v1=(1,0) e v2=(2,1) nello spazio vettoriale V=R2.
$$ v_1 = (1,1) $$ $$ v_2 = (2,1) $$
Devo capire se sono generatori dello spazio vettoriale V.
La combinazione lineare dei due vettori v1 e v2 è la seguente:
$$ a_1 v_1 + a_2 v_2 $$
$$ a_1 (1,1) + a_2 (2,1) $$
$$ ( a_1 , a_1 ) + (2 a_2 , a_2 ) $$
$$ ( a_1 + 2 a_2 , a_1 + a_2 ) $$
Queste ultime due sono le coordinate di destinazione (x,y) del vettore generato dalla combinazione lineare dei due vettori.
$$ (x,y) = ( a_1 + 2 a_2 , a_1 + a_2 ) $$
Posso riscrivere l'uguaglianza vettoriale sotto forma di sistema di equazioni
$$ \begin{cases} a_1 + 2 a_2 = x \\ a_1 + a_2 = y \end{cases}$$
Se il sistema ammette soluzioni nelle incognite a1 e a2 per ogni possibile valore (x,y), allora i due vettori v1 e v2 sono generatori dello spazio vettoriale V=R2.
Viceversa, se non ammette soluzioni, i due vettori v1 e v2 non sono generatori dello spazio vettoriale V=R2.
Nota. Per dimostrare che il sistema ha delle soluzioni ( una o infinite ) mi basta applicare il teorema di Rouché-Capelli, secondo il quale un sistema di equazioni lineari ha soluzioni se il rango della matrice dei coefficienti A è uguale al rango della matrice completa A|B. In tale caso il sistema ha ∞n-r soluzioni dove r è il rango e n è il numero delle variabili incognite.

In questo caso il sistema ammette soluzioni.
E' pertanto un generatore dello spazio vettoriale V.
Verifica
Come ulteriore verifica svolgo i calcoli per trovare la soluzione del sistema.
$$ \begin{cases} a_1 + 2 a_2 = x \\ a_1 = y - a_2 \end{cases}$$
$$ \begin{cases} y - a_2 + 2 a_2 = x \\ a_1 = y - a_2 \end{cases}$$
$$ \begin{cases} y + a_2 = x \\ a_1 = y - a_2 \end{cases}$$
$$ \begin{cases} a_2 = x - y \\ a_1 = y - a_2 \end{cases}$$
$$ \begin{cases} a_2 = x - y \\ a_1 = y - (x-y) \end{cases}$$
$$ \begin{cases} a_2 = x - y \\ a_1 = 2y - x \end{cases}$$
Il sistema è risolto per qualsiasi combinazione di valori di x e y, ossia su tutti i punti del piano cartesiano.
Pertanto, v1 e v2 sono generatori dello spazio vettoriale R2.
Differenza tra sistema di generatori e span lineare
Uno span lineare è un insieme di vettori Sp dello spazio vettoriale V
$$ S_p = \{ v_1,.v_2, ...,v_m \} $$
la cui combinazione lineare è un vettore che appartiene a V.
$$ a_1 v_1 + ... + a_m v_m \in V $$
Ogni combinazione lineare dei vettori dello span Sp appartiene allo spazio vettoriale V.
$$ L(S_p) \subseteq a V $$
Non è però detto che ogni vettore dello spazio vettoriale V sia ottenibile da una combinazione lineare dell'insieme span Sp.
$$ L(S_p) \ne a V $$
Nota. I vettori dello span {v1,...,vn} sono sicuramente dei generatori per un sottospazio L(Sp). Non è detto che lo siano per l'intero spazio vettoriale V.
Viceversa, un sistema di generatori è un insieme S di vettori
$$ S = \{ v_1,.v_2, ...,v_n \} $$
la cui combinazione lineare genera tutti i vettori dello spazio vettoriale V.
$$ L(S) = V $$
Pertanto, un insieme di vettori che forma uno span non è che detto che sia anche un insieme di generatori.
$$ L(S_p) \ne L(S) = V $$
Come ridurre l'insieme di generatori
Un insieme di vettori {v1,...,vm} è un sistema di generatori ma non è detto che sia anche l'insieme più piccolo possibile di generatori dello spazio vettoriale V.
Infatti, dato un sistema di generatori
$$ v = a_1 v_1 + ... + a_m v_m $$
Se aggiungessi un ulteriore vettore vm+1 con uno scalare am+1 = 0, otterrei un altro sistema generatore dello stesso spazio vettoriale V.
$$ v= a_1 v_1 + ... + a_m v_m + a_{m+1} v_{m+1} $$
$$ con \:\:\: a_{m+1} = 0 $$
Pertanto, anche se un insieme di vettori è un sistema di generatori dello spazio vettoriale, potrebbe essere ulteriormente ridotto.
Esempio

Come si riduce un sistema di generatori?
Per ridurre un sistema di generatori bisogna eliminare i vettori linearmente dipendenti dagli altri .
Dimostrazione
In un sistema di generatori il vettore vm è linearmente dipendente dagli altri.
$$ v = a_1 v_1 + ... + a_m v_m $$
Quindi, posso riscrivere vm come combinazione lineare degli altri.
$$ v = β _1 v_1 + ... + β _{m-1} v_{m-1} $$
Sostituendo la combinazione lineare nel sistema di generatori
$$ v = a_1 v_1 + ... + a_m ( β _1 v_1 + ... + β _{m-1} v_{m-1} ) $$
$$ v = a_1 v_1 + ... + a_m β _1 v_1 + ... + a_m β _{m-1} v_{m-1} ) $$
$$ v = v_1 ( a_1 + a_m β _1 ) + ... + v_{m-1} ( a_{m-1} + a_m β _{m-1} ) $$
I coefficienti (a1+amβ1 ) ... (am-1+amβm-1 ) sono comunque numeri scalari del campo R.
Quindi posso riscriverli come γ1 , ... , γm-1 ∈ R
$$ v = γ _1 v_1 + ... + γ _{m-1} v_{m-1} $$
Il che dimostra che anche { v1, v2 } è un sistema di generatori dello spazio vettoriale V.
E così via.
Esempio

Differenza tra sistema di generatori e base
Un sistema di generatori è detto base dello spazio vettoriale V se i vettori dell'insieme S $$ S = \{ v_1, v_2, ... , v_n \} $$ sono vettori linearmente indipendenti
Una base è detta anche sistema libero di generatori
Le combinazioni lineari dei vettori dell'insieme S={v1,v2,..,vn} generano tutti i vettori dello spazio vettoriale V
$$ \vec{v}_i=a_1 \vec{v}_1 +...+ a_m \vec{v}_n \ \ \ \forall \ v_i \in V $$
Lo stesso accade nei sistemi di generatori.
Tuttavia, nel caso delle basi, ogni vettore dello spazio vettoriale V è generato da una e una sola combinazione lineare dei vettori dell'insieme S.
Nota. Viceversa, in un sistema di generatori con vettori linearmente dipendenti ogni vettore dello spazio vettoriale V può essere composto da infinite combinazioni dei vettori dell'insieme S.
In questi casi il sistema di generatori è detto base dello spazio vettoriale.
