Campo

Cos'è un campo

Un campo K è una struttura algebrica composta da insieme non vuoto e due operazioni binarie + e · che soddisfano le seguenti proprietà.

• Proprietà associativa
  $$ (a+b) + c = a+(b+c) \ \ \ \ \ \ a,b,c \in K $$ $$ (a·b)·c = a·(b·c) \ \ \ \ \ \ \ \ \ \ \ \ \ \ a,b,c \in K $$
• Proprietà commutativa
  $$ a+b = b+a \ \ \ \ \ \ \ \ a,b \in K $$ $$ a·b = b·a \ \ \ \ \ \ \ \ \ \ \ \ a,b \in K $$
• Esistenza elemento neutro dell'addizione
  Esiste almeno un elemento 0 di K tale che
  $$ 0+a=a+0=a \ \ \ \ \ \forall a \in K $$
• Esistenza elemento neutro del prodotto
  Esiste un elemento 1 di K tale che $$ 1·a=a·1=a \ \ \ \ \forall \ a \in K $$
• Esistenza elemento opposto
  Per ogni elemento a appartenente K esiste un elemento -a di K tale che
  $$ a +(-a)=0 \ \ \ \ \ \forall \ a \in K $$
• Esistenza elemento inverso
  Per ogni a≠0 esiste un elemento inverso a^-1 (o 1/a) tale che $$ a \cdot a^{-1}=a^{-1} \cdot a=1 \ \ \ \ \ \ \ \ \forall \ a \in K - \{ 0 \} $$
• Proprietà distributiva
  $$ (a+b)·c=(a·c)+(b·c) \ \ \ \ \ \ \ \ \ \ \ \ \ \ a,b,c \in K $$ $$ c·(a+b)=(c·a)+(c·b) \ \ \ \ \ \ \ \ \ \ \ \ \ \ a,b,c \in K $$

Se le operazioni rispettano queste proprietà, l'insieme K è un campo (K,+, ·).

Nota. Le operazioni di un campo non necessariamente devono essere l'addizione e la moltiplicazione. Possono anche essere altre, purché rispettino le proprietà precedenti. Anche i simboli (+,·) possono essere diversi.

 

Campi infiniti e finiti

I campi sono classificati in

• Campi infiniti
  se il campo è un insieme composto da infiniti elementi.
• Campi finiti
  se il campo è un insieme composto da un numero finito di elementi.

Pertanto, non necessariamente un campo deve avere infiniti elementi.

Esempio di campo numerico

Ecco alcuni esempi di campi

Esempio 1

Un esempio di campo infinito è il campo dei numeri reali (R,+,·).

$$ (R, \ +, \ ·) $$

L'insieme dei numeri reali R con le operazioni di addizione e moltiplicazione è un campo, perché le operazioni di addizione e moltiplicazione soddisfano tutte le proprietà dei campi.

Ad esempio, presi due elementi qualsiasi dall'insieme dei numeri reali, la somma e il prodotto sono anch'essi numeri reali.

Esempio 2

L'insieme dei numeri interi Z con le operazioni di addizione e moltiplicazione non è un campo

$$ (Z, \ +, \ ·) $$

Non è un campo perché soltanto i numeri interi +1 e -1 hanno un elemento inverso.

Tutti gli altri numeri interi non hanno un elemento inverso.

Ad esempio, nell'insieme dei numeri interi Z non esiste il numero intero inverso 1/2 (o 2^-1) di +2.

Esempio 3

Un esempio di campo finito è il campo ({0,1},+,·).

In questo caso l'insieme {0,1} è un insieme finito ed è composto da due soli elementi.

$$ K = \{ 0,1 \} $$

Ogni operazione ha per risultato un elemento dell'insieme K

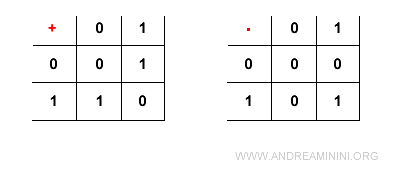
La somma e il prodotto soddisfano comunque tutte le proprietà di un campo.

Ad esempio, lo zero (0) è l'elemento neutro dell'addizione mentre uno (1) è l'elemento neutro del prodotto.

L'elemento opposto di 0 è 0, l'elemento opposto di 1 è 1.

Nota. Nel caso 1+1 potevo scegliere come risultat 1+1=0 oppure 1+1=1. Tuttavia, se scegliessi quest'ultimo 1+1=1, considerando che 1+0=1 e 0+1=1, l'elemento 1 non avrebbe un numero opposto. Pertanto, sarebbe violata una proprietà dei campi. Viceversa, 1+1=0 consente all'elemento 1 di avere come opposto se stesso.

L'elemento inverso di 1 è 1 perché 1·1=1.

Lo zero, invece, non deve avere inversi perché la proprietà di esistenza dell'inverso vale solo per gli elementi diversi dallo zero (elemento neutro).

Inoltre, tutte le altre proprietà dei campi sono soddisfatte

Ecco alcuni esempi

• Proprietà associativa
  $$ (0+1) + 1 = 0+(1+1) $$ $$ (0·1)·1 = 0·(1·1) $$
• Proprietà commutativa
  $$ 0+1 = 1+0 $$ $$ 0·1 = 1·0 $$
• Proprietà distributiva
  $$ (0+1)·1=(0·1)+(1·1) $$ $$ 1·(0+1)=(1·0)+(1·1) $$

Esempio 4

Non tutti gli insiemi finiti sono anche campi.

Ad esempio un insieme composto da 4 elementi non è un campo.

$$ K = \{ 0,1, 2, 3 \} $$

Per costruire le operazioni utilizzo la tecnica dell'orologio dell'aritmetica modulare.

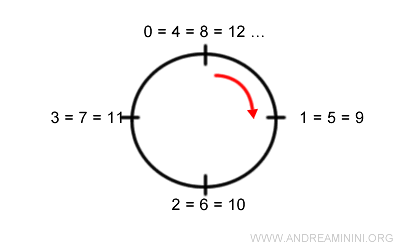
In questo modo costruisco le due tabelle delle operazioni di addizione e moltiplicazione.

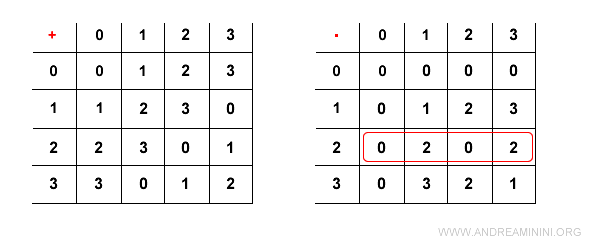
Questo insieme non è un campo perché non rispetta una proprietà dei campi.

Il simbolo 2 non ha l'elemento neutro (1) della moltiplicazione.

Nota. Generalmente un insieme composto da K elementi è un campo se K è un numero primo (es. 2, 3, 5, 7, ecc. )

E così via.