Esercizi sugli spazi vettoriali
Alcuni esercizi svolti sugli spazi vettoriali
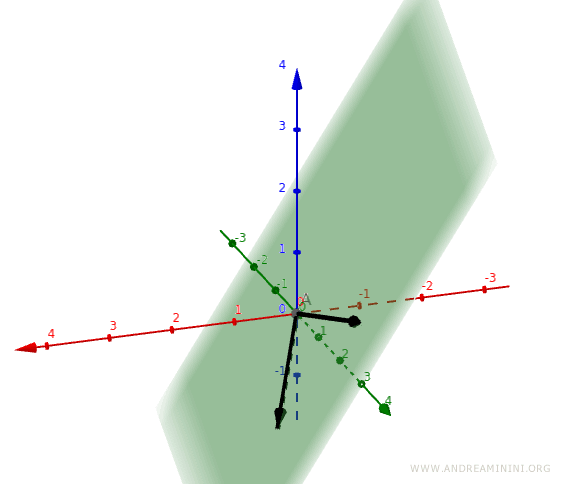
Esercizio 1
Considero due vettori nello spazio vettoriale V=R3
$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} $$
$$ v_2 = \begin{pmatrix} 0 \\ 3 \\ 1 \end{pmatrix} $$
I due vettori sono generatori di R3?
Devo verificare se posso scrivere un generico vettore v di R3
$$ v = \begin{pmatrix} a \\ b \\ c \end{pmatrix} \ \in V = R^3 $$
come combinazione lineare dei vettori v1 e v2
$$ \vec{v} = \lambda_1 \cdot \vec{v}_1 + \lambda_2 \cdot \vec{v}_2 $$
$$ \begin{pmatrix} a \\ b \\ c \end{pmatrix} = \lambda_1 \cdot \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} + \lambda_2 \cdot \begin{pmatrix} 0 \\ 3 \\ 1 \end{pmatrix} $$
Trasformo l'equazione vettoriale in un sistema di tre equazioni e due incognite.
$$ \begin{cases} \lambda_1 + 0 = a \\ 2 \lambda_1 + 3 \lambda_2 = b \\ - \lambda_1 + \lambda_2 = c \end{cases} $$
$$ \begin{cases} \lambda_1 = a \\ 2 \lambda_1 + 3 \lambda_2 = b \\ - \lambda_1 + \lambda_2 = c \end{cases} $$
$$ \begin{cases} \lambda_1 = a \\ 2 a + 3 \lambda_2 = b \\ - a + \lambda_2 = c \end{cases} $$
$$ \begin{cases} \lambda_1 = a \\ 2 a + 3 \lambda_2 = b \\ \lambda_2 = c+a \end{cases} $$
$$ \begin{cases} \lambda_1 = a \\ 2 a + 3 (c+a) = b \\ \lambda_2 = c+a \end{cases} $$
$$ \begin{cases} \lambda_1 = a \\ 2 a + 3c + 3a = b \\ \lambda_2 = c+a \end{cases} $$
$$ \begin{cases} \lambda_1 = a \\ 5 a + 3c = b \\ \lambda_2 = c+a \end{cases} $$
Il sistema di equazioni ha soluzioni soltanto se 5a+3c=b
Quindi, non ha soluzioni per qualsiasi valore di a, b, c.
Questo vuol dire che i due vettori v1 e v2 non possono generare tutti i vettori v(a,b,c) dello spazio vettoriale V=R3
Pertanto, i due vettori v1 e v2 non sono generatori dello spazio vettoriale V=R3
Nota. Del resto due vettori linearmente indipendenti come v1 e v2 possono generare solo tutti i vettori del piano R2 in cui risiedono. In questo caso lo spazio vettoriale è di dimensioni più grandi R3. Due soli vettori non possono generare tutti i vettori di uno spazio a tre dimensioni. Per riuscirci servono almeno tre vettori linearmente indipendenti.
Esercizio 2
Dato lo spazio vettoriale M(2,2,R) delle matrici quadrate di ordine 2, il sottoinsieme A di M(2,2,R) composto dalle matrici $$ \begin{pmatrix} a & b \\ c & 1 \end{pmatrix} \ \ \ \ a,b,c \in R $$ è un sottospazio vettoriale di M(2,2,R)?
Per rispondere alla domanda verifico se il sottoinsieme A soddisfa le proprietà degli spazi vettoriali e le proprietà dei sottospazi vettoriali.
1] Verifico se il sottoinsieme A è un spazio vettoriale
E' sicuramente un sottoinsieme non vuoto.
Tuttavia, è evidente fin dall'inizio che il sottoinsieme non contiene al suo interno la matrice quadrata nulla, ossia la matrice composta solo da zeri.
$$ \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \ \ \notin \ A $$
La presenza dell'elemento nullo rispetto all'addizione è una delle condizioni dello spazio vettoriale.
Pertanto, il sottoinsieme A non è un spazio vettoriale. Quindi, il sottoinsieme A non è un sottospazio vettoriale di M(2,2,R).
Nota. Questo esercizio dimostra la convenienza a verificare prima le condizioni più facili. Ad esempio, la presenza dell'elemento neutro dell'addizione o della moltiplicazione. Poi tutte le altre. Questa accortezza fa risparmiare molto tempo.
Esercizio 3
Dato lo spazio vettoriale M(2,2,R) composto dalle matrici quadrate di ordine 2, verificare se il sottoinsieme A di M(2,2,R) composto dalle matrici $$ \begin{pmatrix} a & b \\ c & b-1 \end{pmatrix} \ \ \ \ a,b,c \in R $$ è un sottospazio vettoriale di M(2,2,R)?
Per prima cosa verifico se il sottoinsieme A soddisfa le proprietà degli spazi vettoriali.
Poi verifico se soddisfa anche le proprietà dei sottospazi vettoriali.
1] Il sottoinsieme A è un spazio vettoriale?
L'insieme A delle matrici quadrate M(2,2,R) è sicuramente un sottoinsieme non vuoto.
Tuttavia, è subito evidente che il sottoinsieme A non può contenere la matrice quadrata nulla, ossia la matrice composta solo da zeri
$$ \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \ \ \notin \ A $$
perché due elementi della matrice usano lo stesso parametro. Si tratta di b e b-1
$$ \begin{pmatrix} a & \color{red}b \\ c & \color{red}{b-1} \end{pmatrix} \ \ \ \ a,b,c \in R $$
Ad esempio, se scelgo a=0, b=0, c=0 non ottengo la matrice nulla
$$ \begin{pmatrix} 0 & 0 \\ 0 & \color{red}{-1} \end{pmatrix} \ \ \ \ a,b,c \in R $$
Allo stesso modo, se scelgo la combinazione a=0, b=1, c=0 non ottengo la matrice nulla
$$ \begin{pmatrix} 0 & \color{red}{1} \\ 0 & 0 \end{pmatrix} \ \ \ \ a,b,c \in R $$
Sapendo che la presenza dell'elemento nullo rispetto all'addizione è una delle condizioni dello spazio vettoriale, posso concludere che l'insieme A non è uno spazio vettoriale.
Pertanto, il sottoinsieme A non può essere un sottospazio vettoriale di M(2,2,R).
E così via.
