Sottospazio vettoriale generato da un insieme di vettori

Il sottospazio vettoriale generato da un insieme S di vettori dello spazio vettoriale V $$ S = \{ v_1 , v_2, ... , v_n \} $$ è il più piccolo sottospazio vettoriale di V che contiene S. Si indica con L(S) o <S>. $$ L(S) \ \ \ oppure \ \ \ <S> $$ Dove L significa lineare.

L'insieme di vettori S non è un sottospazio.

$$ S = \{ v_1 , v_2, ... , v_n \} $$

Il sottospazio L(S) è composto da tutte le combinazioni vettoriali dell'insieme S

$$ L(S) = \{ \lambda_1 v_1 + \lambda_2 v_2 + ... + \lambda_n v_n \ | \ v_i \in S \ , \ \lambda_i \in K \} $$

La spiegazione

Considero uno spazio vettoriale V.

Prendo un insieme S di vettori dello spazio vettoriale V.

$$ S = \{ v_1 , v_2, ... , v_n \} \subset V $$

Per ipotesi l'insieme S non è uno spazio vettoriale. E' soltanto un insieme composto da 2 o più vettori.

Il sottospazio vettoriale più piccolo di V che contiene l'insieme S è detto sottospazio vettoriale generato dall'insieme S dei vettori e si indica con il simbolo L(S) o <S>

$$ L(S) \ \ \ oppure \ \ \ <S> $$

Il sottospazio vettoriale L(S) è composto dalla combinazione lineare degli n vettori di S con altrettanti n scalari k.

$$ L(S) = \{ k_1 \vec{v}_1 + k_2 \vec{v}_2 + ... + k_n \vec{v}_n \ \ | \ \ v_i \in S \ . \ k_i \in K \} $$

che posso indicare anche con una sommatoria

$$ L(S) =\{ \sum_{i=1}^n k_i \ , \ \vec{v}_i \in S \} $$

Il sottospazio vettoriale L(S) è composto da m≥n vettori ottenuti dalla combinazione lineare degli n vettori dell'insieme S.

Sottospazio generato da un vettore

Considero un solo vettore non nullo dello spazio vettoriale

$$ \vec{v} \in V \ , \ \vec{v} \ne 0 $$

Quindi l'insieme S è composto da un solo vettore

$$ S = \{ \vec{v} \} \subset V $$

Dal punto di vista geometrico il vettore si trova su una retta.

In questo caso il sottospazio generato da S è l'insieme L(S) dei vettori ottenuti dalla combinazione lineare di un solo vettore per uno scalare

$$ L(\vec{v}) = \{ \lambda \vec{v} \ | \ \forall \ \lambda \in K \} $$

Il sottospazio vettoriale è composto da tutti i vettori che si trovano sulla stessa retta.

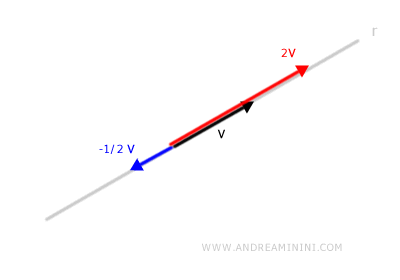
I vettori del sottospazio hanno tutti la stessa direzione.

Possono però variare in lunghezza e verso.

Nota. Nel caso particolare in cui il vettore è un vettore nullo, il sottospazio vettoriale generato dal vettore nullo è composto soltanto dal vettore nullo. $$ L(\vec{0}) = \{ \vec{0} \} $$ perché il prodotto tra uno scalare e il vettore nullo è sempre il vettore nullo.

Sottospazio generato da due vettori

Il sottospazio generato da due vettori v₁, v₂ non nulli dello spazio vettoriale V nel campo K

$$ v_1, v_2 \in V \ , \ v_1,v_2 \ne \vec{0} $$

dipende dalla dipendenza lineare o meno dei due vettori

• Se i due vettori sono paralleli
  In questo caso i due vettori sono linearmente dipendenti. Posso scrivere un vettore come multiplo dell'altro. $$ \vec{v}_1 = \lambda \cdot \vec{v}_2 \ \ \alpha \in K $$ I due vettori hanno la stessa direzione e si trovano sulla stessa retta.
  
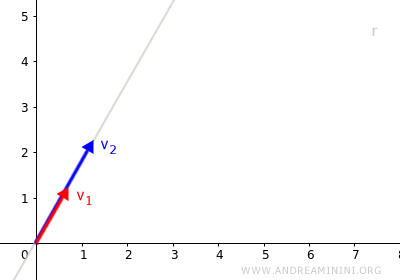
  Quindi, le combinazioni lineari dei due vettori sono dei vettori che risiedono sulla stessa retta di v₁ e v₂. $$ L(\vec{v}_1 , \vec{v}_2) = \{ \lambda_1 \vec{v}_1 + \lambda_2 \vec{v}_2 \ | \ \forall \ \lambda \in K \} $$
• Se i due vettori non sono paralleli
  In questo caso i due vettori sono linearmente indipendenti. Non posso scrivere un vettore come multiplo dell'altro $$ \vec{v}_1 \ne \lambda \cdot \vec{v}_2 \ \ \alpha \in K $$ I due vettori hanno direzioni diverse, ossia si trovano su retta differenti.
  
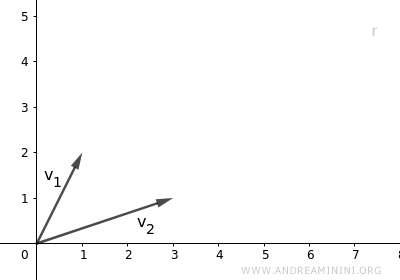
  Quindi, le combinazioni lineari dei due vettori sono i vettori che risiedono sullo stesso piano che contiene v₁ e v₂. $$ L(\vec{v}_1 , \vec{v}_2) = \{ \lambda_1 \vec{v}_1 + \lambda_2 \vec{v}_2 \ | \ \forall \ \lambda \in K \} $$

Esempio

Considero l'insieme dei vettori

$$ S = \{ v_1, v_2 \} $$

I vettori v₁ e v₂ sono

$$ v_1 = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$

$$ v_2 = \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$

Dal punto di vista geometrico i due vettori sono linearmente indipendenti nel piano perché non sono paralleli.

L'insieme di vettori appartiene allo spazio vettoriale V=R²

$$ S \subset V=R^2 $$

L'insieme L(S) è il più piccolo sottospazio vettoriale generato dai due vettori v₁ e v₂, ossia dalle loro combinazioni lineari

$$ L(S) = \lambda_1 \cdot \vec{v}_1 + \lambda_2 \vec{v}_2 $$

$$ L(S) = \lambda_1 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} + \lambda_2 \cdot \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$

Dove λ₁ e λ₂ sono due coefficienti reali qualsiasi.

Il sottospazio vettoriale L(S) è composto da tutti i vettori generati dalle combinazioni lineari dei vettori v₁ e v₂.

Nota. Prendendo λ₁=2 e λ₂=3 ottengo tramite la combinazione lineare il vettore v_n=(11,7) $$ \vec{v}_n= \lambda_1 \cdot \vec{v}_1 + \lambda_2 \vec{v}_2 $$ $$ \vec{v}_n = 2 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} + 3 \cdot \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$ $$ \vec{v}_n = \begin{pmatrix} 2 \cdot 1 \\ 2 \cdot 2 \end{pmatrix} + \begin{pmatrix} 3 \cdot 3 \\ 3 \cdot 1 \end{pmatrix} $$ $$ \vec{v}_n = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \begin{pmatrix} 9 \\ 3 \end{pmatrix} $$ $$ \vec{v}_n = \begin{pmatrix} 2+9 \\ 4+3 \end{pmatrix} $$ $$ \vec{v}_n = \begin{pmatrix} 11 \\ 7 \end{pmatrix} $$ Dal punto di vista geometrico

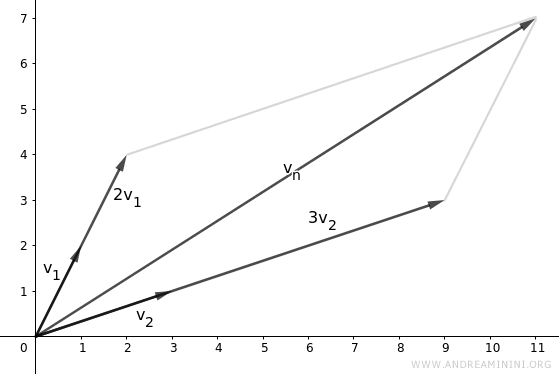
E così via.