Area del trapezio
L'area del trapezio si calcola moltiplicando l'altezza (h) per la media aritmetica delle lunghezze delle sue due basi (b1+b2)/2. $$ A = \frac{(b_1+b_2) \cdot h}{2} $$ Dove b1 è la base maggiore, b2 è la base minore, h è l'altezza del trapezio, ossia la distanza perpendicolare tra le due basi.
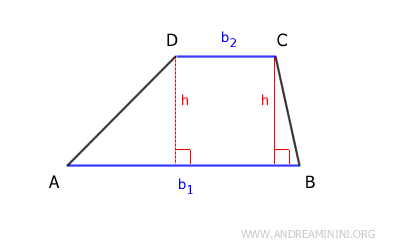
Il trapezio è una figura geometrica piana con quattro lati, di cui almeno due sono paralleli tra loro e vengono chiamati basi.
L'area del trapezio rappresenta la misura della superficie interna di questa figura.
Un esempio pratico
Supponiamo di avere un trapezio con una base maggiore di 8 cm, una base minore di 5 cm e un'altezza di 4 cm.
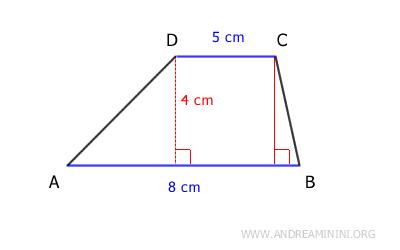
Utilizzando la formula:
$$ A = \frac{(8+5) \cdot 4}{2} $$
$$ A = \frac{13 \ cm \ \cdot 4 \ cm \ }{2} $$
$$ A = \frac{52 \ cm^2 }{2} $$
$$ A = 26 \ cm^2 $$
L'area del trapezio in questo esempio è di 26 cm^2.
La dimostrazione
Se traccio una linea perpendicolare (h) dalle estremità della base minore alla base maggiore del trapezio, ottengoo due triangoli rettangoli e un rettangolo al centro.
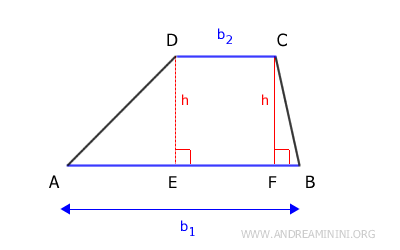
Quindi, posso considerare il trapezio come la somma di due triangoli (AED e BCF) e un rettangolo (EFCD).
La somma dell'area di queste tre figure è l'area del trapezio (A).
$$ A = \frac{ \overline{AE} \cdot h }{2} + \frac{ \overline{BF} \cdot h }{2} + h \cdot \overline{EF} $$
Dove AE·h/2 è l'area del primo triangolo, BF·h/2 è l'area del secondo triangolo mentre BF·h è l'area del rettangolo.
Metto in evidenza l'altezza (h).
$$ A = h \cdot ( \frac{ \ \overline{AE} }{2} + \frac{ \overline{BF} }{2} + \overline{EF} \ ) $$
$$ A = h \cdot ( \frac{ \ \overline{AE} + \overline{BF} + 2 \overline{EF} }{2} \ ) $$
Posso riscrivere 2EF=EF+CD
$$ A = h \cdot ( \frac{ \ \overline{AE} + \overline{BF} + \overline{EF} + \overline{CD} }{2} \ ) $$
La somma delle lunghezze dei segmenti AE+BF+EF=b1 è uguale alla base maggiore.
$$ A = h \cdot \frac{ ( b_1 + \overline{CD} ) }{2} $$
Sapendo che il segmento CD=b2 è la lunghezza della base minore.
$$ A = h \cdot \frac{ ( b_1 + b_2 ) }{2} $$
Il risultato finale è la formula che volevo dimostrare.
La dimostrazione alternativa
Considero un trapezio ABCD
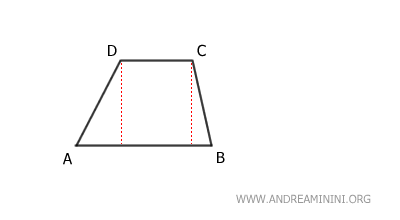
Prolungo la base maggiore AB aggiungendo all'estremo E un segmento congruente BE≅CD alla base minore.
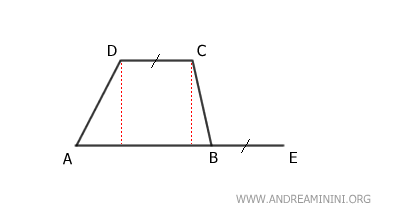
Poi faccio altrettanto sulla base minore CD, la prolungo all'estremo D aggiungendo un segmento CF=AB congruente con la base maggiore.
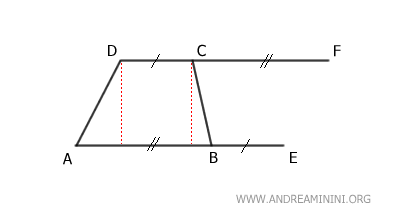
Traccio il segmento EF che unisce i punti E e F
Ora il trapezio si è trasformato in parallelogramma ADFE composto da due trapezi ABCD e BEFC.
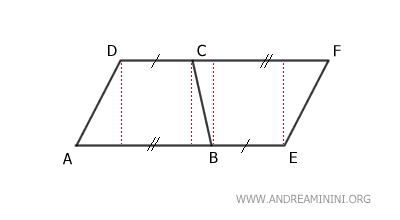
I trapezi ABCD≡BEFC sono congruenti perché hanno gli stessi lati nello stesso ordine.
Pertanto, il trapezio ABCD equivale alla metà del parallelogramma ADFE.
L'area del parallelogramma si calcola moltiplicando la base per l'altezza.
$$ A_p = \overline{AE} \cdot h $$
A sua volta il segmento AE è composto dai segmenti AB=b1 e BE=b2 ovvero dalle basi del trapezio iniziale
$$ A_p = ( \overline{AB} + \overline{BE} ) \cdot h $$
$$ A_p = ( b_1 + b_2 ) \cdot h $$
Sapendo che il trapezio è la metà del parallelogramma, deduco che l'area del trapezio è la metà dell'area del parallelogramma
$$ A = \frac{A_p}{2 } $$
$$ A = \frac{ ( b_1 + b_2 ) \cdot h}{2 } $$
In questo modo si dimostra la formula per calcolare l'area del trapezio.
E così via
