Le funzioni matematiche
Cos'è una funzione?
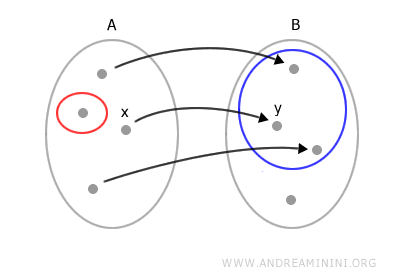
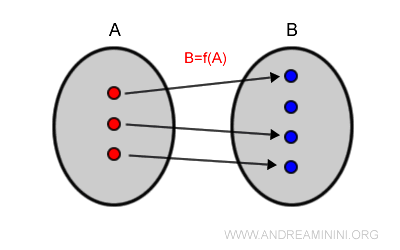
Una funzione è una relazione tra due insiemi A e B in cui a ogni elemento di A (insieme di partenza) è associato uno e un solo elemento di B (insieme di arrivo). $$ f:A \rightarrow B $$
Dove l'espressione "uno e un solo" vuol dire che per ogni elemento di A esiste un elemento di B associato ed è unico. Ecco un esempio di funzione.
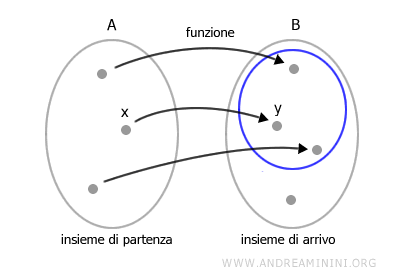
L'insieme di partenza A è detto dominio o insieme di definizione della funzione.
Dato un elemento x dell'insieme di partenza A esiste uno e un solo elemento y dell'insieme B, detto immagine di x tramite la funzione f.
$$ y = f(x) $$
Quest'ultima notazione si legge "y uguale a f di x"
A sua volta l'elemento x è detto controimmagine di y.
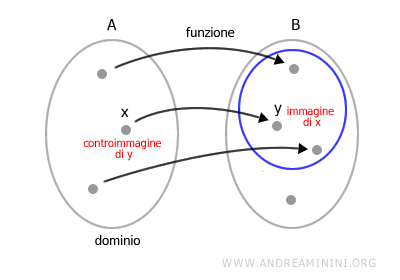
Non occorre che tutti gli elementi (y) di B siano associati ad un elemento (x) di A.
Il sottoinsieme C⊆B dell'insieme B composto da tutte le immagini y=f(x) degli elementi di A è detto codominio della funzione.
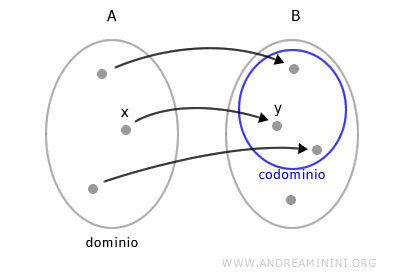
Nota. Il valore di y dipende dal valore di x. Per questa ragione y è detta variabile dipendente mentre x è detta variabile indipendente della funzione.
Per indicare una funzione si usa una lettera minuscola. Spesso f, g, h...
$$ f:A \rightarrow B $$
In alternativa, considerando x∈A e y∈B due elementi generici degli insiemi A e B posso anche scrivere
$$ f:x \longmapsto y $$
La funzione f è anche detta corrispondenza univoca perché a ogni elemento del dominio corrisponde un elemento del codominio.
Quando una relazione non è una funzione? Una relazione NON è una funzione se un elemento dell'insieme A è in relazione con più di un elemento dell'insieme B.
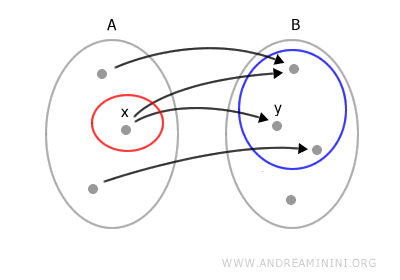
Una relazione non è una funzione se almeno un elemento dell'insieme A non è in relazione con nessun elemento dell'insieme B.
Il dominio della funzione
Il dominio della funzione è l'insieme dei valori della variabile indipendente x ammessi dalla funzione.
Ad esempio, questa funzione reale ammette tutti i valori reali trannte il numero zero x=0
$$ \frac{1}{x} $$
La divisione per zero è un'operazione indefinita in matematica.
Quindi, il dominio della funzione è l'insieme ristretto R-{0}
$$ R- \{0 \} $$
ossia l'insieme dei numeri reali R senza il numero zero.
Funzione in forma esplicita o in forma implicita
Una funzione matematica può essere scritta in forma esplicita oppure in forma implicita.
- Forma esplicita
La funzione in forma esplicita è nella forma y=f(x) $$ y = x+1 $$ - Forma implicita
La funzione in forma implicita è nella forma F(x;y)=0 $$ y-x-1 = 0 $$
Una funzione può essere vista anche come un insieme di coppie (x,y) con x∈A e y∈B in cui gli l'elemento x appare una sola volta.
$$ f:A \rightarrow B $$
Detto in altri termini, per ogni a∈A corrisponde tramite la funzione f() uno e un solo elemento b∈B.
$$ b = f(a) $$
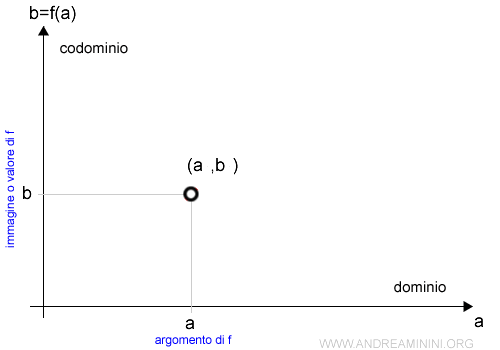
In una coppia (a,b) l'elemento a è detto argomento di f mentre l'elemento b è detto immagine di a mediante la funzione f ( o valore di f ).
$$ (a,b)_f = (a,f(a)) $$
Ogni coppia (a,b) è rappresentabile sul piano tramite il diagramma cartesiano ( rappresentazione cartesiana ).
L'insieme F delle coppie (a,b) della funzione f è detto grafico della funzione.
Il grafico della funzione è un sottoinsieme del prodotto cartesiano tra gli insiemi AxB.
$$ \{(a,f(a) | a \in A \} \subseteq AxB $$
Nota. Ovviamente, non tutti i sottoinsiemi di AxB sono funzioni. Per esserlo, ogni elemento a di A deve apparire una e una sola volta nelle coppie (a,b). Nei sottoinsiemi del prodotto cartesiano sono presenti anche altre relazioni che non sono funzioni.
Un esempio pratico di funzione
Esempio 1
Ecco un esempio di funzione f:R->R
$$ f(x)=x^2+1 $$
Per ogni elemento x dell'insieme dei numeri reali, c'è un'immagine f(x).
$$ f(0)= 0^2+1 = 1 \\ f(1)=1^2+1 = 2 \\ f(2) = 2^2+1=5 \\ \vdots $$
Esempio 2
La funzione può anche collegare insiemi diversi.
In questo caso, il dominio è l'insieme dei numeri reali e il codominio è l'insieme dei numeri interi.
$$ f:R \rightarrow Z $$
Ad esempio, la funzione f(x)=|x|.
$$ f(2.2)=|2.2|=2 \\ f(3.4)=|3.4|=3 \\ f(3.5)=|3.5|=3 \\ \vdots $$
Il grafico della funzione
L'elemento a del dominio della funzione compare una e una sola volta nelle coppie ordinate (a,b). L'elemento b, invece, può comparire anche più volte.
Posso quindi rappresentare il grafico della funzione f:A → B su un diagramma cartesiano.
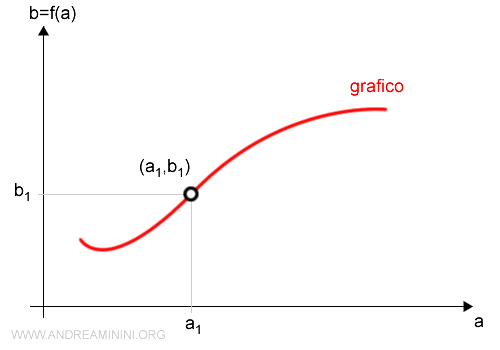
Sull'asse delle ascisse (x) indico gli elementi a di A del dominio, mentre sull'asse delle ordinate (y) gli elementi b di B del codominio.
Ogni punto del diagramma è un elemento del prodotto cartesiano AxB
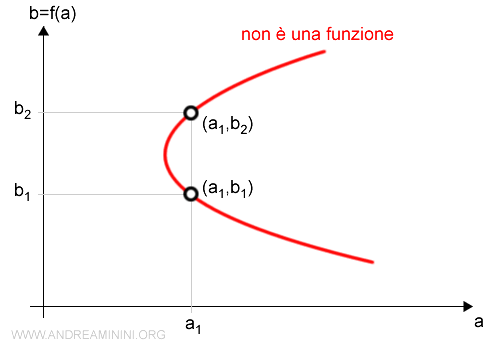
Tuttavia, soltanto le coppie (a,b) del grafico rosso appartengono alla funzione.
Nota. E' un'ulteriore dimostrazione che la funzione è un sottoinsieme del prodotto cartesiano AxB. Bisogna però ricordare che non tutti i sottoinsiemi di AxB sono funzioni. Ad esempio, questa figura non può essere un grafico perché gli elementi a compaiono più di una volta nelle coppie ordinate (a,b).
Il segno della funzione
Negli intervalli in cui la funzione è maggiore di zero y=f(x)>0 è detta positiva.
Viceversa, negli intervalli in cui la funzione è minore di zero y=f(x)<0 è detta negativa.
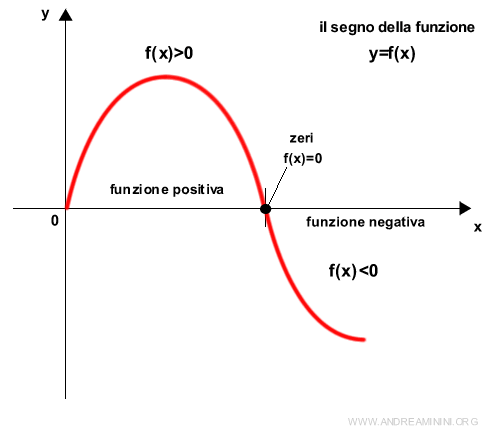
I punti in cui la funzione è nulla f(x)=0 sono detti zeri della funzione.
La positività e la negatività della funzione li determino algebricamente tramite lo studio del segno della funzione.
Nota. Le altre caratteristiche della funzione (es. crescenza, decrescenza, convessità, concavità, minimi, massimi, flessi, ecc), invece, li determino tramite lo studio della funzione usando gli strumenti dell'analisi matematica.
La classificazione delle funzioni
Le funzioni sono classificate a seconda delle operazioni matematiche contenute nell'espressione f(x)
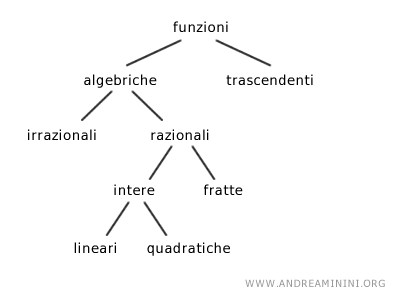
Ad esempio, sono funzioni algebriche quelle che contengono le quattro operazioni aritmetiche (addizione, sottrazione, moltiplicazione, divisione), l'elevamento a potenza e/o le radici.
Viceversa sono funzioni trascendenti quelle in cui la variabile indipendente x compare nell'argomento di una funzione trigonometrica, del logaritmo oppure in un esponenziale.
Esempio. Un esempio di funzione algebrica è la seguente $$ y=2x^3-x $$ Un esempio di funzione trascendente è $$ y=2x^3- \sin(x) $$
A loro volta le funzioni algebriche si dividono in irrazionali o razionali a seconda se la x si trova nell'argomento di un radicale oppure no.
Esempio. Un esempio di funzione irrazionale è la seguente $$ y=2x^3-\sqrt{x} $$ Un esempio di funzione razionale è $$ y=2x^3- x $$
Infine, le funzioni razionali sono dette intere o fratte se l'espressione è un polinomio o il quoziente di due polinomi.
Esempio. Un esempio di funzione intera è la seguente $$ y=2x^3-x $$ Un esempio di funzione fratta è $$ y= \frac{2x^3-2}{x^2+2x-5} $$
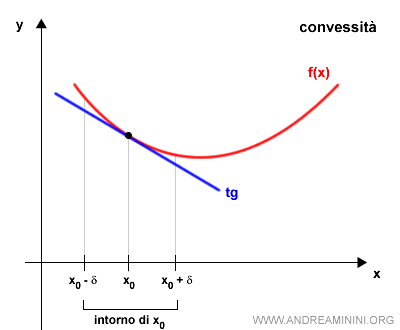
La funzione concava e convessa
In un intervallo [a,b] la funzione si dice
- convessa
se il grafico si trova al di sopra della retta tangente al grafico.
- concava
se il grafico si trova al di sotto della retta tangente al grafico.
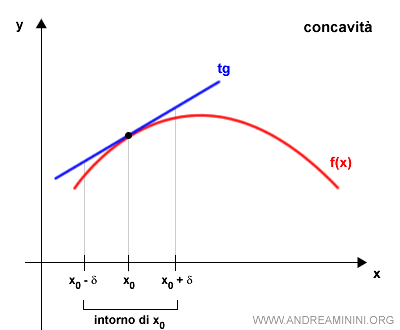
Una funzione può essere concava o convessa in tutto il suo dominio o soltanto in determinati intervalli.
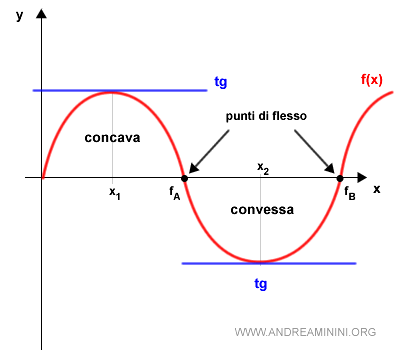
Nota. Oltre alla convessità e alla concavità, esistono anche funzioni costanti che non sono né concave, né convesse.

Inoltre, in appositi punti detti punti di flesso le funzioni potrebbero essere concave nell'intorno sinistro e convesse nell'intorno destro (o viceversa).
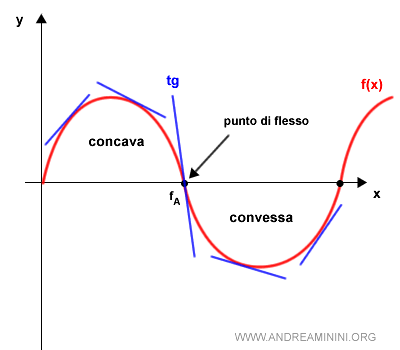
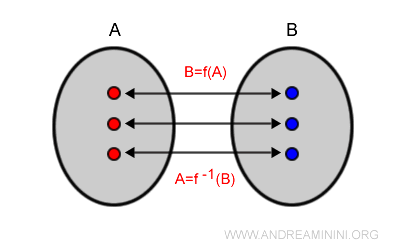
Immagine e controimmagine
L'immagine dell'insieme A (dominio) mediante la funzione f è l'insieme B (codominio).
$$ B = f(A) $$
La controimmagine ( o immagine inversa ) dell'insieme B rispetto alla funzione f è l'insieme A. E' una relazione inversa f-1 che collega ogni elemento dell'insieme B a uno e un solo elemento dell'insieme A.
$$ A = f^{-1}(B) $$
Nota. Tutte le relazioni hanno una relazione inversa. Tuttavia, non tutte le funzioni hanno una funzione inversa (f-1). Spesso la relazione inversa di una funzione f(x) non è una funzione perché l'elemento y del dominio f-1(y) compare più di una volta. Ad esempio la funzione f(x)=x2 non ha una funzione inversa. x=f-1(y) con y=4 è presente due volte perché nella funzione f(x) la y è uguale a 4 sia per x=2 e sia per x=-2. E così via.
La differenza tra funzione iniettiva, suriettiva e biettiva
Una funzione è iniettiva se ogni elemento di A (dominio) ha immagini distinte in B (codominio). $$ x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) $$
Esempio 1
La funzione y=x+2 è iniettiva perché a ogni elemento di x corrisponde uno e un solo valore di y.
Gli elementi x=2 e x=-2 hanno immagini distinite, y=4 e y=0.
Esempio 2
La funzione y=x2 invece non è iniettiva perché agli elementi di x corrispondono immagini uguali.
Gli elementi x=2 e x=-2 hanno la stessa immagine y=4.
La funzione è suriettiva ( o surgettiva ) se ogni elemento di B (codominio) ha almeno una controimmagine in A (dominio). $$ \forall \ b \in B \:\: \exists \:\: a \in A : f(a)=b $$
Esempio 1
La funzione y=x2 non è suriettiva perché gli elementi y<0 non hanno nessuna controimmagine x.
Esempio 2
La funzione y=x+1 è suriettiva perché ogni elemento y ha una controimmagine x.
La funzione è biettiva (o biunivoca) se è sia iniettiva che suriettiva.
Le funzioni biettive y=f(x) sono le uniche funzioni ad avere sempre una funzione inversa x=f-1(y).
Se la funzione è biettiva, la funzione composta con la sua funzione inversa è un'applicazione identica.
$$ f^{-1}(f(x)) = x $$
Nota. Un'applicazione è detta identica se f(x)=x.
La funzione composta
Date due funzioni f:A→B e g:B→C la funzione composta di f con g si indica $$ f \ o \ g:A \rightarrow C $$ oppure $$ F = f[g(x)]$$ dove f è detta funzione esterna mentre g è detta funzione interna.
Esempio
Ho due funzioni f(x) e g(x)
$$ f(x) = x+1 $$
$$ g(x) = 2x+3 $$
La funzione (g o f) è la seguente:
$$ g(f(x)) \\ g(x+1) \\ 2(x+1)+3 \\ 2x+5 $$
E così via.
- Il dominio
- Il codominio
- Gli zeri della funzione
- Le funzioni pari
- Le funzioni dispari
- La funzione segno
- La funzione crescente
- La funzione decrescente
- Le funzioni definite a tratti
- La funzione direttamente proporzionale
- La funzione inversamente proporzionale
- La funzione quadratica
- La funzione esponenziale
- La funzione logaritmica
- La funzione valore assoluto (o modulo)
- Le funzioni uniformemente continue
- Le funzioni sinusoidali
- Il teorema di Heine-Cantor
- Le funzioni lipschitziane
Funzioni a due variabili
