Funzione discontinua
Una funzione f(x) è discontinua in un punto x0 se il limite per x che tende a x0 non è uguale a f(x0). $$ \lim_{x \rightarrow x_0} f(x) \ne f(x_0) $$ Il punto x0 è detto punto di discontinuità.
Un esempio di funzione discontinua
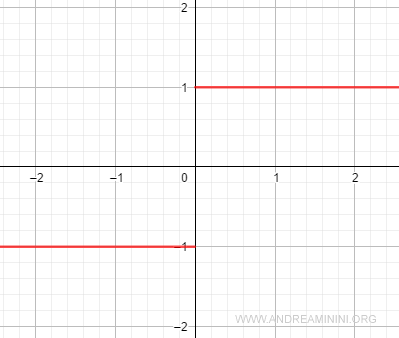
La discontinuità eliminabile e non eliminabile
- La discontinuità è detta discontinuità eliminabile se è possibile tracciare un prolungamento continuo per eliminarla.
- La discontinuità è detta discontinuità non eliminabile se non è possibile farlo.
Le cause della discontinuità
La discontinuità può verificarsi per diverse cause:
Discontinuità di prima specie
Nel punto x0 il limite destro non è uguale al limite sinistro della funzione. E' detta discontinuità di prima specie. $$ \lim_{x \rightarrow x_0^+} f(x) \ne \lim_{x \rightarrow x_0^-} f(x) $$
Nel punto x0 la funzione può essere definita o non definita.
Esempio
La funzione segno ha un punto di discontinuità in x0=0
$$ \frac{|x|}{x} $$
perché il limite destro e sinistro non coincidono
$$ \lim_{x \rightarrow 0^+} \frac{|x|}{x} = 1 $$
$$ \lim_{x \rightarrow 0^-} \frac{|x|}{x} = -1 $$
Ecco la rappresentazione grafica
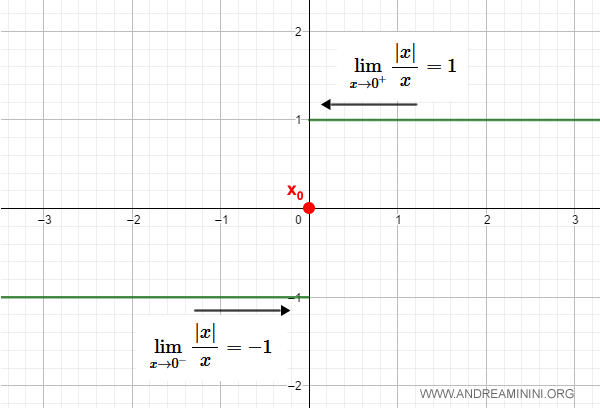
Nel punto x0 la funzione ha un salto da -1 a +1.
Discontinuità di seconda specie
Il limite destro e/o il limite sinistro è uguale a infinito oppure non esiste. E' detta discontinuità di seconda specie.
$$ \lim_{x \rightarrow x_0^±} f(x) \ne f(x_0) = \{ ±∞ , non \: esiste \} $$
Esempio
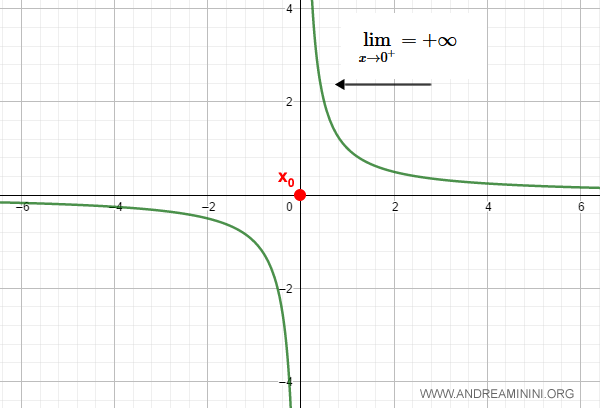
Questa funzione è discontinua in x0=0
$$ \frac{1}{x} $$
perché il limite destro è uguale a infinito.
$$ \lim_{x \rightarrow 0^+} = +∞ $$
Nota. In questo caso anche il limite sinistro è un infinito, per la precisione meno infinito. $$ \lim_{x \rightarrow 0^-} = -∞ $$ In ogni caso, per avere una discontinuità di seconda specie in un punto x0 è sufficiente che almeno uno dei due limiti destro o sinistro sia un infinito (±∞).
Ecco la rappresentazione grafica.
Discontinuità di terza specie ( o eliminabile )
Nel punto x0 il limite della funzione esiste ma non è uguale al valore della funzione f(x0). $$ \lim_{x \rightarrow x_0} f(x) \ne f(x_0) $$
E' detta discontinuità eliminabile perché si può attribuire un valore alla funzione in x0 per renderla continua anche nel punto x0 tramite un prolungamento per continuità.
E' una discontinuità che si presenta nelle funzioni a tratti
Esempio
Questa funzione ha una discontinuità della terza specie
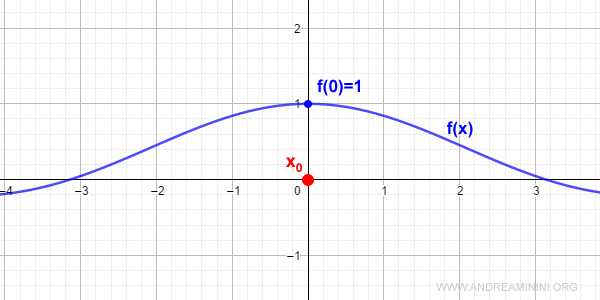
$$ f(x) = \frac{\sin x}{x} $$
Nel punto x0=0 la funzione non è definita ma il limite per x che tende a x0 esiste.
$$ \lim_{x \rightarrow 0} \frac{\sin x}{x} = 1 $$
Si tratta di un limite notevole.
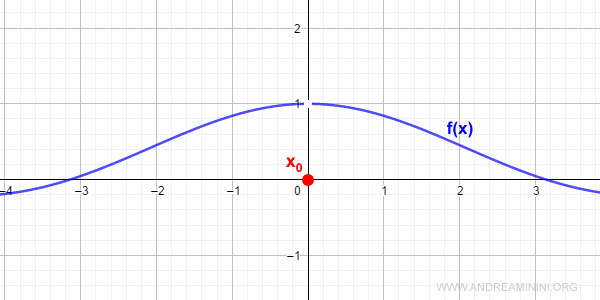
Per eliminare la discontinuità assegno al punto x0=0 il valore f(0)=1 tramite un prolungamento di continuità.
$$ f(x) = \begin{cases} \frac{\sin x}{x} \: se \: x \ne 0 \\ 1 \: se \: x=0 \end{cases} $$
In questo modo la discontinuità viene eliminata.
Esempio 2
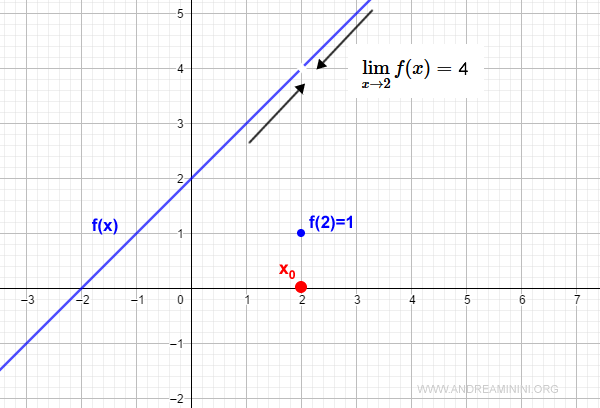
Prendo in considerazione questa funzione a tratti
$$ f(x) = \begin{cases} x+2 \: se \: x \ne 2 \\ 1 \: se \: x=2 \end{cases} $$
La funzione ha un punto di discontinuità nel punto x0=2.
Il limite per x che tende a x0=2 esiste.
$$ \lim_{x \rightarrow 2} f(x) = 4 $$
Pertanto, il limite destro e sinistro sono uguali.
Tuttavia, la funzione è uguale a uno in x0=2.
$$ f(2) = 1 $$
Quindi, il limite della funzione esiste in x0 ma la funzione ha un valore diverso.
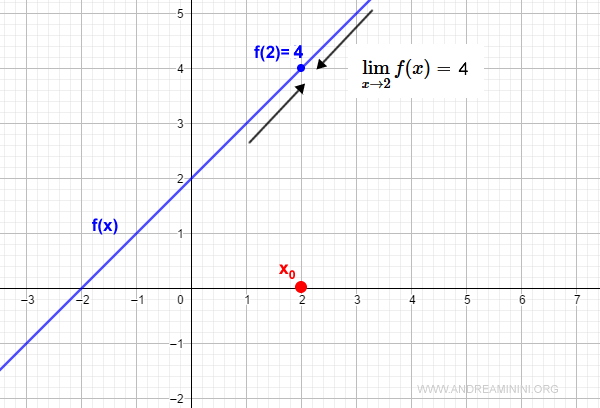
Per eliminare questo punto di discontinuità basta ridefinire la funzione con un prolungamento per continuità
$$ f(x) = \begin{cases} x+2 \: se \: x \ne 2 \\ 4 \: se \: x=2 \end{cases} $$
Il punto di discontinuità è stato eliminato.
E così via.
